Hexaederstumpf berechnen

Rechner und Formeln zur Berechnung des Hexaederstumpfs (Truncated Cube)

Hexaederstumpf Rechner

Der Hexaederstumpf

Ein Hexaederstumpf ist ein archimedischer Körper mit 14 Flächen: 6 regelmäßige Achtecke und 8 gleichseitige Dreiecke.

Bekannten Parameter eingeben
Welcher Parameter ist bekannt?
Wert des ausgewählten Parameters
Hexaederstumpf-Eigenschaften

Einfache Struktur: 24 Ecken, 36 Kanten, 14 Flächen

6 Achtecke 8 Dreiecke Archimedisch
Hexaederstumpf-Berechnungsergebnisse
Seitenlänge a:
Volumen V:
Oberfläche S:
Höhe h:
Umkugelradius rc:
Kantenradius rm:

Hexaederstumpf-Struktur

Ein Hexaederstumpf ist ein archimedischer Körper.
Er entsteht durch Abstumpfung eines Würfels.

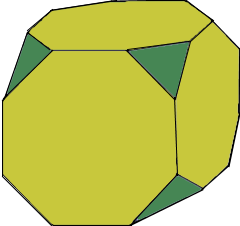
Hexaederstumpf

● 6 Achtecke ● 8 Dreiecke ● 24 Ecken


Was ist ein Hexaederstumpf?

Ein Hexaederstumpf (Truncated Cube) ist einer der 13 archimedischen Körper:

  • 14 Flächen: 6 regelmäßige Achtecke und 8 gleichseitige Dreiecke
  • 24 Ecken: Jede Ecke wird von 2 Achtecken und 1 Dreieck gebildet
  • 36 Kanten: Alle Kanten haben die gleiche Länge
  • Entstehung: Durch Abstumpfung eines regulären Würfels
  • Oktaedrische Symmetrie: Moderate Symmetriegruppe
  • Einfache Struktur: Weniger komplex als andere archimedische Körper

Geometrische Eigenschaften

Der Hexaederstumpf besitzt einzigartige geometrische Eigenschaften:

Flächenstruktur
  • 6 Achtecke: Von den ursprünglichen Würfelflächen
  • 8 Dreiecke: Durch die Abstumpfungs-Operation entstanden
  • Einheitliche Kanten: Alle 36 Kanten sind gleich lang
  • Vertex-Figur: Jede Ecke: 2 Achtecke + 1 Dreieck
Besondere Eigenschaften
  • Oktaedrische Symmetrie: 24 Symmetrieoperationen
  • √2-Konstante: Alle Formeln enthalten √2
  • Einfache Truncation: Direkte Ableitung vom Würfel
  • Konvexer Körper: Alle Innenwinkel < 180°

Mathematische Beziehungen

Der Hexaederstumpf folgt eleganten mathematischen Gesetzen:

Volumenberechnung
V = a³(21+14√2)/3

Das Volumen enthält die Quadratwurzel aus 2, charakteristisch für kubische Geometrie.

Oberflächenberechnung
S = 2a²(6+6√2+√3)

Die Oberfläche kombiniert die Flächen von 6 Achtecken und 8 Dreiecken.

Anwendungen des Hexaederstumpfs

Hexaederstümpfe finden sich in verschiedenen Bereichen:

Wissenschaft & Forschung
  • Kristallstrukturen und Mineralien
  • Molekulare Geometrie und Koordinationschemie
  • Packungsprobleme in der Mathematik
  • Strukturelle Festkörperphysik
Kunst & Design
  • Architektonische Strukturelemente
  • Skulpturen und Installationen
  • Schmuckdesign und Uhrengehäuse
  • Industriedesign und Produktgestaltung
Spiele & Unterhaltung
  • Spezielle Würfel und Gaming-Komponenten
  • Puzzle und mechanische Spielzeuge
  • 3D-Modellierung und CAD-Anwendungen
  • Lernspiele für Geometrie-Unterricht
Technik & Engineering
  • Maschinenbau und Strukturelemente
  • Druckbehälter und Tanks
  • Optische Komponenten und Prismen
  • Verpackungsindustrie und Container

Formeln für den Hexaederstumpf

Volumen V
\[V=\frac{a^3(21+14\sqrt{2})}{3}\]

Einfache Formel mit √2-Beziehungen

Oberfläche S
\[S= 2a^2(6+6\sqrt{2} +\sqrt{3})\]

Kombiniert Achteck- und Dreieckflächen

Höhe h
\[h=a(1+ \sqrt{2})\]

Höhe des truncated Cubes

Umkugelradius rc
\[r_c=\frac{a\sqrt{7+4\sqrt{2}}}{2}\]

Radius der umschreibenden Kugel

Kantenradius rm
\[r_m=\frac{a(2+ \sqrt{2})}{2}\]

Radius der Kugel durch Kantenmittelpunkte

√2-Konstante
\[\sqrt{2} \approx 1.4142135624\]

Fundamentale Konstante in allen Formeln

Rechenbeispiel für einen Hexaederstumpf

Gegeben
Seitenlänge a = 10

Gesucht: Alle Eigenschaften des Hexaederstumpfs

1. Konstante berechnen
\[\sqrt{2} = 1.4142136\] \[\sqrt{3} = 1.7320508\]

Fundamentale Konstanten bestimmen

2. Oberflächenberechnung
\[S = 2 \times 100 \times 15.464\] \[S = 3092.8\]

Oberfläche aus Seitenlänge

3. Volumen und Höhe
\[V = \frac{1000 \times 40.799}{3} = 13599.7\] \[h = 10 \times 2.414 = 24.14\]

Volumen und Höhe berechnen

4. Radien berechnen
\[r_c = 10 \times 1.778 = 17.78\] \[r_m = 10 \times 1.707 = 17.07\]

Umkugel- und Kantenradius

5. Vollständiger Hexaederstumpf
Seitenlänge a = 10.00 Oberfläche S = 3092.8
Volumen V = 13599.7 Höhe h = 24.14
Umkugelradius = 17.78 14 Flächen total

Ein eleganter archimedischer Körper mit einfacher √2-Geometrie

Der Hexaederstumpf: Eleganz der kubischen Truncation

Der Hexaederstumpf (englisch: Truncated Cube) ist der einfachste und zugänglichste der archimedischen Körper, der durch die systematische Abstumpfung eines Würfels entsteht. Mit nur 14 Flächen und einer klaren geometrischen Struktur bietet er einen idealen Einstieg in die Welt der archimedischen Polyeder und demonstriert eindrucksvoll, wie aus der Einfachheit des Würfels durch eine einzige Transformation eine neue, harmonische geometrische Form entstehen kann.

Die Truncation des Würfels

Der Hexaederstumpf entsteht durch eine präzise geometrische Operation:

  • Ausgangsform: Regulärer Hexaeder (Würfel) mit 6 quadratischen Flächen und 8 Ecken
  • Abstumpfung: Jede der 8 Ecken wird durch eine dreieckige Fläche ersetzt
  • Flächentransformation: Die 6 ursprünglichen Quadrate werden zu regelmäßigen Achtecken
  • Resultat: 8 neue gleichseitige Dreiecke + 6 regelmäßige Achtecke = 14 Flächen
  • Kantenlänge: Der Abstumpfungsgrad wird so gewählt, dass alle 36 Kanten gleich lang sind

Die √2-Konstante als geometrisches Prinzip

Im Gegensatz zu komplexeren archimedischen Körpern basiert der Hexaederstumpf auf der einfachen √2-Konstante:

Kubische Verwandtschaft

√2 ≈ 1.414 ist die fundamentale Konstante kubischer Geometrie - das Verhältnis der Raumdiagonale zur Kantenlänge eines Quadrats. Diese einfache Beziehung durchzieht alle Formeln des Hexaederstumpfs.

Oktaedrische Symmetrie

Mit 24 Symmetrieoperationen besitzt der Hexaederstumpf die gleiche Symmetriegruppe O_h wie der ursprüngliche Würfel. Diese moderate Komplexität macht ihn mathematisch zugänglich.

Einfache Arithmetik

Die Formeln enthalten nur √2 und √3, keine komplexen Ausdrücke wie den goldenen Schnitt. Dies macht Berechnungen praktikabel und die Geometrie verständlich.

Konstruktive Einfachheit

Die exakte Konstruktion ist mit klassischen geometrischen Methoden möglich, da √2 konstruierbar ist. Dies unterscheidet ihn von komplexeren archimedischen Körpern.

Strukturelle Eigenschaften und Anwendungen

Der Hexaederstumpf zeigt bemerkenswerte strukturelle Eigenschaften:

Flächengeometrie

Die 6 Achtecke haben Innenwinkel von 135°, die 8 Dreiecke sind perfekt gleichseitig mit 60°-Winkeln. An jeder Ecke treffen zwei Achtecke und ein Dreieck zusammen (8.8.3).

Strukturelle Stabilität

Die Kombination aus Dreiecken und Achtecken verleiht optimale strukturelle Eigenschaften. Die Form ist selbsttragend und unter Belastung stabil.

Duale Beziehungen

Das duale Polyeder zum Hexaederstumpf ist das Triakis-Oktaeder, ein katalanischer Körper mit 24 unregelmäßigen dreieckigen Flächen.

Praktische Vorteile

Die moderate Anzahl von Flächen (14) macht ihn für praktische Anwendungen ideal - komplex genug für Interesse, einfach genug für Umsetzung.

Moderne Anwendungen und Technologie

Der Hexaederstumpf findet vielfältige praktische Anwendungen:

  • Verpackungsindustrie: Optimale Raumausnutzung bei Container-Design
  • Architektur: Strukturelemente und Dachkonstruktionen
  • Maschinenbau: Druckbehälter und Tanks mit optimaler Spannungsverteilung
  • Kristallographie: Bestimmte Kristallsysteme zeigen diese Geometrie
  • Optik: Prismengeometrie und optische Komponenten
  • 3D-Druck: Einfache Herstellung durch wenige Stützstrukturen
  • Spielindustrie: Würfel und Gaming-Komponenten
  • Bildung: Lernmodelle für Geometrie-Unterricht

Konstruktion und Herstellung

Die praktische Umsetzung des Hexaederstumpfs ist relativ einfach:

Traditionelle Konstruktion

Mit Zirkel und Lineal exakt konstruierbar. Handwerker können ihn mit einfachen geometrischen Kenntnissen herstellen. Die √2-Beziehungen sind praktisch umsetzbar.

Moderne Fertigung

CAD-Software berechnet automatisch alle Winkel. 3D-Druck ist problemlos möglich. CNC-Fertigung erzeugt präzise Oberflächen ohne komplexe Programmierung.

Materialeffizienz

Optimales Verhältnis von Material zu Festigkeit. Weniger Verschnitt als bei komplexeren Formen. Kosteneffiziente Produktion auch in kleineren Stückzahlen.

Qualitätskontrolle

Einfache Überprüfung der geometrischen Genauigkeit. Toleranzen sind großzügiger als bei komplexeren Polyedern. Robust gegen kleine Fertigungsabweichungen.

Zusammenfassung

Der Hexaederstumpf verkörpert geometrische Eleganz in ihrer zugänglichsten Form. Als direkter Nachkomme des Würfels behält er dessen strukturelle Klarheit, während er durch die Truncation neue ästhetische und funktionale Dimensionen gewinnt. Seine 14 Flächen, gesteuert durch die einfache √2-Konstante, machen ihn zum idealen Einstieg in die archimedische Geometrie. Von praktischen Anwendungen in der Industrie bis zu pädagogischen Zwecken in der Bildung - der Hexaederstumpf demonstriert, dass mathematische Schönheit nicht immer Komplexität erfordert. In einer Zeit zunehmender geometrischer Sophistikation bleibt er ein beruhigendes Beispiel dafür, dass elegante Lösungen oft in der intelligenten Transformation einfacher Grundformen zu finden sind. Seine zeitlose Ästhetik und praktische Anwendbarkeit machen ihn zu einem dauerhaften Favoriten unter Mathematikern, Ingenieuren und Designern gleichermaßen.

Abgeschrägtes Dodekaeder • Abgeschrägtes Hexaeder • Dodekaederstumpf • Hexaederstumpf • Ikosidodekaeder • Ikosaederstumpf • Ikosidodekaederstumpf • Kuboktaeder • Kuboktaederstumpf • Oktaederstumpf • Rhombenikosidodekaeder • Rhombenkuboktaeder • Tetraederstumpf