Kuboktaeder berechnen

Rechner und Formeln zur Berechnung des Kuboktaeders (Cuboctahedron)

Kuboktaeder Rechner

Das Kuboktaeder

Ein Kuboktaeder ist ein gleichmäßiger Körper mit 14 Flächen: 8 gleichseitige Dreiecke und 6 Quadrate - die perfekte Verschmelzung von Würfel und Oktaeder.

Bekannten Parameter eingeben
Welcher Parameter ist bekannt?
Wert des ausgewählten Parameters
Kuboktaeder-Eigenschaften

Duale Natur: 12 Ecken, 24 Kanten, 14 Flächen

8 Dreiecke 6 Quadrate Würfel+Oktaeder
Kuboktaeder-Berechnungsergebnisse
Seitenlänge a:
Volumen V:
Oberfläche S:
Umkugelradius rc:
Kantenradius rm:

Kuboktaeder-Struktur

Ein Kuboktaeder vereint Würfel und Oktaeder.
Perfekte Balance zwischen kubischen und oktaedrischen Formen.

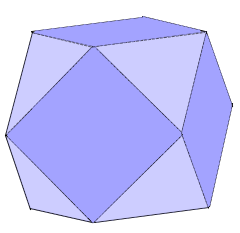
Kuboktaeder

● 8 Dreiecke ● 6 Quadrate ● 12 Ecken

Kuboktaeder Radius

Was ist ein Kuboktaeder?

Ein Kuboktaeder (Cuboctahedron) ist ein einzigartiger gleichmäßiger Polyeder:

  • 14 Flächen: 8 gleichseitige Dreiecke und 6 Quadrate
  • 12 Ecken: Jede Ecke wird von 2 Dreiecken und 2 Quadraten gebildet
  • 24 Kanten: Alle Kanten haben die gleiche Länge
  • Duale Natur: Vereint Würfel- und Oktaeder-Eigenschaften
  • Einfache Formeln: Elegant mit √2 und √3
  • Perfekte Balance: Optimales Verhältnis von Ecken, Kanten und Flächen

Geometrische Eigenschaften

Das Kuboktaeder besitzt harmonische geometrische Eigenschaften:

Flächenstruktur
  • 8 Dreiecke: Gleichseitige dreieckige Flächen
  • 6 Quadrate: Regelmäßige viereckige Flächen
  • Einheitliche Kanten: Alle 24 Kanten sind gleich lang
  • Vertex-Figur: Jede Ecke: 2 Dreiecke + 2 Quadrate
Besondere Eigenschaften
  • Oktaedrische Symmetrie: 24 Symmetrieoperationen
  • Einfache Konstanten: Nur √2 und √3 in Formeln
  • Radius-Gleichheit: r_c = a (bemerkenswerte Eigenschaft)
  • Duale Beziehung: Selbst-dual mit rhombischem Dodekaeder

Mathematische Beziehungen

Das Kuboktaeder folgt eleganten mathematischen Gesetzen:

Volumenberechnung
V = 5√2a³/3

Einfache Formel mit √2, charakteristisch für kubische Geometrie.

Oberflächenberechnung
S = 2a²(3+√3)

Die Oberfläche kombiniert die Flächen von Dreiecken und Quadraten.

Anwendungen des Kuboktaeders

Kuboktaeder finden sich in verschiedenen Bereichen:

Wissenschaft & Forschung
  • Kristallstrukturen und Koordinationsgeometrie
  • Molekulare Käfigverbindungen
  • Packungsprobleme in der Mathematik
  • Festkörperphysik und Materialwissenschaft
Kunst & Design
  • Architektonische Strukturelemente
  • Skulpturen und moderne Kunst
  • Schmuckdesign und Lampenschirme
  • Industriedesign und Produktgestaltung
Spiele & Unterhaltung
  • Spezielle Würfel und Gaming-Komponenten
  • Puzzle und mechanische Spielzeuge
  • 3D-Modellierung und CAD-Anwendungen
  • Bildungs- und Lernspiele
Technik & Engineering
  • Maschinenbau und Strukturelemente
  • Robotik und mechanische Systeme
  • Optische Komponenten und Prismen
  • Verpackungsindustrie und Container

Formeln für das Kuboktaeder

Volumen V
\[V=\frac{5\sqrt{2}a^3}{3}\]

Einfache Formel mit √2-Beziehungen

Oberfläche S
\[S= 2a^2(3+\sqrt{3})\]

Kombiniert Dreiecks- und Quadratflächen

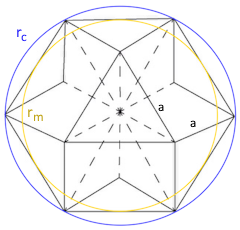
Umkugelradius rc
\[r_c=a\]

Bemerkenswert: Radius gleich Kantenlänge!

Kantenradius rm
\[r_m=\frac{a\sqrt{3}}{2}\]

Radius der Kugel durch Kantenmittelpunkte

√2-Konstante
\[\sqrt{2} \approx 1.4142135624\]

Fundamentale Konstante in Volumenformel

√3-Konstante
\[\sqrt{3} \approx 1.7320508076\]

Fundamentale Konstante in Oberflächenformel

Rechenbeispiel für ein Kuboktaeder

Gegeben
Seitenlänge a = 10

Gesucht: Alle Eigenschaften des Kuboktaeders

1. Konstanten berechnen
\[\sqrt{2} = 1.4142136\] \[\sqrt{3} = 1.7320508\]

Fundamentale Konstanten bestimmen

2. Oberflächenberechnung
\[S = 2 \times 100 \times 4.732\] \[S = 946.4\]

Oberfläche aus Seitenlänge

3. Volumenberechnung
\[V = \frac{5 \times 1.414 \times 1000}{3}\] \[V = 2357.0\]

Volumen mit √2-Formel

4. Radien berechnen
\[r_c = a = 10.00\] \[r_m = 10 \times 0.866 = 8.66\]

Bemerkenswert: r_c = a

5. Vollständiges Kuboktaeder
Seitenlänge a = 10.00 Oberfläche S = 946.4
Volumen V = 2357.0 Umkugelradius = 10.00
Kantenradius = 8.66 14 Flächen total

Ein eleganter Polyeder mit perfekter Balance zwischen Würfel und Oktaeder

Das Kuboktaeder: Harmonie zwischen Würfel und Oktaeder

Das Kuboktaeder (englisch: Cuboctahedron) steht als faszinierendes Beispiel für geometrische Harmonie und Ausgewogenheit. Als einer der einfachsten und elegantesten archimedischen Körper verkörpert es die perfekte Verschmelzung zwischen den beiden dualen platonischen Körpern - dem Würfel und dem Oktaeder. Mit nur 14 Flächen und bemerkenswert einfachen mathematischen Beziehungen ist es sowohl für Anfänger als auch für Experten ein faszinierendes Studienobjekt der Polyeder-Geometrie.

Die Dualität von Würfel und Oktaeder

Das Kuboktaeder entsteht durch eine bemerkenswerte geometrische Operation:

  • Kantenstumpfung: Gleichmäßiges Abstumpfen aller Kanten eines Würfels oder Oktaeders
  • Duale Entstehung: Kann sowohl vom Würfel als auch vom Oktaeder abgeleitet werden
  • Symmetrieerhaltung: Behält die oktaedrische Symmetriegruppe O_h bei
  • Flächenverteilung: 8 Dreiecke (vom Oktaeder) + 6 Quadrate (vom Würfel)
  • Vertex-Konfiguration: (3.4.3.4) - alternierend Dreiecke und Quadrate
  • Perfekte Balance: Keine der beiden Ausgangsformen dominiert

Mathematische Eleganz und Einfachheit

Das Kuboktaeder besticht durch seine mathematische Klarheit:

Einfache Konstanten

Im Gegensatz zu komplexeren archimedischen Körpern benötigt das Kuboktaeder nur die einfachen Wurzeln √2 und √3. Diese Klarheit macht es ideal für Berechnungen und Konstruktionen.

Bemerkenswerte Radius-Eigenschaft

Die Eigenschaft r_c = a (Umkugelradius gleich Kantenlänge) ist einzigartig unter den archimedischen Körpern und macht das Kuboktaeder besonders merkwürdig und erinnerungswert.

Oktaedrische Symmetrie

Mit 24 Symmetrieoperationen besitzt das Kuboktaeder die gleiche Symmetriegruppe wie Würfel und Oktaeder, was seine Rolle als Vermittler zwischen diesen Formen unterstreicht.

Konstruktive Zugänglichkeit

Die Konstruktion mit Zirkel und Lineal ist möglich, da alle benötigten Konstanten (√2, √3) klassisch konstruierbar sind. Dies macht es ideal für geometrische Studien.

Strukturelle Eigenschaften und Anwendungen

Das Kuboktaeder zeigt vielseitige strukturelle Eigenschaften:

Duales Polyeder

Das duale Polyeder zum Kuboktaeder ist das rhombische Dodekaeder mit 12 rhombischen Flächen. Diese Dualität verbindet gleichmäßige und katalanische Körper auf natürliche Weise.

Strukturelle Stabilität

Die Kombination aus Dreiecken und Quadraten verleiht optimale strukturelle Eigenschaften. Die Form ist selbsttragend und unter Belastung stabil.

Euler-Charakteristik

Mit V = 12, E = 24, F = 14 erfüllt es perfekt Eulers Polyederformel: V - E + F = 2. Die Zahlen stehen in harmonischen Verhältnissen zueinander.

Praktische Umsetzung

Die moderate Anzahl von Flächen (14) macht es für praktische Anwendungen ideal - komplex genug für Interesse, einfach genug für Umsetzung.

Moderne Anwendungen und Relevanz

Das Kuboktaeder findet vielfältige praktische Anwendungen:

  • Kristallographie: Koordinationspolyeder in Kristallstrukturen
  • Architektur: Strukturelemente und Raumunterteilungen
  • Molekularchemie: Käfigverbindungen und Koordinationskomplexe
  • Maschinenbau: Strukturelemente und mechanische Verbindungen
  • Kunst und Design: Skulpturen, Lampen und dekorative Objekte
  • Bildung: Ideales Lernmodell für Polyeder-Geometrie
  • 3D-Druck: Einfache Herstellung durch wenige Stützstrukturen
  • Robotik: Gelenkverbindungen und mechanische Systeme

Historische und kulturelle Bedeutung

Das Kuboktaeder hat eine reiche historische Tradition:

Antike Wurzeln

Bereits von den antiken Griechen studiert, verkörpert es das Ideal der geometrischen Harmonie. Es demonstriert, wie aus der Dualität Einheit entstehen kann.

Pädagogischer Wert

Als Einstieg in die archimedische Geometrie ist es unübertroffen. Seine Einfachheit ermöglicht das Verständnis komplexer Konzepte ohne überwältigende Mathematik.

Moderne Renaissance

In der zeitgenössischen Kunst und Architektur erlebt das Kuboktaeder eine Renaissance. Designer schätzen seine klaren Linien und harmonischen Proportionen.

Symbolische Bedeutung

Es steht symbolisch für Balance und Harmonie - die Vereinigung scheinbar gegensätzlicher Elemente zu einer höheren Einheit.

Zusammenfassung

Das Kuboktaeder steht als leuchtendes Beispiel für geometrische Eleganz und mathematische Klarheit. Als perfekte Synthese zwischen Würfel und Oktaeder verkörpert es die Idee, dass wahre Schönheit oft in der Balance zwischen Gegensätzen liegt. Seine 14 Flächen, gesteuert durch die einfachen Konstanten √2 und √3, machen es sowohl für Anfänger als auch für Experten zu einem faszinierenden Studienobjekt. Von antiken philosophischen Betrachtungen bis zu modernen technischen Anwendungen bleibt das Kuboktaeder ein zeitloses Symbol für die Kraft geometrischer Harmonie. In einer Zeit zunehmender Komplexität erinnert es uns daran, dass die elegantesten Lösungen oft in der intelligenten Vereinfachung und dem Finden der Balance zwischen scheinbar widersprüchlichen Elementen zu finden sind. Als Brücke zwischen den platonischen Körpern repräsentiert es die Quintessenz archimedischer Geometrie.

Abgeschrägtes Dodekaeder • Abgeschrägtes Hexaeder • Dodekaederstumpf • Hexaederstumpf • Ikosidodekaeder • Ikosaederstumpf • Ikosidodekaederstumpf • Kuboktaeder • Kuboktaederstumpf • Oktaederstumpf • Rhombenikosidodekaeder • Rhombenkuboktaeder • Tetraederstumpf