Tetraederstumpf berechnen
Onlinerechner zur Berechnung von Volumen und Oberfläche eines Tetraederstumpf
Tetraederstumpf Rechner
Der Tetraederstumpf
Ein Tetraederstumpf ist ein Archimedischer Körper, der durch Abschneiden der Ecken eines Tetraeders entsteht.
Tetraederstumpf-Struktur
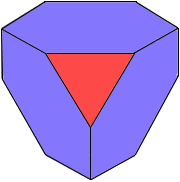
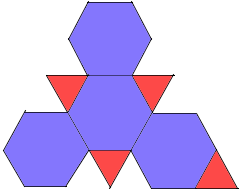
Ein Tetraederstumpf entsteht durch Abschneiden der Ecken.
Er besteht aus 4 gleichseitigen Dreiecken und 4 regelmäßigen Sechsecken.
|
|
Was ist ein Tetraederstumpf?
Ein Tetraederstumpf ist ein besonderer Archimedischer Körper:
- Entstehung: Durch Abschneiden der Ecken eines regelmäßigen Tetraeders
- Flächen: 4 gleichseitige Dreiecke + 4 regelmäßige Sechsecke
- Eigenschaften: Alle Kanten sind gleich lang
- Ecken: 12 identische Ecken
- Kanten: 18 identische Kanten
- Symmetrie: Tetraedrische Symmetriegruppe
Geometrische Eigenschaften des Tetraederstumpf
Der Tetraederstumpf besitzt interessante geometrische Eigenschaften:
Grundparameter
- Seitenlänge (a): Kantenlänge aller 18 Kanten
- Flächen: 8 reguläre Polygone (4 Dreiecke + 4 Sechsecke)
- Euler-Charakteristik: V - E + F = 12 - 18 + 8 = 2
- Duale Form: Triakis-Tetraeder
Besondere Eigenschaften
- Archimedischer Körper: Alle Ecken sind kongruent
- Vertex-Figur: (3.6.6) - Ein Dreieck und zwei Sechsecke
- Tetraedrische Symmetrie: 24 Symmetrieoperationen
- Truncation: Entsteht durch gleichmäßige Eckenabschrägung
Mathematische Beziehungen
Der Tetraederstumpf folgt präzisen mathematischen Gesetzen:
Volumenberechnung
Das Volumen wächst kubisch mit der Seitenlänge. Der Faktor 23√2/12 ≈ 2.71 ist charakteristisch.
Oberflächenberechnung
Die Oberfläche berücksichtigt Dreiecks- und Sechseckflächen. √3 stammt aus den regelmäßigen Polygonen.
Anwendungen des Tetraederstumpf
Tetraederstümpfe finden Anwendung in verschiedenen Bereichen:
Kristallographie & Chemie
- Molekülstrukturen und Koordinationsgeometrie
- Clusterverbindungen und Käfigmoleküle
- Kristalline Defektstrukturen
- Nanomaterialien und Fullerene
Architektur & Design
- Geodätische Strukturen und Raumfachwerke
- Skulpturale Architekturelemente
- Modulare Bausysteme
- Dekorative Geometrie und Kunst
Mathematik & Informatik
- Graphentheorie und Netzwerktopologie
- 3D-Modellierung und CAD-Systeme
- Finite-Elemente-Methoden
- Symmetriegruppen und Gruppentheorie
Spiele & Bildung
- Geometrische Puzzles und Lernspiele
- Lehrmodelle für Stereometrie
- Ungewöhnliche Würfelformen
- Virtual Reality und 3D-Visualisierung
Formeln für den Tetraederstumpf
Volumen V
Volumen in Abhängigkeit der Seitenlänge a
Oberfläche S
Gesamtoberfläche aller 8 Flächen
Umkugelradius rc
Radius der umschreibenden Kugel
Kantenradius rm
Radius der Kugel, die alle Kanten berührt
Seitenlänge a (Umkehrformeln)
aus Volumen
aus Oberfläche
aus Umkugelradius
aus Kantenradius
Seitenlänge aus anderen Parametern berechnen
Rechenbeispiel für einen Tetraederstumpf
Gegeben
Gesucht: Alle Eigenschaften des Tetraederstumpf
1. Volumenberechnung
Das Volumen beträgt etwa 1386 Kubikeinheiten
2. Oberflächenberechnung
Die Oberfläche beträgt etwa 775 Flächeneinheiten
3. Umkugelradius
Umkugelradius beträgt etwa 9.38
4. Kantenradius
Kantenradius beträgt etwa 8.48
5. Vollständiger Tetraederstumpf
Ein perfekter Archimedischer Körper mit allen berechneten Eigenschaften
Der Tetraederstumpf: Geometrische Eleganz durch Truncation
Der Tetraederstumpf (oder truncated tetrahedron) ist ein faszinierender Vertreter der Archimedischen Körper und entsteht durch systematische Abschrägung der Ecken eines regelmäßigen Tetraeders. Diese elegante Transformation verwandelt den einfachsten platonischen Körper in eine komplexere, aber harmonische geometrische Form.
Entstehung und charakteristische Eigenschaften
Der Tetraederstumpf entsteht durch einen präzisen geometrischen Prozess:
- Truncation-Prozess: Gleichmäßiges Abschneiden aller vier Ecken eines regelmäßigen Tetraeders
- Optimale Proportionen: Die Abschrägung erfolgt so, dass alle resultierenden Kanten gleich lang sind
- Flächentransformation: Die ursprünglichen Dreiecksflächen schrumpfen, neue Sechseckflächen entstehen
- Topologische Struktur: 8 Flächen, 18 Kanten, 12 Ecken (Euler: V-E+F = 12-18+8 = 2)
- Symmetrieerhaltung: Behält die tetraedrische Symmetriegruppe Td
- Dual-Körper: Der Triakis-Tetraeder ist sein dualer Polyeder
Historische Entwicklung und mathematische Bedeutung
Antike Geometrie
Obwohl die Archimedischen Körper nach Archimedes benannt sind, wurden Truncation-Verfahren bereits in der antiken Geometrie studiert. Der Tetraederstumpf repräsentiert den einfachsten Fall dieser Transformation.
Renaissancezeit
Künstler und Mathematiker der Renaissance wie Dürer und Pacioli studierten diese Körper intensiv. Der Tetraederstumpf erscheint in geometrischen Traktaten dieser Zeit.
Moderne Kristallographie
Im 19. und 20. Jahrhundert erkannte man die Bedeutung für Kristallstrukturen. Viele Mineralien zeigen tetraederstumpf-ähnliche Formen.
Zeitgenössische Anwendungen
Heute findet der Tetraederstumpf Anwendung in Nanotechnologie, Molekulardesign und moderner Architektur als optimale Strukturform.
Konstruktion und geometrische Beziehungen
Der Tetraederstumpf kann auf verschiedene Weise konstruiert und verstanden werden:
Konstruktion durch Truncation
Schneidet man von einem regelmäßigen Tetraeder an jeder Ecke eine kleinere Tetraederkappe ab, so dass die Schnittflächen regelmäßige Sechsecke werden, entsteht der Tetraederstumpf.
Koordinatengeometrie
Die Eckpunkte können systematisch durch Abschneiden der Tetraederecken bei (±1,±1,±1) mit geeigneten Schnittebenen konstruiert werden.
Verwandte Polyeder
Als Mitglied der Familie der gestumpften platonischen Körper steht er in Beziehung zu anderen Archimedischen Körpern wie dem Hexaederstumpf und Oktaederstumpf.
Dualitätsbeziehung
Der duale Triakis-Tetraeder besitzt dreieckige Flächen und zeigt die elegante Beziehung zwischen Ecken und Flächen in der Polyedertheorie.
Wissenschaftliche und technische Anwendungen
Die praktische Bedeutung des Tetraederstumpf reicht weit über die reine Geometrie hinaus:
- Molekularchemie: Käfigverbindungen und Clusterstrukturen in der anorganischen Chemie
- Kristallographie: Zwillingsstrukturen und Domänenbildung in Kristallen
- Materialwissenschaft: Nanopartikel und selbstorganisierende Strukturen
- Strukturmechanik: Optimale Raumfachwerke und geodätische Konstruktionen
- Computergrafik: Effiziente 3D-Modellierung und Finite-Elemente-Netze
- Spieltheorie: Ungewöhnliche Würfelformen für Strategiespiele
- Robotik: Optimale Greifstrukturen und modulare Robotersysteme
Besondere mathematische Eigenschaften
Numerische Eleganz
Die Formel für das Volumen V = (23√2/12)a³ ≈ 2.71a³ zeigt eine bemerkenswerte Verbindung zur Quadratwurzel aus 2, die auch in anderen tetraedrischen Strukturen auftritt.
Oberflächenoptimierung
Der Faktor 7√3 in der Oberflächenformel reflektiert die optimale Balance zwischen dreieckigen und sechseckigen Flächen für minimale Oberflächenenergie.
Symmetrieerhaltung
Trotz der Truncation bleibt die volle tetraedrische Symmetrie erhalten - ein Zeichen für die geometrische Perfektion dieser Transformation.
Goldener Schnitt
Die Proportionen des Tetraederstumpf stehen in interessanten Beziehungen zu irrationalen Zahlen und harmonischen Verhältnissen der klassischen Geometrie.
Physikalische und biologische Relevanz
Minimalprinzipien
Die Form des Tetraederstumpf tritt in der Natur auf, wenn Systeme ihre Oberflächenenergie minimieren müssen, etwa bei Seifenblasen-Clustern oder Zellstrukturen.
Packungsprobleme
In der statistischen Mechanik sind tetraederstumpf-ähnliche Formen relevant für optimale Packungen und Phasenübergänge in kolloidalen Systemen.
Biophysik
Proteinstrukturen und virale Kapsiden zeigen manchmal tetraederstumpf-ähnliche Symmetrien, besonders bei Selbstorganisationsprozessen.
Strömungsmechanik
Die Form ist aerodynamisch interessant und findet Anwendung in der Optimierung von Strömungswiderständen und Turbulenzmustern.
Zusammenfassung
Der Tetraederstumpf verkörpert die elegante Schönheit geometrischer Transformation. Als einfachster Vertreter der gestumpften platonischen Körper zeigt er, wie durch systematische Modifikation neue Formen mit faszinierenden Eigenschaften entstehen. Seine mathematischen Formeln mit √2 und √3 verbinden ihn mit fundamentalen geometrischen Konstanten, während seine Symmetrieeigenschaften die Harmonie der tetraedrischen Gruppe bewahren. Von der antiken Geometrie bis zur modernen Nanotechnologie inspiriert dieser Polyeder Wissenschaftler und Ingenieure. Als Brücke zwischen dem einfachen Tetraeder und komplexeren Archimedischen Körpern demonstriert der Tetraederstumpf die kraftvolle Idee der Truncation - ein fundamentales Prinzip, das in Natur, Technik und Kunst gleichermaßen Anwendung findet. Seine optimalen Eigenschaften bezüglich Oberfläche-Volumen- Verhältnis und struktureller Stabilität machen ihn zu einem wichtigen Baustein im Arsenal geometrischer Formen für das 21. Jahrhundert.