Abgeschrägtes Hexaeder berechnen

Rechner und Formeln zur Berechnung des abgeschrägten Hexaeders (Snub Cube)

Abgeschrägtes Hexaeder Rechner

Das abgeschrägte Hexaeder

Ein abgeschrägtes Hexaeder ist ein archimedischer Körper mit 38 Flächen: 6 Quadrate und 32 gleichseitige Dreiecke.

Bekannten Parameter eingeben

Parameter Type

Welcher Parameter ist bekannt?

Parameter Wert

Wert des ausgewählten Parameters

Dezimalstellen

Hexaeder-Eigenschaften

Kompakte Struktur: 24 Ecken, 60 Kanten, 38 Flächen

6 Quadrate 32 Dreiecke Archimedisch

Hexaeder-Berechnungsergebnisse

Seitenlänge a:

Volumen V:

Oberfläche S:

Umkugelradius r_c:

Kantenradius r_m:

Hexaeder-Struktur

Ein abgeschrägtes Hexaeder ist ein archimedischer Körper.
Es kombiniert Quadrate und gleichseitige Dreiecke.

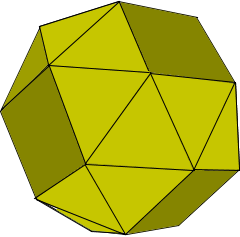
● 6 Quadrate ● 32 Dreiecke ● 24 Ecken

Was ist ein abgeschrägtes Hexaeder?

Ein abgeschrägtes Hexaeder (Snub Cube) ist einer der 13 archimedischen Körper:

38 Flächen: 6 Quadrate und 32 gleichseitige Dreiecke
24 Ecken: Jede Ecke wird von 4 Dreiecken und 1 Quadrat gebildet
60 Kanten: Alle Kanten haben die gleiche Länge

Chiralität: Existiert in zwei spiegelbildlichen Formen
Oktaedrische Symmetrie: Abgeleitet vom Würfel
Kompakte Form: Verhältnismäßig kleine Oberfläche

Geometrische Eigenschaften

Das abgeschrägte Hexaeder besitzt einzigartige geometrische Eigenschaften:

Flächenstruktur

6 Quadrate: Von den ursprünglichen Würfelflächen
32 Dreiecke: Durch die Abschrägungs-Operation entstanden
Einheitliche Kanten: Alle 60 Kanten sind gleich lang
Vertex-Figur: Jede Ecke: 4 Dreiecke + 1 Quadrat

Besondere Eigenschaften

Chiralität: Rechts- und linkshändige Formen
Oktaedrische Symmetrie: 24 Symmetrieoperationen
Tribische Konstante: Parameter t ≈ 1.839
Konvexer Körper: Alle Innenwinkel < 180°

Mathematische Beziehungen

Das abgeschrägte Hexaeder folgt präzisen mathematischen Gesetzen:

Volumenberechnung

V = a³ · Formel mit Parameter t

Das Volumen hängt von der tribischen Konstante t ab, die aus einer kubischen Gleichung stammt.

Oberflächenberechnung

S = 2a²(3 + 4√3)

Die Oberfläche kombiniert die Flächen von 6 Quadraten und 32 Dreiecken.

Anwendungen des abgeschrägten Hexaeders

Abgeschrägte Hexaeder finden sich in verschiedenen Bereichen:

Wissenschaft & Forschung

Kristallstrukturen und Materialwissenschaft
Molekulare Käfigstrukturen
Koordinationsgeometrie in der Chemie
Verpackungsprobleme und Optimierung

Kunst & Design

Skulpturen und geometrische Installationen
Schmuckdesign und Ornamentik
3D-Printing und Rapid Prototyping
Architektonische Designelemente

Spiele & Unterhaltung

Spezielle Würfel und Gaming-Zubehör
Puzzle und mechanische Spielzeuge
Virtual Reality Modellierung
Mathematische Lernspiele

Technik & Engineering

Robotik und mechanische Komponenten
Strukturelle Stabilitätselemente
Optische und photonische Komponenten
Biomedizinische Anwendungen

Formeln für das abgeschrägte Hexaeder

Konstante t

\[t=\frac{1+\sqrt[3]{19+3\sqrt{33}} +\sqrt[3]{19-3\sqrt{33}}}{3}\] \[t \approx 1.8392867552\]

Tribische Konstante aus kubischer Gleichung

Volumen V

\[V=\frac{a^3 \cdot (3\sqrt{t-1} +4\sqrt{t+1})}{3\sqrt{2-t}}\]

Komplexe Formel abhängig von Parameter t

Oberfläche S

\[S= 2a^2(3+4\sqrt{3})\]

Summe von 6 Quadraten und 32 Dreiecken

Umkugelradius r_c

\[r_c= a\sqrt{\frac{3-t}{4(2-t)}}\]

Radius der umschreibenden Kugel

Kantenradius r_m

\[r_m= a\sqrt{\frac{1}{4(2-t)}}\]

Radius der Kugel durch Kantenmittelpunkte

Seitenlänge a

\[a = \sqrt{\frac{S}{2(3+4\sqrt{3})}}\]

Aus anderen Parametern berechenbar

Rechenbeispiel für ein abgeschrägtes Hexaeder

Gegeben

Seitenlänge a = 10

Gesucht: Alle Eigenschaften des abgeschrägten Hexaeders

1. Konstante berechnen

\[t = 1.8392867552\] \[\sqrt{2-t} = 0.4009\]

Tribische Konstante und Hilfswerte

2. Oberflächenberechnung

\[S = 2 \times 100 \times (3 + 4\sqrt{3})\] \[S = 200 \times 9.928 = 1985.6\]

Oberfläche aus Seitenlänge

3. Volumenberechnung

\[V = \frac{1000 \times 6.889}{3 \times 0.4009}\] \[V = 5720.1\]

Komplexe Volumenformel anwenden

4. Radien berechnen

\[r_c = 10 \times 1.3437 = 13.44\] \[r_m = 10 \times 1.2468 = 12.47\]

Umkugel- und Kantenradius

5. Vollständiges abgeschrägtes Hexaeder

Seitenlänge a = 10.00 Oberfläche S = 1985.6

Volumen V = 5720.1 Umkugelradius = 13.44

Kantenradius = 12.47 38 Flächen total

Ein eleganter archimedischer Körper mit kompakter Struktur

Das abgeschrägte Hexaeder: Eleganz der kubischen Transformation

Das abgeschrägte Hexaeder (englisch: Snub Cube) ist einer der elegantesten archimedischen Körper und demonstriert auf faszinierende Weise, wie aus der simplen Würfelgeometrie durch eine einzige Transformation - die Abschrägung - ein hochkomplexer und ästhetisch ansprechender Polyeder entstehen kann. Mit seinen 38 Flächen verkörpert es die perfekte Balance zwischen geometrischer Komplexität und struktureller Harmonie.

Entstehung durch Abschrägung

Das abgeschrägte Hexaeder entsteht durch eine spezielle geometrische Operation am Würfel:

Ausgangsform: Regulärer Hexaeder (Würfel) mit 6 quadratischen Flächen
Abschrägungsoperation: Jede Ecke wird durch eine dreieckige Fläche ersetzt, wobei gleichzeitig eine Drehung erfolgt
Resultat: 6 ursprüngliche Quadrate bleiben erhalten, 32 neue gleichseitige Dreiecke entstehen
Kantenlänge: Alle 60 resultierenden Kanten haben identische Länge
Vertex-Konfiguration: Jede der 24 Ecken wird von 4 Dreiecken und 1 Quadrat gebildet (3.3.3.3.4)

Die tribische Konstante t

Der Schlüssel zur Berechnung des abgeschrägten Hexaeders ist die tribische Konstante:

Mathematische Herkunft

Die Konstante t ≈ 1.839287 ist die reelle Lösung einer kubischen Gleichung, die sich aus der Bedingung ergibt, dass alle Kanten gleich lang sein müssen. Diese Gleichung kann nicht durch einfache algebraische Operationen gelöst werden.

Geometrische Bedeutung

t beschreibt das Verhältnis zwischen den Kantenlängen des ursprünglichen Würfels und des resultierenden abgeschrägten Hexaeders. Es bestimmt den Grad der "Abschrägung" und damit alle anderen geometrischen Eigenschaften.

Numerische Berechnung

Die exakte Formel für t beinhaltet Kubikwurzeln komplexer Ausdrücke mit Quadratischen Wurzeln. Moderne Computerprogramme verwenden numerische Verfahren wie das Newton-Raphson-Verfahren für präzise Berechnungen.

Einzigartigkeit

Anders als beim goldenen Schnitt beim abgeschrägten Dodekaeder ist t eine algebraische Zahl dritten Grades. Diese Komplexität spiegelt sich in allen geometrischen Formeln wider.

Symmetrie und strukturelle Eigenschaften

Das abgeschrägte Hexaeder zeigt bemerkenswerte Symmetrieeigenschaften:

Oktaedrische Symmetriegruppe

Mit 24 Symmetrieoperationen gehört es zur oktaedrischen Symmetriegruppe O. Diese Symmetrie ist geringer als die ikosaedrische des abgeschrägten Dodekaeders, aber immer noch beachtlich komplex.

Chirale Formen

Wie sein größerer Verwandter existiert auch das abgeschrägte Hexaeder in zwei spiegelbildlichen Formen - einer rechts- und einer linkshändigen Version. Diese können nicht durch Rotation ineander überführt werden.

Duale Beziehungen

Das duale Polyeder zum abgeschrägten Hexaeder ist das Pentagonal Ikositetraeder, ein katalanischer Körper mit 24 unregelmäßigen fünfeckigen Flächen. Diese Dualität zeigt tiefere geometrische Verbindungen auf.

Kompaktheit

Verglichen mit anderen archimedischen Körpern gleicher Kantenlänge hat das abgeschrägte Hexaeder ein relativ großes Volumen bei relativ kleiner Oberfläche - ein Zeichen geometrischer Effizienz.

Anwendungen in Wissenschaft und Technik

Die praktischen Anwendungen des abgeschrägten Hexaeders sind vielfältig:

Kristallographie: Bestimmte Kristallstrukturen zeigen Annäherungen an diese Geometrie
Molekularchemie: Käfigmoleküle und Koordinationsverbindungen können diese Form aufweisen
Verpackungsindustrie: Optimale Raumausnutzung bei speziellen Anforderungen
Robotik: Gelenkstrukturen und mechanische Komponenten
Architektur: Raumstrukturen und innovative Bauformen
Spielindustrie: Speziell designte Würfel und Gaming-Komponenten
Optik: Facettierte Linsen und prismatische Strukturen

Konstruktion und Herstellung

Die praktische Umsetzung des abgeschrägten Hexaeders stellt interessante Herausforderungen dar:

Traditionelle Methoden

Die Konstruktion mit klassischen geometrischen Werkzeugen ist möglich, erfordert aber präzise numerische Approximationen von t. Holzarbeiter und Steinmetze entwickelten ingenieuse Näherungsverfahren.

Moderne Fertigung

3D-Druck und CNC-Fertigung ermöglichen heute präzise Umsetzungen. CAD-Software berechnet automatisch alle notwendigen Winkel und Dimensionen basierend auf der tribischen Konstante.

Materialherausforderungen

Die 38 verschiedenen Flächen erfordern präzise Winkel und Kanten. Besonders bei metallischen oder kristallinen Materialien sind exakte Toleranzen entscheidend für die strukturelle Integrität.

Qualitätskontrolle

Die Überprüfung der geometrischen Genauigkeit erfordert spezialisierte Messtechniken. Selbst kleine Abweichungen können die charakteristischen Eigenschaften des Polyeders beeinträchtigen.

Zusammenfassung

Das abgeschrägte Hexaeder verkörpert die elegante Transformation des einfachsten platonischen Körpers in eine komplexe, aber harmonische Form. Seine 38 Flächen, gesteuert durch die tribische Konstante t, demonstrieren wie mathematische Präzision und geometrische Schönheit Hand in Hand gehen. Als praktischer archimedischer Körper findet es Anwendungen von der Nanotechnologie bis zur Architektur, während seine chirale Natur zusätzliche Dimensionen der Komplexität eröffnet. In einer Zeit zunehmender digitaler Fertigung und präziser Materialbearbeitung wird das abgeschrägte Hexaeder zu einem wichtigen Baustein für innovative Designs und technologische Lösungen. Seine kompakte Form und effiziente Geometrie machen es zu einem zeitlosen Beispiel für die Kraft mathematischer Transformation und die Schönheit struktureller Eleganz.

Abgeschrägtes Dodekaeder • Abgeschrägtes Hexaeder • Dodekaederstumpf • Hexaederstumpf • Ikosidodekaeder • Ikosaederstumpf • Ikosidodekaederstumpf • Kuboktaeder • Kuboktaederstumpf • Oktaederstumpf • Rhombenikosidodekaeder • Rhombenkuboktaeder • Tetraederstumpf