Parallelogramm berechnen

Rechner und Formeln für das Rhomboid mit parallelen Seiten

Parallelogramm Rechner

Das Parallelogramm (Rhomboid)

Ein Parallelogramm hat zwei Paar paralleler Seiten mit gegenüberliegenden gleichen Winkeln.

Seitenlängen und Winkel eingeben
Erste parallele Seite
Zweite parallele Seite
Spitzer Winkel
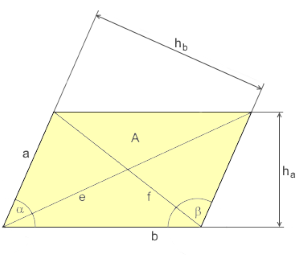
Parallelogramm Ergebnisse
Fläche A:
Umfang P:
Höhe ha:
Höhe hb:
Diagonale e:
Diagonale f:
Winkel β:

Parallelogramm Struktur

Parallelogramm Eigenschaften

Besonderheit: Gegenüberliegende Seiten parallel und gleich, α + β = 180°

a ∥ c, b ∥ d |a| = |c|, |b| = |d| α = γ, β = δ

Das Parallelogramm mit parallelen Seitenpaar a∥c und b∥d.
Gegenüberliegende Winkel sind gleich: α = γ, β = δ.

Parallelogramm


Das Parallelogramm: Eleganz der parallelen Linien

Das Parallelogramm (Rhomboid) ist ein fundamentales geometrisches Viereck:

  • Parallele Seiten: a ∥ c und b ∥ d (zwei Seitenpaare)
  • Gleiche Längen: |a| = |c| und |b| = |d|
  • Supplementwinkel: α + β = 180° (benachbarte Winkel)
  • Gleiche Gegenwinkel: α = γ und β = δ
  • Diagonalen halbieren sich: Schnittpunkt als Zentrum
  • Höhen-Beziehung: A = a · hb = b · ha

Geometrische Eigenschaften des Parallelogramms

Die besonderen Eigenschaften des Parallelogramms machen es vielseitig einsetzbar:

Parallelität und Symmetrie
  • Zwei Paar paralleler Seiten
  • Punktsymmetrisch zum Diagonalen-Schnittpunkt
  • Gegenüberliegende Seiten sind gleich lang
  • Keine Achsensymmetrie (außer bei Rechteck/Raute)
Winkel-Eigenschaften
  • Gegenüberliegende Winkel sind gleich
  • Benachbarte Winkel sind supplementär (180°)
  • Winkelsumme: α + β + γ + δ = 360°
  • Nur zwei verschiedene Winkelgrößen

Mathematische Berechnungen im Parallelogramm

Die Berechnungsmethoden für Parallelogramme sind vielfältig und elegant:

Flächen-Berechnung
  • A = a · hb = b · ha (Grundseite × Höhe)
  • A = a · b · sin(α) (Seiten × Sinus)
  • Höhen: ha = b · sin(α), hb = a · sin(α)
  • Drei äquivalente Berechnungsweisen
Diagonalen-Berechnung
  • Kosinussatz für beide Diagonalen
  • e = √(a² + b² - 2ab·cos(β))
  • f = √(a² + b² - 2ab·cos(α))
  • Diagonalen halbieren sich gegenseitig

Anwendungen des Parallelogramms

Parallelogramme finden vielfältige praktische Anwendungen:

Architektur & Bauwesen
  • Dachkonstruktionen mit Parallelogramm-Form
  • Fachwerk-Strukturen und Verstrebungen
  • Fenster- und Türrahmen (schiefe Öffnungen)
  • Moderne Gebäude-Geometrie
Technik & Maschinenbau
  • Getriebe und Übertragungsmechanismen
  • Parallelogramm-Lenker in der Mechanik
  • Pantograph-Systeme (Stromabnehmer)
  • Scheibenwischer-Mechanismen
Design & Kunst
  • Grafik-Design und Layout-Gestaltung
  • Typografie (kursive Schriften)
  • Logo-Design mit dynamischen Formen
  • Architektur-Visualisierung
Physik & Mathematik
  • Kräfteparallelogramm in der Mechanik
  • Vektoraddition und Zerlegung
  • Koordinaten-Transformationen
  • Kristallographie (Gitterstrukturen)

Formeln für das Parallelogramm

Flächeninhalt A
\[A = b \cdot h_a = a \cdot h_b = a \cdot b \cdot \sin(\alpha)\]

Drei äquivalente Berechnungsmethoden

Umfang P
\[P = 2 \cdot (a + b)\]

Doppelte Summe der benachbarten Seiten

Höhen ha und hb
\[h_a = \frac{A}{b} = a \cdot \sin(\alpha)\] \[h_b = \frac{A}{a} = b \cdot \sin(\alpha)\]

Höhen aus Flächeninhalt oder Trigonometrie

Diagonalen e und f
\[e = \sqrt{a^2 + b^2 - 2ab \cos(\beta)}\] \[f = \sqrt{a^2 + b^2 - 2ab \cos(\alpha)}\]

Kosinussatz für beide Diagonalen

Seitenlängen aus Flächeninhalt
\[a = \frac{A}{h_b} = \frac{A}{b \cdot \sin(\alpha)}\] \[b = \frac{A}{h_a} = \frac{A}{a \cdot \sin(\alpha)}\]

Rückwärts-Berechnung der Seiten

Winkel α aus Flächeninhalt
\[\alpha = \arcsin\left(\frac{A}{a \cdot b}\right)\]

Winkel aus gegebener Fläche berechnen

Winkel-Beziehungen
\[\alpha + \beta = 180° \quad\text{und}\quad \alpha = \gamma, \beta = \delta\]

Supplementäre benachbarte Winkel, gleiche gegenüberliegende Winkel

Rechenbeispiel für ein Parallelogramm

Gegeben
Seite a = 5 Seite b = 3 Winkel α = 60°

Gesucht: Alle Parameter des Parallelogramms

1. Fläche und Umfang
\[A = 5 \times 3 \times \sin(60°) = 15 \times 0.866 = 12.99\] \[P = 2 \times (5 + 3) = 16\]

Fläche mit Sinus-Formel, Umfang als Seitensumme

2. Höhen berechnen
\[h_a = 3 \times \sin(60°) = 3 \times 0.866 = 2.60\] \[h_b = 5 \times \sin(60°) = 5 \times 0.866 = 4.33\]

Höhen durch trigonometrische Beziehung

3. Winkel und Diagonalen
β = 180° - 60° = 120° e = √(25 + 9 - 2×5×3×cos(120°)) = 7.00
f = √(25 + 9 - 2×5×3×cos(60°)) = 4.36 γ = α = 60°, δ = β = 120°

Supplementwinkel β und Diagonalen mit Kosinussatz

4. Vollständiges Parallelogramm
Seiten: a=5, b=3, c=5, d=3 Winkel: α=60°, β=120°, γ=60°, δ=120°
Umfang P = 16 Fläche A = 12.99 Höhen: ha=2.60, hb=4.33 Diagonalen: e=7.00, f=4.36

Das komplette Parallelogramm - elegante Parallelität in der Praxis!

Das Parallelogramm: Eleganz der Parallelität in Geometrie und Technik

Das Parallelogramm steht als fundamentale geometrische Form für das Prinzip der Parallelität. Mit zwei Paaren paralleler Seiten und der charakteristischen Eigenschaft, dass sich gegenüberliegende Seiten und Winkel gleichen, verkörpert es geometrische Harmonie und findet vielfältige Anwendungen von der Mechanik bis zur modernen Architektur.

Die Schönheit der parallelen Geometrie

Das Parallelogramm fasziniert durch seine eleganten Eigenschaften:

  • Doppelte Parallelität: Zwei Seitenpaare a∥c und b∥d schaffen stabile Struktur
  • Symmetrie der Gegensätze: Gegenüberliegende Seiten und Winkel sind gleich
  • Supplementäre Harmonie: Benachbarte Winkel ergänzen sich zu 180°
  • Zentrale Symmetrie: Punktsymmetrisch bezüglich des Diagonalen-Schnittpunkts
  • Dreifache Flächenformel: A = a·hb = b·ha = a·b·sin(α)
  • Diagonalen-Halbierung: Beide Diagonalen halbieren sich gegenseitig

Parallelogramme in der Natur und Technik

Die Natur und menschliche Technik nutzen Parallelogramm-Strukturen für Stabilität und Funktion:

Mechanische Systeme

Parallelogramm-Lenker in der Fahrzeugtechnik sorgen für gleichmäßige Bewegungen. Pantographen bei Zügen nutzen diese Geometrie für konstanten Kontakt zur Oberleitung.

Kristallstrukturen

Viele Minerale bilden parallelogrammartige Gitterstrukturen. Diese Anordnung minimiert Energie und maximiert strukturelle Stabilität.

Architektur und Konstruktion

Moderne Architektur nutzt Parallelogramm-Formen für dynamische Gebäude-Silhouetten. Fachwerk-Konstruktionen verwenden diese Geometrie für optimale Lastverteilung.

Physik und Kräfte

Das Kräfteparallelogramm ist fundamental in der Mechanik. Vektoraddition und Kräftezerlegung basieren auf parallelogrammatischen Prinzipien.

Mathematische Eleganz und Berechnungsvielfalt

Das Parallelogramm bietet bemerkenswerte mathematische Flexibilität:

  • Drei Flächenformeln: Grundseite×Höhe, Seiten×Sinus, Höhe-abhängige Varianten
  • Trigonometrische Beziehungen: Höhen als ha = b·sin(α), hb = a·sin(α)
  • Kosinussatz für Diagonalen: Beide Diagonalen durch eine einheitliche Formel
  • Winkel-Arithmetik: α + β = 180°, nur zwei unabhängige Winkel
  • Umkehrbarkeit: Alle Parameter aus verschiedenen Ausgangswerten berechenbar
  • Spezialfälle: Rechteck (α = 90°) und Raute (a = b) als Sonderformen

Moderne Anwendungen und Zukunftsperspektiven

Das Parallelogramm gewinnt in der digitalen Ära neue Bedeutung:

Computer Graphics

Parallelogramme sind Grundbausteine für Texture-Mapping und 3D-Transformationen. Affine Transformationen erhalten Parallelität.

Robotik und Automation

Parallelogramm-Mechanismen in Industrierobotern sorgen für präzise, wiederholbare Bewegungen. Delta-Roboter nutzen diese Geometrie für Hochgeschwindigkeits-Operationen.

Architektur-Innovation

Parametrische Architektur nutzt Parallelogramm-Variationen für adaptive Fassaden. Smart Buildings verwenden diese Geometrie für bewegliche Verschattungssysteme.

Material Science

Metamaterialien mit parallelogrammatischen Strukturen zeigen besondere mechanische Eigenschaften. Negative Poisson-Ratios entstehen durch clevere Parallelogramm-Anordnungen.

Parallelogramme als Design-Prinzip

Das Parallelogramm inspiriert modernes Design durch seine dynamische Statik:

  • Visuelle Dynamik: Schiefe Winkel erzeugen Bewegungsillusion bei statischen Objekten
  • Typografisches Design: Kursive Schriften basieren auf Parallelogramm-Prinzipien
  • Logo-Design: Parallelogramme vermitteln Fortschritt und Dynamik
  • UI/UX-Design: Schiefe Interface-Elemente schaffen moderne Ästhetik
  • Industriedesign: Parallelogramm-Formen suggerieren Geschwindigkeit und Effizienz
  • Architektonische Identität: Parallelogramm-Gebäude werden zu markanten Landmarks
Zusammenfassung

Das Parallelogramm verkörpert die perfekte Balance zwischen geometrischer Stabilität und visueller Dynamik. Seine charakteristischen parallelen Seitenpaare schaffen eine Grundstruktur, die sowohl in der Natur als auch in der menschlichen Technik unverzichtbar ist. Von mechanischen Systemen über architektonische Meisterwerke bis hin zu modernen digitalen Interfaces - das Parallelogramm beweist seine Vielseitigkeit durch mathematische Eleganz und praktische Funktionalität. In einer Welt, die zunehmend auf Effizienz, Stabilität und ästhetische Innovation setzt, bleibt das Parallelogramm ein zeitloses Werkzeug für Designer, Ingenieure und Architekten. Es erinnert uns daran, dass wahre Schönheit oft in der Einfachheit liegt - zwei parallele Linienpaare, die unendliche Möglichkeiten eröffnen.

Weitere Viereck Funktionen

Quadrat • Rechteck • Goldenes Rechteck • Rechteck und Quadrat • Parallelogramm • Parallelogramm Flächeninhalt • Raute • Raute Flächeninhalt • Allgemeines Viereck • Sehnenviereck • Konkaves Viereck • Pfeilviereck • Überschlagenes Viereck • Rahmen • Drachenviereck • Drachenviereck Flächeninhalt • Drachenviereck, Halbquadrat • Drachenviereck, rechtwinklig