Rechteck berechnen
Rechner und Formeln für das klassische Rechteck
Rechteck Rechner
Das Rechteck
Ein Rechteck hat vier rechte Winkel und parallel gegenüberliegende Seiten.
Rechteck Struktur
Rechteck Eigenschaften
Grundform: Vier rechte Winkel, gegenüberliegende Seiten gleich
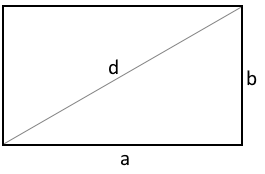
Rechteck mit Länge a und Breite b.
Alle Innenwinkel betragen 90°.
|
|
Das Rechteck: Fundament der rechtwinkligen Geometrie
Das Rechteck ist die fundamentale Form der rechtwinkligen Geometrie:
- Vier rechte Winkel: Jeder Innenwinkel = 90°
- Parallele Seiten: Gegenüberliegende Seiten parallel
- Gleiche Gegenseiten: a₁ = a₂ und b₁ = b₂
- Gleiche Diagonalen: Beide Diagonalen haben Länge d
- Diagonalen-Halbierung: Diagonalen halbieren sich
- Umkreis-Existenz: Mittelpunkt = Diagonalen-Schnittpunkt
Geometrische Eigenschaften des Rechtecks
Die mathematischen Eigenschaften des Rechtecks sind klar definiert:
Winkel-Eigenschaften
- Alle vier Innenwinkel sind rechte Winkel (90°)
- Winkelsumme: 4 × 90° = 360°
- Keine spitzen oder stumpfen Winkel
- Perfekte Orthogonalität aller Seitentreffen
Seiten-Beziehungen
- Gegenüberliegende Seiten gleich lang
- Gegenüberliegende Seiten parallel
- Benachbarte Seiten senkrecht zueinander
- Zwei verschiedene Seitenlängen (a ≠ b meist)
Mathematik der Rechteck-Berechnung
Die mathematischen Beziehungen des Rechtecks sind elementar:
Flächen-Berechnung
- Fläche: A = a × b (Länge mal Breite)
- Einfachste Flächenformel aller Vierecke
- Basis für komplexere Flächenberechnungen
- Direkte Multiplikation ohne Trigonometrie
Pythagorische Beziehung
- Diagonale: d = √(a² + b²)
- Pythagorischer Satz anwendbar
- Rechtwinklige Dreiecke in den Ecken
- Diagonale als Hypotenuse
Anwendungen des Rechtecks
Rechtecke sind omnipräsent in unserer strukturierten Welt:
Architektur & Bauwesen
- Grundrisse und Raumplanung
- Fenster, Türen und Öffnungen
- Fassaden-Gestaltung
- Strukturelle Rahmen-Systeme
Digitale Welt
- Bildschirme und Displays
- Webseiten-Layout und UI-Design
- Pixel-Arrays und Raster-Systeme
- Fenster und Dialog-Boxen
Produktion & Fertigung
- Materialzuschnitt und -planung
- Verpackungs-Design
- Maschinenbau-Komponenten
- Elektronik-Platinen und Gehäuse
Kunst & Design
- Leinwände und Bilderrahmen
- Typografie und Layout-Design
- Möbel-Design und Innenarchitektur
- Grafische Raster-Systeme
Formeln für das Rechteck
Länge a
Länge aus Fläche und Breite
Breite b
Breite aus Fläche und Länge
Flächeninhalt A
Länge mal Breite - einfachste Flächenformel
Umfang P
Doppelte Summe beider Seitenlängen
Diagonale d
Pythagorischer Satz - Diagonale als Hypotenuse
Rechenbeispiel für ein Rechteck
Gegeben
Gesucht: Alle Parameter des Rechtecks
1. Fläche berechnen
Einfache Multiplikation der Seiten
2. Umfang berechnen
Summe aller vier Seitenlängen
3. Diagonale mit Pythagoras
Pythagorischer Satz für rechtwinklige Dreiecke
4. Vollständiges Rechteck
Das klassische 3-4-5 Rechteck - ein pythagorisches Tripel!
Das Rechteck: Grundstein der rechtwinkligen Geometrie
Das Rechteck steht als fundamentale Form der Geometrie im Zentrum menschlicher Kultur und Technik. Mit seinen vier rechten Winkeln und parallelen Gegenseiten verkörpert es Ordnung, Struktur und mathematische Klarheit. Von antiken Tempeln über moderne Bildschirme bis hin zu digitalen Interfaces - das Rechteck prägt unsere visuelle und strukturelle Welt durch seine perfekte Balance zwischen Einfachheit und funktionaler Vielseitigkeit.
Die mathematische Reinheit des Rechtecks
Das Rechteck verkörpert mathematische Grundprinzipien in reinster Form:
- Rechtwinkligkeit: Vier perfekte 90°-Winkel ohne Ausnahme
- Parallelität: Gegenüberliegende Seiten exakt parallel
- Gleichheit der Gegenseiten: a₁ = a₂ und b₁ = b₂
- Pythagorische Diagonale: d = √(a² + b²) - fundamentaler Bezug
- Einfachste Flächenformel: A = a × b - keine Trigonometrie erforderlich
- Umkreis-Existenz: Eindeutig bestimmter Umkreis mit Mittelpunkt
Das Rechteck in der Kulturgeschichte
Kulturell hat das Rechteck eine tiefe historische Bedeutung:
Antike Architektur
Griechische Tempel und römische Basiliken nutzten rechteckige Grundrisse für Stabilität und Harmonie. Der Goldene Schnitt in rechteckigen Proportionen wurde zur ästhetischen Norm.
Mittelalterliche Stadtplanung
Römische Castra und mittelalterliche Stadtgründungen folgten rechteckigen Rastern. Diese Ordnung erleichterte Verwaltung und Verteidigung.
Renaissance und Moderne
Perspektive und Fluchtpunkt-Konstruktionen basierten auf rechteckigen Koordinatensystemen. Bauhaus-Design erhob das Rechteck zum Gestaltungsprinzip.
Digitale Revolution
Pixel, Bildschirme und User Interfaces sind grundlegend rechteckig strukturiert. Die digitale Welt ist eine Welt der Rechtecke.
Technische Omnipräsenz des Rechtecks
In der modernen Technik ist das Rechteck allgegenwärtig:
- Display-Technologie: Bildschirme, Smartphones, Tablets - alle rechteckig
- Architektonische Systeme: Modulbauweise und Raster-Konstruktionen
- Elektronik-Design: Platinen, Chips und Gehäuse folgen rechteckigen Normen
- Software-Interfaces: Fenster, Buttons und Layout-Systeme
- Produktionseffizienz: Rechteckiger Zuschnitt minimiert Materialverschwendung
- Logistik-Optimierung: Container und Verpackungen für maximale Raumausnutzung
Psychologie und Wahrnehmung rechteckiger Formen
Die Wirkung des Rechtecks auf menschliche Wahrnehmung ist tiefgreifend:
Kognitive Verarbeitung
Das menschliche Gehirn verarbeitet rechteckige Strukturen besonders effizient. Rechtecke werden schneller erkannt und kategorisiert als andere Formen.
Ordnungs-Psychologie
Rechteckige Anordnungen vermitteln Ordnung, Stabilität und Vertrauen. Sie reduzieren kognitive Belastung und fördern Übersichtlichkeit.
Kulturelle Prägung
Westliche Kulturen assoziieren Rechtecke mit Rationalität und Fortschritt. Sie symbolisieren technischen und gesellschaftlichen Entwicklungsstand.
Design-Prinzipien
Rechteckige Grids ermöglichen harmonische Proportionen und ästhetische Balance. Sie sind Grundlage moderner Typografie und Layout-Gestaltung.
Zukunftsperspektiven der Rechteck-Geometrie
Die Zukunft bringt neue Anwendungen für rechteckige Strukturen:
- Flexible Displays: Faltbare und biegbare rechteckige Bildschirme
- Smart Buildings: Adaptive rechteckige Module für wandelbare Architektur
- Nano-Strukturierung: Rechteckige Arrays auf molekularer Ebene
- Quantum Computing: Rechteckige Qubit-Anordnungen für Stabilität
- Augmented Reality: Rechteckige Overlays für räumliche Information
- Sustainable Design: Modulare rechteckige Systeme für Kreislaufwirtschaft
Zusammenfassung
Das Rechteck steht als zeitloses Symbol für Ordnung, Klarheit und funktionale Perfektion. Seine vier rechten Winkel und parallelen Seiten verkörpern die Essenz strukturierten Denkens und rationaler Gestaltung. Von der antiken Architektur über die digitale Revolution bis hin zu zukünftigen Technologien bleibt das Rechteck der fundamentale Baustein unserer visuellen und technischen Welt. Es erinnert uns daran, dass in der scheinbaren Einfachheit - vier Linien, vier Winkel - unendliche Möglichkeiten liegen. Das Rechteck ist nicht nur eine geometrische Form, sondern ein kulturelles Paradigma, das Ordnung schafft, Effizienz ermöglicht und ästhetische Harmonie stiftet.
|
|
|
|