Matrix Addition 3×3
Onlinerechner zum Addieren von 3x3 Matrizen
Matrix Addition Rechner
Anleitung
Geben Sie die Werte beider Matrizen ein, die addiert werden sollen. Leere Felder werden als Null gewertet. Klicken Sie dann auf Rechnen.
Matrix Addition - Übersicht
Grundregel
Zur Matrizen-Addition müssen die Matrizen übereinstimmen.
Sie müssen die gleiche Anzahl von Zeilen und Spalten haben.
Addition
Um eine Matrizenaddition auszuführen, werden die entsprechenden Matrizenelemente addiert:
C[i,j] = A[i,j] + B[i,j]
Beispiel
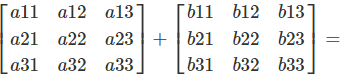
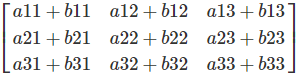
Eigenschaften
- Kommutativ: A + B = B + A
- Assoziativ: (A + B) + C = A + (B + C)
- Null-Element: A + 0 = A
- Inverses: A + (-A) = 0
|
|
Detaillierte Beschreibung zur Matrizen Addition
Matrix Addition
Zur Matrizen-Addition oder Subtraktion müssen die Matrizen übereinstimmen. Das heißt, sie müssen die gleiche Anzahl von Zeilen und die gleiche Anzahl von Spalten haben.
Um eine Matrizenaddition auszuführen, werden die entsprechenden Matrizenelemente addiert. Jedes Element der Ergebnismatrix ist die Summe der Elemente an derselben Position in den beiden Ausgangsmatrizen.
Für Matrizen A und B gilt:
C = A + Bwobei jedes Element:
cij = aij + bij
Voraussetzungen
- Beide Matrizen müssen die gleiche Dimension haben
- Für 3×3 Matrizen: Beide müssen 3 Zeilen und 3 Spalten haben
- Die Addition ist nur für Matrizen gleicher Größe definiert
Berechnungsbeispiel
Gegeben:
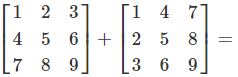
Berechnung:
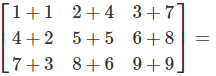
Ergebnis:

Rechenregeln
- Kommutativgesetz: A + B = B + A
- Assoziativgesetz: (A + B) + C = A + (B + C)
- Distributivgesetz: k(A + B) = kA + kB
- Neutrales Element: A + 0 = A
- Inverses Element: A + (-A) = 0
Praktische Anwendungen
Mathematik & Physik:
- Vektoraddition in mehreren Dimensionen
- Transformation von Koordinatensystemen
- Lösung linearer Gleichungssysteme
Informatik & Technik:
- Bildverarbeitung (Pixel-Operationen)
- Computergrafik (3D-Transformationen)
- Datenanalyse und Statistik
|
|