Matrix Subtraction 3×3

Online calculator for subtracting 3x3 matrices

Matrix Subtraction Calculator

Instructions

Enter the values of both matrices to be subtracted. Empty fields are counted as zero. Click Calculate.

Matrix A
| |
| |
| |
−
Matrix B
| |
| |
| |
Result: A − B
| |
| |
| |

Matrix Subtraction - Overview

Prerequisites

For matrix subtraction, the matrices must match. That is, they must have the same number of rows and columns. Both matrices must be 3×3.

Calculation Formula

For a matrix subtraction, the individual elements of the matrices are subtracted from each other:

\(C_{ij} = A_{ij} - B_{ij}\)

Example

Given:

\(\displaystyle A = \begin{bmatrix}1 & 2 & 3\\4 & 5 & 6\\7 & 8 & 9\end{bmatrix}, \quad B = \begin{bmatrix}1 & 4 & 7\\2 & 5 & 8\\3 & 6 & 9\end{bmatrix}\)

Result:

\(A - B = \begin{bmatrix}0 & -2 & -4\\2 & 0 & -2\\4 & 2 & 0\end{bmatrix}\)

Properties
  • Not commutative: A − B ≠ B − A (order matters!)
  • Associative: (A − B) − C = A − (B + C)
  • Identity: A − 0 = A
  • Inverse: A − A = 0 (zero matrix)
  • Distributive: k(A − B) = kA − kB
  • Same dimensions: Result has same size as inputs


Description of Matrix Subtraction

Fundamentals

For matrix subtraction, the matrices must match. That is, they must have the same number of rows and columns. This is one of the basic operations in matrix algebra.

General Formula:

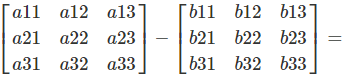
Matrix subtraction formula 1

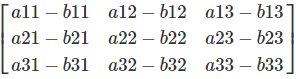
Matrix subtraction formula 2

How It Works

For a matrix subtraction, the individual elements of the matrices are subtracted from each other. Each element in position (i,j) of matrix A is subtracted by the corresponding element at position (i,j) in matrix B.

  1. Check dimensions: Both matrices must be 3×3
  2. Subtract each element: Cij = Aij − Bij
  3. The result is a new matrix with the same dimensions

Detailed Example

Step-by-Step Calculation

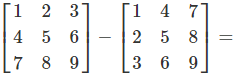
Matrix subtraction example 1

Matrix subtraction example 2

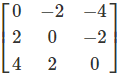
Matrix subtraction example 3

Important Properties
  • Not commutative: A − B ≠ B − A (different result!)
  • Associative: (A − B) − C = A − (B + C)
  • Identity element: A − 0 = A (zero matrix)
  • Self-subtraction: A − A = 0 (zero matrix)
  • Scalar multiplication: k(A − B) = kA − kB
  • Relation to addition: A − B = A + (−B)
Practical Applications

Mathematics & Physics:

  • Computing differences between states
  • Finding error matrices (actual − expected)
  • Comparing transformation matrices
  • Solving systems of equations

Engineering & Computer Science:

  • Image processing (difference images)
  • Machine learning (gradient computation)
  • Computer graphics (relative transformations)
  • Data analysis (change detection)
Important Note

Matrix subtraction is NOT commutative! This means A − B ≠ B − A. In fact, B − A = −(A − B). The order of subtraction matters. For example, if A = [1 2; 3 4] and B = [5 6; 7 8], then A − B = [−4 −4; −4 −4] but B − A = [4 4; 4 4] - completely opposite results!