Matrix X-Axis Rotation 4×4
Calculator for rotating around the X-axis
X-Axis Rotation Calculator
Instructions
Enter the rotation angle for rotation around the X-axis. Choose between active (rotate object) or passive (rotate coordinates) rotation.
X-Axis Rotation - Overview
What is X-Axis Rotation?
X-axis rotation rotates points around the X-axis (horizontal axis). The Y and Z coordinates change while X remains constant.
Active Rotation Formula
Counterclockwise rotation (right-hand rule):
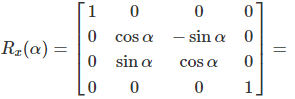
Example: 90° Rotation
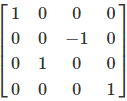
Key Properties
- X-coordinate: Remains unchanged
- Y and Z: Rotate in YZ-plane
- Active rotation: Counterclockwise (geometric transformation)
- Passive rotation: Clockwise (coordinate system rotation)
- Orthogonal matrix: RT = R-1
|
|
Description of X-Axis Rotation
Fundamentals
The matrix rotation distinguishes between active and passive rotation. Both are important in different contexts of 3D graphics and engineering.
Active Rotation
With active rotation, the vector or the object is rotated in the coordinate system. The active rotation is also called a geometric transformation. The rotation is counterclockwise.
Example of a 90° rotation around the X-axis:
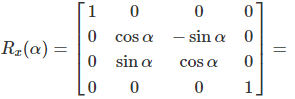
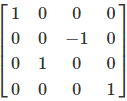
Matrix Structure
The X-axis rotation matrix has a special structure:
- First row/column: [1, 0, 0, 0] - X unchanged
- 3×3 submatrix: 2D rotation in YZ-plane
- Last row/column: [0, 0, 0, 1] - Homogeneous coordinate
- Determinant: det(R) = 1 (preserves volume)
Passive Rotation
With passive rotation, the coordinate system is rotated. The vector remains unchanged. The rotation is clockwise.
Example of a 90° rotation around the X-axis:
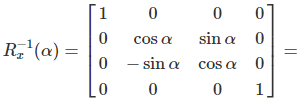
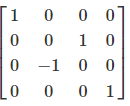
Relationship
Active vs Passive
The passive rotation matrix is the inverse (transpose) of the active rotation matrix:
\(R_x^{passive}(\theta) = R_x^{active}(-\theta) = R_x^{active}(\theta)^T\)
Practical Applications
3D Graphics & Gaming:
- Roll rotation: Aircraft roll around longitudinal axis
- Character animation: Torso rotation
- Camera roll: Tilting the camera
- Wheel rotation: Car wheels spinning
Engineering & Robotics:
- Joint rotation: Robot arm joints around X-axis
- Coordinate transforms: Between different reference frames
- Gimbal systems: First axis of rotation
- CAD modeling: Part rotation for viewing
Right-Hand Rule for X-Axis
Active Rotation (Counterclockwise):
- Point your right thumb along the positive X-axis (to the right)
- Curl your fingers naturally
- Your fingers curl from +Y toward +Z
- This is the positive rotation direction
Effect on Coordinates:
- X-coordinate: Always unchanged
- +Y axis (0,1,0): Rotates toward +Z
- +Z axis (0,0,1): Rotates toward -Y
- 90° rotation: Y→Z, Z→-Y
Mathematical Properties
Rotation Matrix Properties:
- Orthogonal: RTR = I
- Inverse: R-1 = RT
- Determinant: det(R) = 1
- Preserves length: ||Rv|| = ||v||
- Preserves angles: (Rv)·(Rw) = v·w
Combination Rules:
- Sequential rotations: Rx(θ₂)Rx(θ₁) = Rx(θ₁+θ₂)
- Commutative: Rx(θ₁)Rx(θ₂) = Rx(θ₂)Rx(θ₁)
- Identity: Rx(0) = I
- Full rotation: Rx(360°) = I
Important Notes
- X-axis rotations commute: Multiple X-axis rotations can be combined by simply adding the angles: Rx(30°)·Rx(45°) = Rx(75°)
- NOT commutative with other axes: Rx·Ry ≠ Ry·Rx. The order of rotations around different axes matters!
- Active vs Passive: Choose the correct mode for your application. 3D graphics typically use active rotation, while coordinate transformations often use passive.
- Gimbal lock: When using Euler angles (X, Y, Z rotations), certain angle combinations can cause gimbal lock. Consider using quaternions for complex rotations.
X-Rotation in Euler Angles
The X-axis rotation is typically one component of Euler angles (often called Roll-Pitch-Yaw):
Roll (X-axis):
- Bank angle
- Tilt left/right
- Aircraft wings up/down
Pitch (Y-axis):
- Nose up/down
- Looking up/down
- Aircraft climb/descend
Yaw (Z-axis):
- Turn left/right
- Compass heading
- Aircraft turn
Combined rotation: R = Rz(yaw) · Ry(pitch) · Rx(roll) (order matters!)
|
|