Pentagonikositetraeder Rechner

Rechner und Formeln zur Berechnung eines Pentagonikositetraeder

Der Pentagon-Körper - 24 Fünfecksflächen in Tribonacci-Harmonie!

Pentagonikositetraeder Rechner

Das Pentagonikositetraeder

Ein Pentagonikositetraeder ist ein katalanischer Körper mit 24 unregelmäßigen Fünfecksflächen - dual zum abgeschrägten Hexaeder.

Bekannten Parameter eingeben
Welcher Parameter ist bekannt?
Wert des ausgewählten Parameters
Pentagonikositetraeder Berechnungsergebnisse
Lange Kante a:
Kurze Kante b:
Oberfläche A:
Volumen V:
Kantenradius RK:
Innenradius RI:
Pentagonikositetraeder Eigenschaften

Der Pentagon-Körper: Dual zum abgeschrägten Hexaeder

24 Fünfecksflächen 60 Kanten 38 Ecken Tribonacci-Konstante

Pentagonikositetraeder Struktur

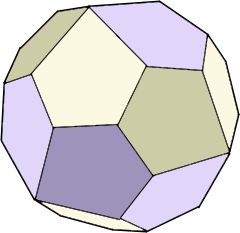
Pentagonikositetraeder

Der Pentagon-Körper mit 24 Fünfecksflächen.
Dual zum abgeschrägten Hexaeder.


Was ist ein Pentagonikositetraeder?

Ein Pentagonikositetraeder ist ein einzigartiger katalanischer Körper mit Fünfecksflächen:

  • Definition: Polyeder mit 24 unregelmäßigen Fünfecksflächen
  • Flächen: Jede Fläche ist ein unregelmäßiges Pentagon
  • Dual: Zum abgeschrägten Hexaeder (38 Flächen)
  • Ecken: 38 verschiedene Eckentypen
  • Kanten: 60 Kanten in zwei Längen
  • Mathematik: Tribonacci-Konstante bestimmt Proportionen

Geometrische Eigenschaften des Pentagonikositetraeders

Das Pentagonikositetraeder zeigt bemerkenswerte pentagonale Eigenschaften:

Pentagon-Parameter
  • Kantenlängen: Zwei verschiedene Kantenlängen a und b
  • Flächen: 24 kongruente unregelmäßige Fünfecke
  • Euler-Charakteristik: V - E + F = 38 - 60 + 24 = 2
  • Dualform: Abgeschrägtes Hexaeder
Pentagonale Eigenschaften
  • Katalanischer Körper: Dual zu uniformem Polyeder
  • Fünfecksflächen: Jede Fläche ist ein unregelmäßiges Pentagon
  • Tribonacci-Konstante: t ≈ 1.839 bestimmt Proportionen
  • Kubische Symmetrie: Vom dualen Hexaeder abgeleitet

Mathematische Beziehungen

Das Pentagonikositetraeder folgt einzigartigen mathematischen Gesetzen der Tribonacci-Konstante:

Tribonacci-Volumen
V ≈ 2.18·a³

Komplexe Formel mit Tribonacci-Konstante t. Parameter s = (t-1)/2 ≈ 0.42 bestimmt Geometrie.

Pentagon-Oberfläche
A ≈ 7.66·a²

Summe von 24 unregelmäßigen Fünfecken. Tribonacci-Konstante in pentagonaler Form.

Anwendungen des Pentagonikositetraeders

Pentagonikositetraeder finden Anwendung in pentagonalen Strukturen:

Wissenschaft & Forschung
  • Pentagonale Kristallstrukturen und Quasikristalle
  • Tribonacci-Sequenz Anwendungen
  • Mathematische Fünfeck-Tessellationen
  • Pentagonale Symmetriestudien
Technik & Design
  • 3D-Modellierung pentagonaler Formen
  • Algorithmus-Tests für Fünfeck-Geometrien
  • Architektonische Pentagon-Elemente
  • Tribonacci-basierte Berechnungen
Bildung & Lehre
  • Pentagonale Geometrie Demonstrationen
  • Tribonacci-Konstante Studien
  • Katalanische Körper mit Fünfecken
  • Dualitäts-Prinzipien bei Pentagonen
Kunst & Gestaltung
  • Pentagonale Skulpturen und Installationen
  • Fünfeck-basierte Muster und Ornamente
  • Tribonacci-inspirierte Designs
  • Architektonische Pentagon-Motive

Formeln für das Pentagonikositetraeder

Tribonacci-Konstante t und Parameter s
\[t ≈ 1.839286755214161\] \[s = \frac{t-1}{2} ≈ 0.41964337760708\]

Fundamentale Konstante für alle pentagonalen Berechnungen

Oberfläche A
\[A = \frac{24a^2(2+3s)\sqrt{\frac{1-s}{1+s}}}{1+2s}\] \[A ≈ 7.66 \cdot a^2\]

Oberfläche mit Tribonacci-Parameter s

Volumen V
\[V = \frac{4a^3(2+3s)\sqrt{1-2s}}{(1+s)(1-4s^2)}\] \[V ≈ 2.18 \cdot a^3\]

Volumen mit komplexen Tribonacci-Beziehungen

Kantenradius RK
\[R_K = \frac{a}{\sqrt{2(1+s)(1-2s)}}\] \[R_K ≈ 0.91 \cdot a\]

Kantenradius mit Tribonacci-Parameter

Innenradius RI
\[R_I = \frac{a}{2\sqrt{(1-2s)(1-s^2)}}\] \[R_I ≈ 0.77 \cdot a\]

Innenradius mit Tribonacci-Abhängigkeit

Pentagon-Eigenschaften (Tribonacci-Version)
Lange Kante a
Grundparameter
Kurze Kante b
b = a/(s+1) ≈ 0.71a

Jedes der 24 unregelmäßigen Fünfecke hat Tribonacci-Proportionen

Tribonacci-Kantenverhältnisse
Kanten-Verhältnis
a/b = s+1 ≈ 1.42
Tribonacci-Beziehung
Parameter s bestimmt alle Proportionen

Charakteristische Tribonacci-Beziehungen der pentagonalen Struktur

Berechnungsbeispiel für ein Pentagonikositetraeder

Gegeben
Lange Kante a = 6

Gesucht: Alle Eigenschaften des Pentagon-Körpers

1. Oberflächenberechnung
\[A = 7.66 \times 6^2\] \[A = 7.66 \times 36\] \[A = 275.8\]

Die Oberfläche beträgt etwa 276 Flächeneinheiten

2. Volumenberechnung
\[V = 2.18 \times 6^3\] \[V = 2.18 \times 216\] \[V = 470.9\]

Das Volumen beträgt etwa 471 Kubikeinheiten

3. Kurze Kante
\[b = \frac{6}{s+1} = \frac{6}{1.42}\] \[b = 4.23\]

Die kurze Kante beträgt etwa 4.23 Einheiten

4. Radien
\[R_K = 0.91 \times 6 = 5.46\] \[R_I = 0.77 \times 6 = 4.62\]

Kantenradius: 5.46, Innenradius: 4.62 Einheiten

5. Der Pentagon-Körper
Lange Kante a = 6.00 Kurze Kante b = 4.23 Oberfläche A = 275.8
Volumen V = 470.9 Kantenradius RK = 5.46 Innenradius RI = 4.62
24 Fünfecksflächen ⭐ Tribonacci-Harmonie Pentagon-Geometrie

Der einzigartige Pentagon-Körper mit Tribonacci-Proportionen

Das Pentagonikositetraeder: Der Pentagon-Körper mit Tribonacci-Harmonie

Das Pentagonikositetraeder ist ein außergewöhnlicher katalanischer Körper, der sich durch seine einzigartige Kombination aus pentagonalen Flächen und der faszinierenden Tribonacci-Konstante auszeichnet. Mit seinen 24 unregelmäßigen Fünfecksflächen stellt es einen seltenen Fall unter den katalanischen Körpern dar, bei dem pentagonale Geometrie dominiert. Als dualer Körper zum abgeschrägten Hexaeder verkörpert es eine bemerkenswerte Synthese aus kubischer Grundstruktur und pentagonaler Oberflächenkomplexität, wobei alle seine Proportionen und Beziehungen durch die geheimnisvolle Tribonacci-Konstante t ≈ 1.839 bestimmt werden, die eine natürliche Erweiterung der bekannteren Fibonacci-Folge darstellt.

Die pentagonale Harmonie der 24 Fünfecksflächen

Das Pentagonikositetraeder fasziniert durch seine pentagonale Perfektion:

  • 24 Fünfecksflächen: Jede Fläche ist ein unregelmäßiges Pentagon mit charakteristischen Tribonacci-Proportionen
  • Pentagonale Einzigartigkeit: Einer der wenigen katalanischen Körper mit Fünfecksflächen
  • Zwei Kantenlängen: Lange Kante (a) und kurze Kante (b) im Tribonacci-Verhältnis
  • Kompakte Struktur: 38 Ecken in optimaler pentagonaler Anordnung
  • Tribonacci-Geometrie: Alle Proportionen basieren auf t ≈ 1.839 und s ≈ 0.42
  • Perfekte Tessellation: Die 24 Fünfecke fügen sich harmonisch zusammen
  • Dualitätsprinzip: Jede Fünfecksfläche entspricht einer Ecke des abgeschrägten Hexaeders

Katalanische Tradition und pentagonale Dualität

Katalanische Besonderheit

Als einer der wenigen katalanischen Körper mit Fünfecksflächen nimmt das Pentagonikositetraeder eine Sonderstellung ein. Es zeigt, wie aus einer kubischen Grundstruktur pentagonale Komplexität entstehen kann.

Pentagon-Dualität

Als Dual zum abgeschrägten Hexaeder (einem der komplexeren uniformen Polyeder) vertauscht es systematisch kubische Struktur mit pentagonaler Oberflächengestaltung, wobei die Tribonacci-Konstante die Transformation bestimmt.

Geometrische Eleganz

Mit 24 Flächen erreicht es eine bemerkenswerte Balance zwischen Übersichtlichkeit und pentagonaler Komplexität, die es zu einem idealen Studienobjekt für Fünfeck-Geometrie macht.

Tribonacci-Eleganz

Die Formeln zeigen elegante Tribonacci-Beziehungen, die das Verständnis dieser weniger bekannten, aber faszinierenden mathematischen Konstante fördern und vertiefen.

Die Tribonacci-Konstante in pentagonaler Geometrie

Das Pentagonikositetraeder ist durchdrungen von Tribonacci-Beziehungen:

Tribonacci-Proportionen

Die Tribonacci-Konstante t ≈ 1.839 und der Parameter s = (t-1)/2 ≈ 0.42 bestimmen alle geometrischen Verhältnisse des Polyeders. Diese Konstante entsteht aus einer Verallgemeinerung der Fibonacci-Folge auf drei Terme.

Tribonacci-Formeln

Alle geometrischen Formeln enthalten den Parameter s in verschiedenen Kombinationen, was die fundamentale Rolle der Tribonacci-Konstante in der pentagonalen Geometrie dieses einzigartigen Polyeders unterstreicht.

Pentagonale Harmonie

Die Anordnung der 24 Fünfecksflächen folgt den Gesetzen der Tribonacci-Sequenz, wodurch jede Fläche in perfekter mathematischer Harmonie mit allen anderen steht und eine bemerkenswerte strukturelle Einheit entsteht.

Mathematische Raffinesse

Die Tribonacci-Organisation ermöglicht eine elegante mathematische Beschreibung bei gleichzeitiger Beibehaltung der charakteristischen Pentagon-Eigenschaften jeder einzelnen Fläche.

Wissenschaftliche und kulturelle Bedeutung

Das Pentagonikositetraeder findet Anwendung in spezialisierten Bereichen:

  • Pentagonale Kristallographie: Modell für Kristallstrukturen mit Fünfeck-Symmetrien
  • Tribonacci-Forschung: Physisches Modell für Tribonacci-Sequenz-Studien
  • Quasikristall-Forschung: Verbindung zu pentagonalen Quasikristallstrukturen
  • Geometrische Kunst: Inspiration für pentagonale Kunstwerke und Skulpturen
  • Bildung: Demonstration pentagonaler Geometrie und Tribonacci-Mathematik
  • Algorithmus-Entwicklung: Tests für Pentagon-Tessellations-Algorithmen
  • Materialwissenschaft: Template für pentagonale Strukturmaterialien

Konstruktion und pentagonale Präzision

Pentagonale Präzision

Die Herstellung erfordert höchste Präzision bei der Einhaltung der Tribonacci-Proportionen. Jede der 24 Fünfecksflächen muss exakte Winkel und Kantenverhältnisse aufweisen, die durch irrationale Tribonacci-Zahlen definiert sind.

Tribonacci-Herausforderungen

Die Tribonacci-Konstante ist weniger bekannt als der goldene Schnitt, was die Fertigung zu einer besonderen mathematischen und technischen Herausforderung macht, die spezielles Fachwissen erfordert.

Qualitätskontrolle

Die Überprüfung der pentagonalen Geometrie und Tribonacci-Proportionen erfordert spezialisierte Messverfahren und ein tiefes Verständnis der zugrunde liegenden Mathematik.

Moderne Fertigung

Hochpräzise CNC-Maschinen und spezialisierte Software können die komplexen Tribonacci-Beziehungen umsetzen, wodurch hochwertige Modelle für Forschung und Bildung realisierbar werden.

Ästhetische und pädagogische Dimensionen

Pentagonale Ästhetik

Die Kombination aus pentagonaler Vielfalt und Tribonacci-Harmonie erzeugt eine einzigartige ästhetische Wirkung, die sowohl mathematische Raffinesz als auch natürliche Eleganz ausstrahlt.

Pädagogischer Wert

Als seltenes Beispiel für pentagonale katalanische Körper und Tribonacci-Geometrie ist es ideal geeignet, um Studenten fortgeschrittene mathematische Konzepte näherzubringen.

Symbolische Bedeutung

In der Designphilosophie symbolisiert es die Harmonie zwischen natürlicher Pentagonalität und mathematischer Tribonacci-Ordnung, zwischen organischer Form und rationaler Struktur.

Kulturelle Relevanz

Als Vertreter der pentagonalen Familie geometrischer Formen verbindet es sich mit kulturellen Traditionen, die Fünfeck-Symmetrien und deren natürliche Schönheit schätzen.

Zusammenfassung

Das Pentagonikositetraeder verkörpert die faszinierende Synthese aus pentagonaler Geometrie und Tribonacci-Mathematik. Mit seinen 24 unregelmäßigen Fünfecksflächen, die in perfekter Tribonacci-Harmonie angeordnet sind, zeigt es, wie fortgeschrittene mathematische Konzepte geometrische Schönheit von bemerkenswerter Einzigartigkeit erzeugen können. Die durchgängigen Tribonacci-Beziehungen verbinden es mit einer weniger bekannten, aber ebenso faszinierenden mathematischen Tradition und machen es zu einem idealen Studienobjekt für die Erforschung von Pentagon-Geometrie, Tribonacci-Sequenzen und den subtilen Prinzipien der dreidimensionalen Harmonie. Von seiner theoretischen Bedeutung in der reinen Mathematik bis zu seinen praktischen Anwendungen in Quasikristall-Forschung und pentagonaler Kunst bleibt das Pentagonikositetraeder ein einzigartiges Beispiel dafür, wie seltene mathematische Strukturen sowohl intellektuelle Faszination als auch ästhetische Inspiration bieten können.

Deltoidalhexakontaeder • Deltoidalikositetraeder • Hexakisikosaeder • Hexakisoktaeder • Pentagonikositetraeder • Pentakisdodekaeder • Rhombendodekaeder • Rhombentriakontaeder • Tetrakishexaeder • Triakisikosaeder • Triakisoktaeder • Triakistetraeder