Kite Area Calculator

Calculator and formulas to calculate the area of a kite (deltoid)

Kite Area Calculator

The Kite (Deltoid)

A kite is a quadrilateral with two pairs of adjacent equal sides and one axis of symmetry along a diagonal.

Enter Diagonal Lengths

Note: Enter the lengths of both diagonals e and f

Diagonal e

Length of diagonal e

Diagonal f

Length of diagonal f

Decimal Places

Kite Properties

Symmetry: One diagonal is the axis of symmetry

Diagonal e Diagonal f A = (e·f)/2

Kite Area Result

Area A:

The area is half the product of the diagonals

Kite Structure

A kite has two pairs of adjacent equal sides.
The diagonals intersect at right angles.

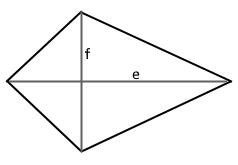
● Diagonal e (vertical) ● Diagonal f (horizontal)

What is a Kite?

A kite (also called deltoid) is a special quadrilateral with unique symmetry properties:

Definition: Quadrilateral with two pairs of adjacent equal sides
Symmetry axis: One diagonal is the axis of symmetry
Perpendicular diagonals: The two diagonals intersect at right angles (90°)

Convex form: Classic kite shape, all interior angles < 180°
Equal sides: Two pairs of adjacent sides are equal
Simple area formula: Half the product of the diagonals

Geometric Properties of the Kite

The kite possesses special geometric properties:

Side Properties

Two pairs of equal sides: AB = AD and CB = CD
Adjacent equality: Equal sides are adjacent (next to each other)
Four vertices: Points A, B, C, D form the kite
Convex shape: All interior angles less than 180°

Diagonal Properties

Perpendicular intersection: Diagonals meet at 90°
Symmetry axis: One diagonal (e) is the axis of symmetry
Bisection: Symmetry diagonal (e) bisects the other diagonal (f)
Area relation: Area = (e × f) / 2

Mathematical Relationships

The kite follows precise mathematical formulas:

Area Calculation

A = (e · f) / 2

The kite area is half the product of the two diagonal lengths. This simple formula works because the diagonals are perpendicular.

Perimeter Calculation

U = 2(a + b)

The perimeter is twice the sum of the two different side lengths. Since we have two pairs of equal sides, the formula simplifies nicely.

Applications of Kites

Kite shapes appear in various practical applications:

Aviation & Recreation

Flying kites and sport kites
Hang gliders and paragliders
Kite surfing and kite boarding
Wind power generation kites

Design & Art

Jewelry design and gemstone cuts
Tile patterns and mosaics
Logos and graphic design
Quilting and textile patterns

Architecture

Floor plan layouts
Window and door designs
Decorative elements
Structural frameworks

Science & Mathematics

Crystallography and mineral structures
Molecular geometry
Geometric proofs and theorems
Symmetry studies

Formulas for the Kite

Area A

\[A = \frac{e \cdot f}{2}\]

Area = half the product of diagonal lengths

Perimeter U

\[U = 2 \cdot a + 2 \cdot b = 2(a + b)\]

Sum of all four sides (two pairs of equal sides)

Diagonal Relation

\[e \perp f\]

Diagonals intersect at right angles (90°)

Side Lengths from Diagonals

\[a = \sqrt{\left(\frac{e}{2}\right)^2 + \left(\frac{f}{2}\right)^2}\]

Using Pythagorean theorem with half-diagonals

Symmetry Property

\[AB = AD \quad \text{and} \quad CB = CD\]

Two pairs of adjacent equal sides

Alternative Area Formula

\[A = a \cdot b \cdot \sin(\alpha)\]

Using sides and included angle

Calculation Example for a Kite

Given

Diagonal e = 6 Diagonal f = 4

Find: Area of the kite

1. Apply Area Formula

\[A = \frac{e \cdot f}{2}\] \[A = \frac{6 \cdot 4}{2}\]

Insert the diagonal values

2. Calculate Product

\[A = \frac{24}{2}\] \[A = 12\]

Multiply and divide

3. Verify with Geometry

\[\text{Kite divides into 4 right triangles}\] \[\text{Each triangle: } \frac{1}{2} \cdot 3 \cdot 2 = 3\] \[4 \times 3 = 12 \checkmark\]

Alternative verification method

4. Understanding the Result

\[\text{Rectangle area } = e \times f = 24\] \[\text{Kite area } = \frac{24}{2} = 12\] \[\text{(Half the rectangle)}\]

Kite is half of bounding rectangle

5. Complete Solution

Given: e = 6, f = 4

Result: A = 12 square units

Note: The kite area formula A = (e·f)/2 is remarkably simple because the diagonals are perpendicular!

6. More Examples

e=8, f=6

A = 24

e=10, f=8

A = 40

e=5, f=5

A = 12.5

Different diagonal combinations

The Kite: Symmetry and Elegance

The kite (deltoid) is a fascinating quadrilateral that combines symmetry with simplicity. Its defining characteristic — two pairs of adjacent equal sides — leads to elegant geometric properties and straightforward area calculations.

Definition and Core Properties

The kite is characterized by its unique structure:

Adjacent equality: Two pairs of consecutive sides are equal (AB = AD and CB = CD)
Single symmetry axis: One diagonal serves as the axis of symmetry
Perpendicular diagonals: The diagonals meet at exactly 90 degrees
Bisecting property: The symmetry diagonal bisects the other diagonal
Special angles: Two pairs of equal opposite angles

The Elegant Area Formula

The kite's area formula is remarkably simple:

Why A = (e·f)/2 Works

Because the diagonals are perpendicular, they divide the kite into four right triangles. The total area equals half the area of the rectangle formed by the diagonals.

Geometric Insight

If you draw both diagonals, they form a rectangle. The kite occupies exactly half of this rectangle's area — a beautiful geometric relationship!

Universal Application

This formula works for any kite, regardless of its proportions. You only need the two diagonal lengths — no angles or side lengths required!

Comparison to Other Quadrilaterals

The formula A = (d₁·d₂)/2 also works for rhombuses (a special case of kites) and squares (when both diagonals are equal), showing the kite's central role.

Kites in Nature and Culture

The kite shape appears throughout human history:

Historical Flying Kites

Flying kites have existed for over 2,000 years, originating in China. The diamond kite shape provides excellent aerodynamic stability and lift.

Crystallography

Many crystal structures exhibit kite-shaped cross-sections. The perpendicular diagonals reflect molecular symmetry axes.

Art and Design

Kite shapes appear in Islamic geometric patterns, modern logos, and architectural elements. The symmetry creates visual harmony.

Modern Applications

Today, kite shapes are used in everything from kitesurfing equipment to power-generating wind kites and even diamond cuts in jewelry.

Mathematical Relationships

The kite connects to broader mathematical concepts:

Special case of trapezoid: When one pair of sides becomes parallel
Related to rhombus: A rhombus is a kite with all four sides equal
Tangential quadrilateral: All kites have an inscribed circle
Cyclic kite: Some kites can be inscribed in a circle (squares)
Tessellation: Certain kites can tile the plane in interesting patterns
Convexity: Standard kites are convex; dart shapes are concave kites

Related Geometric Shapes

The kite family includes several important variants:

Rhombus (Diamond)

When all four sides of a kite are equal, it becomes a rhombus. All rhombuses are kites, but not all kites are rhombuses.

Square

A square is a rhombus with equal diagonals and right angles. It's the most symmetric kite possible.

Dart (Concave Kite)

An "arrowhead" shape where one interior angle exceeds 180°. Still has the same area formula!

Right Kite

A kite with two right angles. Common in roof designs and architectural features.

More Kite Formulas

For comprehensive kite calculations including perimeter, sides, and angles, visit the complete Kite Calculator.

Is this page helpful?

Thank you for your feedback!

Sorry about that
How can we improve it?

Square • Rectangle • Golden Rectangle • Rectangle to Square • Rhombus, given varios parameter • Rhombus , given diagonal e, f • Parallelogram, given 2 sides and angle • Parallelogram area, given side and height • Trapezoid • Cyclic Quadrilateral • General Quadrilateral • Concave Quadrilateral • Arrowhead Quadrilateral • Crossed Square • Frame • Kite, given 2 diagonal and distance • Kite Area, given 2 diagonal • Half Square Kite • Right Kite"