Kite Calculator

Calculator and formulas for calculating the parameters of a kite (deltoid)

Kite Calculator

The Kite (Deltoid)

A kite is a quadrilateral with two pairs of adjacent equal sides and perpendicular diagonals.

Enter Parameters
Input: Enter the diagonals e, f and distance c
Symmetry diagonal (vertical)
Cross diagonal (horizontal)
Distance from A to intersection
Kite Properties

Key Features: Two pairs of adjacent equal sides

Diagonal e Diagonal f e ⊥ f
Kite Calculation Results
Side a:
Side b:
Perimeter:
Area A:
Angle α:
Angle β:
Angle γ:
The diagonals are perpendicular (e ⊥ f)

Kite Structure

A kite has two pairs of adjacent equal sides.
The diagonals intersect at right angles.

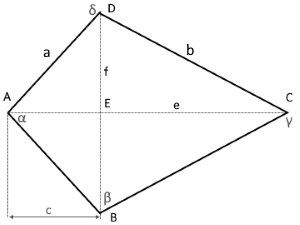
Kite Diagram

● Diagonal e (symmetry axis) ● Diagonal f


What is a Kite?

A kite (also called deltoid) is a special quadrilateral with unique symmetry properties:

  • Definition: Quadrilateral with two pairs of adjacent equal sides
  • Symmetry axis: One diagonal (e) is the axis of symmetry
  • Perpendicular diagonals: The two diagonals intersect at right angles (90°)
  • Convex form: Classic kite shape, all interior angles < 180°
  • Equal sides: AB = AD and CB = CD (two pairs)
  • Equal angles: Angles at B and D are equal (β = δ)

Geometric Properties of the Kite

The kite possesses special geometric properties:

Side Properties
  • Two pairs of equal sides: AB = AD and CB = CD
  • Adjacent equality: Equal sides are adjacent (next to each other)
  • Four vertices: Points A, B, C, D form the kite
  • Convex shape: All interior angles less than 180°
Diagonal Properties
  • Perpendicular intersection: Diagonals meet at 90°
  • Symmetry axis: Diagonal e is the axis of symmetry
  • Bisection: Symmetry diagonal e bisects diagonal f
  • Area relation: Area = (e × f) / 2

Mathematical Relationships

The kite follows precise mathematical formulas:

Area Calculation
A = (e · f) / 2

The kite area is half the product of the two diagonal lengths. This simple formula works because the diagonals are perpendicular.

Perimeter Calculation
P = 2(a + b)

The perimeter is twice the sum of the two different side lengths. Since we have two pairs of equal sides, the formula simplifies nicely.

Formulas for the Kite

Side length a
\[a = \sqrt{\left(\frac{f}{2}\right)^2 + c^2}\]

Using Pythagorean theorem with half diagonal and distance c

Side length b
\[b = \sqrt{\left(\frac{f}{2}\right)^2 + (e-c)^2}\]

Using Pythagorean theorem with remaining segment

Area A
\[A = \frac{e \cdot f}{2} = a \cdot b \cdot \sin(\beta)\]

Half the product of diagonals, or using sides and angle

Perimeter P
\[P = 2a + 2b = 2(a + b)\]

Sum of all four sides

Diagonal e
\[e = \sqrt{a^2 + b^2 - 2ab\cos(\beta)}\]

Using law of cosines

Diagonal f
\[f = 2a\sin\left(\frac{\alpha}{2}\right) = 2b\sin\left(\frac{\gamma}{2}\right)\]

Using sine of half angles

Angle α
\[\alpha = \arccos\left(\frac{2a^2 - f^2}{2a^2}\right)\]

Angle at vertex A

Angle γ
\[\gamma = \arccos\left(\frac{2b^2 - f^2}{2b^2}\right)\]

Angle at vertex C

Angles β and δ
\[\beta = \delta = \arccos\left(\frac{a^2 + b^2 - e^2}{2ab}\right)\]

Equal angles at vertices B and D

Perpendicularity
\[e \perp f\]

Diagonals are perpendicular (90°)

Calculation Example for a Kite

Given
Diagonal e = 5 Diagonal f = 4 Distance c = 2

Find: All properties of the kite

1. Calculate Side a
\[a = \sqrt{\left(\frac{f}{2}\right)^2 + c^2}\] \[a = \sqrt{\left(\frac{4}{2}\right)^2 + 2^2}\] \[a = \sqrt{4 + 4} = \sqrt{8} = 2.83\]

Side a using Pythagorean theorem

2. Calculate Side b
\[b = \sqrt{\left(\frac{f}{2}\right)^2 + (e-c)^2}\] \[b = \sqrt{2^2 + (5-2)^2}\] \[b = \sqrt{4 + 9} = \sqrt{13} = 3.61\]

Side b using remaining segment

3. Calculate Area
\[A = \frac{e \cdot f}{2}\] \[A = \frac{5 \times 4}{2}\] \[A = \frac{20}{2} = 10\]

Area using diagonal formula

4. Calculate Perimeter
\[P = 2(a + b)\] \[P = 2(2.83 + 3.61)\] \[P = 2 \times 6.44 = 12.88\]

Total perimeter of the kite

5. Calculate Angle α
\[\alpha = \arccos\left(\frac{2 \times 2.83^2 - 4^2}{2 \times 2.83^2}\right)\] \[\alpha = \arccos\left(\frac{16 - 16}{16}\right)\] \[\alpha = \arccos(0) = 90°\]

Angle at vertex A

6. Calculate Angle γ
\[\gamma = \arccos\left(\frac{2 \times 3.61^2 - 4^2}{2 \times 3.61^2}\right)\] \[\gamma = \arccos\left(\frac{26.06 - 16}{26.06}\right)\] \[\gamma \approx 67.4°\]

Angle at vertex C

7. Summary of Results
a = 2.83 b = 3.61
P = 12.88 A = 10
α = 90° γ ≈ 67.4°

Complete properties of a kite with diagonals e=5, f=4, and distance c=2

Applications of Kites

Kite shapes appear in various practical applications:

Aviation & Recreation
  • Flying kites and sport kites
  • Hang gliders and paragliders
  • Kite surfing and kite boarding
  • Wind power generation kites
Design & Art
  • Jewelry design and gemstone cuts
  • Tile patterns and mosaics
  • Logos and graphic design
  • Quilting and textile patterns
Architecture
  • Floor plan layouts
  • Window and door designs
  • Decorative elements
  • Structural frameworks
Science & Mathematics
  • Crystallography and mineral structures
  • Molecular geometry
  • Geometric proofs and theorems
  • Symmetry studies

The Kite: Symmetry and Elegance

The kite (deltoid) is a fascinating quadrilateral that combines symmetry with simplicity. Its defining characteristic — two pairs of adjacent equal sides — leads to elegant geometric properties and straightforward area calculations.

Definition and Core Properties

The kite is characterized by its unique structure:

  • Adjacent equality: Two pairs of consecutive sides are equal (AB = AD and CB = CD)
  • Single symmetry axis: One diagonal serves as the axis of symmetry
  • Perpendicular diagonals: The diagonals meet at exactly 90 degrees
  • Bisecting property: The symmetry diagonal bisects the other diagonal
  • Special angles: Two pairs of equal opposite angles

The Elegant Area Formula

The kite's area formula is remarkably simple:

Why A = (e·f)/2 Works

Because the diagonals are perpendicular, they divide the kite into four right triangles. The total area equals half the area of the rectangle formed by the diagonals.

Geometric Insight

If you draw both diagonals, they form a rectangle. The kite occupies exactly half of this rectangle's area — a beautiful geometric relationship!

Universal Application

This formula works for any kite, regardless of its proportions. You only need the two diagonal lengths — no angles or side lengths required!

Comparison to Other Quadrilaterals

The formula A = (d₁·d₂)/2 also works for rhombuses (a special case of kites) and squares (when both diagonals are equal), showing the kite's central role.

Kites in Nature and Culture

The kite shape appears throughout human history:

Historical Flying Kites

Flying kites have existed for over 2,000 years, originating in China. The diamond kite shape provides excellent aerodynamic stability and lift.

Crystallography

Many crystal structures exhibit kite-shaped cross-sections. The perpendicular diagonals reflect molecular symmetry axes.

Art and Design

Kite shapes appear in Islamic geometric patterns, modern logos, and architectural elements. The symmetry creates visual harmony.

Modern Applications

Today, kite shapes are used in everything from kitesurfing equipment to power-generating wind kites and even diamond cuts in jewelry.

Mathematical Relationships

The kite connects to broader mathematical concepts:

  • Special case of trapezoid: When one pair of sides becomes parallel
  • Related to rhombus: A rhombus is a kite with all four sides equal
  • Tangential quadrilateral: All kites have an inscribed circle
  • Cyclic kite: Some kites can be inscribed in a circle (squares)
  • Tessellation: Certain kites can tile the plane in interesting patterns
  • Convexity: Standard kites are convex; dart shapes are concave kites

Related Geometric Shapes

The kite family includes several important variants:

Rhombus (Diamond)

When all four sides of a kite are equal, it becomes a rhombus. All rhombuses are kites, but not all kites are rhombuses.

Square

A square is a rhombus with equal diagonals and right angles. It's the most symmetric kite possible.

Dart (Concave Kite)

An "arrowhead" shape where one interior angle exceeds 180°. Still has the same area formula!

Right Kite

A kite with two right angles. Common in roof designs and architectural features.

Summary

The kite exemplifies how geometric constraints create elegant properties. Its requirement for adjacent equal sides naturally produces perpendicular diagonals, which in turn yield the beautiful area formula A = (e·f)/2. From ancient flying kites to modern engineering, this simple quadrilateral demonstrates that mathematical beauty and practical utility often go hand in hand. The kite reminds us that symmetry and simplicity can produce both aesthetic appeal and functional excellence.

Is this page helpful?            
Thank you for your feedback!

Sorry about that

How can we improve it?

Square • Rectangle • Golden Rectangle • Rectangle to Square • Rhombus, given varios parameter • Rhombus , given diagonal e, f • Parallelogram, given 2 sides and angle • Parallelogram area, given side and height • Trapezoid • Cyclic Quadrilateral • General Quadrilateral • Concave Quadrilateral • Arrowhead Quadrilateral • Crossed Square • Frame • Kite, given 2 diagonal and distance • Kite Area, given 2 diagonal • Half Square Kite • Right Kite"