Parallelogram Area Calculator
Calculator and formulas to compute the area of a parallelogram
Parallelogram Calculator
Parallelogram Area Calculation
A parallelogram has parallel opposite sides and the area A = base × height. Simple and accurate calculation.
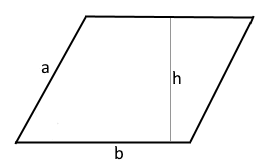
Parallelogram Visualization
The diagram shows a parallelogram with base b and height h.
The area is calculated as A = b × h.
|
|
What is a parallelogram?
A parallelogram is a quadrilateral with the following properties:
- Parallel sides: Opposite sides are parallel
- Equal opposite sides: Opposite sides have equal length
- Equal opposite angles: Opposite angles are equal
- Area: A = base × height
- Height: Perpendicular distance between parallel sides
- Applications: Engineering, architecture, physics
Parallelogram properties
The parallelogram has characteristic geometric properties:
Sides and angles
- Opposite sides are parallel and equal in length
- Opposite angles are equal
- Adjacent angles add up to 180°
- Total angle sum is 360°
Diagonals
- Diagonals bisect each other
- Diagonals divide the parallelogram into 4 triangles
- Opposite triangles are congruent
- Diagonals are not generally equal in length
Understanding area calculation
The area calculation of the parallelogram is based on a simple principle:
The basic principle
- Base b: one of the parallel sides
- Height h: perpendicular distance to the base
- Formula: A = b × h
- Height is not equal to the side length unless rectangle
Why it works
- A parallelogram can be sheared into a rectangle
- The area is preserved under shear transformations
- Rectangle area = length × width
- Matches base × height of the parallelogram
Applications of parallelograms
Parallelograms appear in many practical areas:
Architecture & Construction
- Roof structures and beams
- Window and door frames
- Facade elements
- Stairs and ramps
Mechanical engineering & Technology
- Gears and mechanisms
- Parallelogram linkages
- Scissor lifts
- Pantograph constructions
Design & Art
- Graphic design
- Logos and corporate design
- Patterns and ornaments
- Contemporary architecture
Mathematics & Physics
- Vector representation
- Parallelogram of forces
- Coordinate transformations
- Lattice structures
Formulas for the parallelogram
Area A
Base times height (perpendicular distance)
Base from area
Calculate base when area and height are known
Height from area
Calculate height when area and base are known
Alternative area formula
Using side lengths a, b and included angle α
Important notes
- b: Base (one of the sides)
- h: Height (perpendicular to the base)
- A: Area
- α: Angle between sides
- Height ≠ side length (except for rectangle)
- Height: Always perpendicular to the chosen base
Example calculation for a parallelogram
Given
Find: area of the parallelogram
1. Apply formula
Simple multiplication of base and height
2. Interpret result
The parallelogram has an area of 40 units²
3. Check and understanding
Reverse checks confirm our result
The parallelogram: fundamental geometric shape
The parallelogram is one of the most important and versatile geometric shapes. It combines mathematical elegance with practical applicability and forms the basis for understanding more complex geometric structures and physical principles.
Mathematical basics and properties
The mathematical properties of the parallelogram are diverse and elegant:
- Parallelism: Opposite sides are parallel and equal in length
- Angle properties: Opposite angles are equal, adjacent angles are supplementary
- Diagonals: Intersect at their midpoint and bisect each other
- Symmetry: Point symmetry about the intersection of diagonals
- Area formula: A = base × height (independent of skew)
- Vector representation: Ideal for representing vectors
Understanding the area formula
The area formula A = b × h is more elegant than it may first appear:
Geometric intuition
Any parallelogram can be transformed (sheared) into a rectangle with the same base and height. The area remains unchanged under shear transformations.
Height vs side length
The height is the perpendicular distance between the parallel sides, not the length of an oblique side. This is a common source of confusion.
Sine alternative
The alternative A = a × b × sin(α) shows the connection to vector geometry. The sine factor converts a side length into the effective height.
Invariance under shear
The area remains the same regardless of how much the parallelogram is sheared, as long as base and height are preserved.
Applications in science and engineering
Parallelograms are fundamental in many fields:
- Mechanics: Parallelogram of forces for vector addition
- Mechanical engineering: Parallelogram linkages for guided motion
- Crystallography: Unit cells in crystal lattices
- Computer graphics: Affine transformations and shearing
- Architecture: Structural elements and load distribution
- Navigation: Coordinate systems and map projections
Special parallelograms and relatives
The parallelogram is the superclass of several special quadrilaterals:
Rectangle
A parallelogram with four right angles. Here height equals side length and area calculation is simpler.
Rhombus
A parallelogram with four equal sides. Area often computed via diagonals: A = (d₁ × d₂)/2.
Square
Both rectangle and rhombus - the perfect form with maximal symmetry and area formula A = a².
Rhomboid
General term for oblique parallelograms without right angles or equal sides - the most basic skew form.
Summary
The parallelogram illustrates beautiful geometric principles: from simple properties (parallel sides) emerge elegant relationships and practical applications. The area formula A = b × h embodies the principle of geometric invariance - area stays constant when base and height are preserved. From basic vector geometry to complex engineering applications, the parallelogram remains a fundamental tool for understanding geometric space.
|
|
|
|