Calculate parallelogram

Calculator and formulas for the rhomboid with parallel sides

Parallelogram calculator

The parallelogram (rhomboid)

A parallelogram has two pairs of parallel sides with opposite equal angles.

Enter side lengths and angle
First parallel side
Second parallel side
Acute interior angle
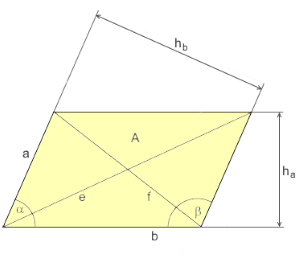
Parallelogram results
Area A:
Perimeter P:
Height ha:
Height hb:
Diagonal e:
Diagonal f:
Angle β:

Parallelogram structure

Parallelogram properties

Remark: Opposite sides are parallel and equal, α + β = 180°

a ∥ c, b ∥ d |a| = |c|, |b| = |d| α = γ, β = δ

The parallelogram with parallel sides a∥c and b∥d.
Opposite angles are equal: α = γ, β = δ.

Parallelogram

The parallelogram: elegance of parallel lines

The parallelogram (rhomboid) is a fundamental geometric quadrilateral:

  • Parallel sides: a ∥ c and b ∥ d (two side pairs)
  • Equal lengths: |a| = |c| and |b| = |d|
  • Supplementary angles: α + β = 180° (adjacent angles)
  • Equal opposite angles: α = γ and β = δ
  • Diagonals bisect each other: Intersection is the center
  • Height relation: A = a · hb = b · ha

Geometric properties of the parallelogram

The special properties of the parallelogram make it very versatile:

Parallelism and symmetry
  • Two pairs of parallel sides
  • Point-symmetric with respect to the diagonal intersection
  • Opposite sides have equal length
  • No mirror symmetry (except rectangle/rhombus)
Angle properties
  • Opposite angles are equal
  • Adjacent angles are supplementary (180°)
  • Angle sum: α + β + γ + δ = 360°
  • Only two distinct angle measures

Mathematical calculations in the parallelogram

Calculation methods for parallelograms are varied and elegant:

Area calculations
  • A = a · h_b = b · h_a (base × height)
  • A = a · b · sin(α) (sides × sine)
  • Heights: h_a = b · sin(α), h_b = a · sin(α)
  • Three equivalent calculation methods
Diagonal calculations
  • Law of cosines for both diagonals
  • e = √(a² + b² - 2ab·cos(β))
  • f = √(a² + b² - 2ab·cos(α))
  • Diagonals bisect each other

Applications of the parallelogram

Parallelograms have many practical applications:

Architecture & construction
  • Roof constructions using parallelogram shapes
  • Truss structures and bracing
  • Skewed window and door frames
  • Modern building geometries
Engineering & mechanical design
  • Gear and transmission linkages
  • Parallelogram linkages in mechanisms
  • Pantograph systems (current collectors)
  • Windshield wiper mechanisms
Design & art
  • Graphic design and layout composition
  • Typography (italic fonts)
  • Logo design with dynamic shapes
  • Architectural visualization
Physics & mathematics
  • Force parallelogram in mechanics
  • Vector addition and decomposition
  • Coordinate transformations
  • Crystallography (lattice structures)

Formulas for the parallelogram

Area A
\[A = b \cdot h_a = a \cdot h_b = a \cdot b \cdot \sin(\alpha)\]

Three equivalent calculation methods

Perimeter P
\[P = 2 \cdot (a + b)\]

Double sum of adjacent sides

Heights h_a and h_b
\[h_a = \frac{A}{b} = a \cdot \sin(\alpha)\] \[h_b = \frac{A}{a} = b \cdot \sin(\alpha)\]

Heights from area or trigonometry

Diagonals e and f
\[e = \sqrt{a^2 + b^2 - 2ab \cos(\beta)}\] \[f = \sqrt{a^2 + b^2 - 2ab \cos(\alpha)}\]

Law of cosines for both diagonals

Side lengths from area
\[a = \frac{A}{h_b} = \frac{A}{b \cdot \sin(\alpha)}\] \[b = \frac{A}{h_a} = \frac{A}{a \cdot \sin(\alpha)}\]

Back-calculation of sides

Angle α from area
\[\alpha = \arcsin\left(\frac{A}{a \cdot b}\right)\]

Compute angle from given area

Angle relations
\[\alpha + \beta = 180° \quad\text{and}\quad \alpha = \gamma, \beta = \delta\]

Supplementary adjacent angles, equal opposite angles

Worked example for a parallelogram

Given
Side a = 5 Side b = 3 Angle α = 60°

Find: All parameters of the parallelogram

1. Area and perimeter
\[A = 5 \times 3 \times \sin(60°) = 15 \times 0.866 = 12.99\] \[P = 2 \times (5 + 3) = 16\]

Area with sine formula, perimeter as side sum

2. Compute heights
\[h_a = 3 \times \sin(60°) = 3 \times 0.866 = 2.60\] \[h_b = 5 \times \sin(60°) = 5 \times 0.866 = 4.33\]

Heights via trigonometric relation

3. Angles and diagonals
β = 180° - 60° = 120° e = √(25 + 9 - 2×5×3×cos(120°)) = 7.00
f = √(25 + 9 - 2×5×3×cos(60°)) = 4.36 γ = α = 60°, δ = β = 120°

Supplementary angle β and diagonals via law of cosines

4. Complete parallelogram
Sides: a=5, b=3, c=5, d=3 Angles: α=60°, β=120°, γ=60°, δ=120°
Perimeter P = 16 Area A = 12.99 Heights: ha=2.60, hb=4.33 Diagonals: e=7.00, f=4.36

The complete parallelogram - elegant parallelism in practice!

The parallelogram: elegance of parallelism in geometry and engineering

The parallelogram stands as a fundamental geometric form expressing the principle of parallelism. With two pairs of parallel sides and the characteristic property that opposite sides and angles are equal, it embodies geometric harmony and has many applications from mechanics to modern architecture.

The beauty of parallel geometry

The parallelogram fascinates through its elegant properties:

  • Double parallelism: Two side pairs a∥c and b∥d create a stable structure
  • Symmetry of opposites: Opposite sides and angles are equal
  • Supplementary harmony: Adjacent angles sum to 180°
  • Central symmetry: Point-symmetric about the diagonal intersection
  • Triple area formula: A = a·hb = b·ha = a·b·sin(α)
  • Diagonal bisection: Both diagonals bisect each other

Parallelograms in nature and technology

Nature and human technology use parallelogram structures for stability and function:

Mechanical systems

Parallelogram linkages in vehicle technology ensure uniform movement. Pantographs on trains use this geometry for consistent contact with overhead lines.

Crystal structures

Many minerals form parallelogram-like lattice structures. This arrangement minimizes energy and maximizes structural stability.

Architecture and construction

Modern architecture uses parallelogram forms for dynamic building silhouettes. Truss constructions use this geometry for optimal load distribution.

Physics and forces

The force parallelogram is fundamental in mechanics. Vector addition and decomposition are based on parallelogram principles.

Mathematical elegance and calculation variety

The parallelogram offers remarkable mathematical flexibility:

  • Three area formulas: base×height, sides×sine, height-dependent variants
  • Trigonometric relations: Heights as h_a = b·sin(α), h_b = a·sin(α)
  • Law of cosines for diagonals: Both diagonals via a unified formula
  • Angle arithmetic: α + β = 180°, only two independent angles
  • Invertibility: All parameters computable from various inputs
  • Special cases: Rectangle (α = 90°) and rhombus (a = b) as special forms

Modern applications and future perspectives

The parallelogram gains new relevance in the digital era:

Computer Graphics

Parallelograms are building blocks for texture mapping and 3D transformations. Affine transforms preserve parallelism.

Robotics and automation

Parallelogram mechanisms in industrial robots provide precise, repeatable motion. Delta robots use this geometry for high-speed operations.

Architectural innovation

Parametric architecture uses parallelogram variations for adaptive facades. Smart buildings use this geometry for movable shading systems.

Material science

Metamaterials with parallelogram structures show special mechanical properties. Negative Poisson ratios emerge from clever parallelogram arrangements.

Parallelograms as a design principle

The parallelogram inspires modern design through its dynamic statics:

  • Visual Dynamics: Oblique angles create the illusion of movement in static objects
  • Typographic Design: Italic fonts are based on parallelogram principles
  • Logo Design: Parallelograms convey progress and dynamism
  • UI/UX Design: Oblique interface elements create modern aesthetics
  • Industrial Design: Parallelogram shapes suggest speed and efficiency
  • Architectural Identity: Parallelogram buildings become striking landmarks

Square • Rectangle • Golden Rectangle • Rectangle to Square • Rhombus, given varios parameter • Rhombus , given diagonal e, f • Parallelogram, given 2 sides and angle • Parallelogram area, given side and height • Trapezoid • Cyclic Quadrilateral • General Quadrilateral • Concave Quadrilateral • Arrowhead Quadrilateral • Crossed Square • Frame • Kite, given 2 diagonal and distance • Kite Area, given 2 diagonal • Half Square Kite • Right Kite"