Calculate rectangle
Calculator and formulas for the classic rectangle
Rectangle calculator
The rectangle
A rectangle has four right angles and opposite sides parallel.
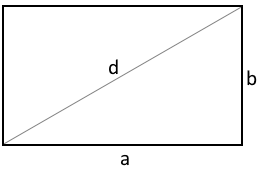
Rectangle structure
Rectangle properties
Base form: Four right angles, opposite sides equal
Rectangle with length a and width b.
All interior angles equal 90°.
|
|
The rectangle: foundation of right-angled geometry
The rectangle is the fundamental shape of right-angled geometry:
- Four right angles: Each interior angle = 90°
- Parallel sides: Opposite sides are parallel
- Equal opposite sides: a₁ = a₂ and b₁ = b₂
- Equal diagonals: Both diagonals have length d
- Diagonals bisect each other: Diagonals cut each other in half
- Circumcircle exists: Center at diagonals intersection
Geometric properties of the rectangle
The mathematical properties of the rectangle are clearly defined:
Angle properties
- All four interior angles are right angles (90°)
- Angle sum: 4 × 90° = 360°
- No acute or obtuse interior angles
- Perfect orthogonality at all side intersections
Side relations
- Opposite sides are equal in length
- Opposite sides are parallel
- Adjacent sides are perpendicular to each other
- Two distinct side lengths (usually a ≠ b)
Mathematics of rectangle calculation
The mathematical relations of the rectangle are elementary:
Area calculation
- Area: A = a × b (length times width)
- Simplest area formula among quadrilaterals
- Basis for more complex area computations
- Direct multiplication without trigonometry
Pythagorean relation
- Diagonal: d = √(a² + b²)
- Pythagorean theorem applicable
- Right triangles at the corners
- Diagonal as hypotenuse
Applications of the rectangle
Rectangles are omnipresent in our structured world:
Architecture & construction
- Floor plans and space planning
- Windows, doors and openings
- Facade design
- Structural frame systems
Digital world
- Screens and displays
- Website layout and UI design
- Pixel arrays and raster systems
- Windows and dialog boxes
Production & manufacturing
- Material cutting and planning
- Packaging design
- Mechanical components
- Electronics boards and housings
Art & design
- Canvases and picture frames
- Typography and layout design
- Furniture design and interior architecture
- Graphic grid systems
Formulas for the rectangle
Length a
Length from area and width
Width b
Width from area and length
Area A
Length times width - simplest area formula
Perimeter P
Double sum of both side lengths
Diagonal d
Pythagorean theorem - diagonal as hypotenuse
Worked example for a rectangle
Given
Find: All parameters of the rectangle
1. Compute area
Simple multiplication of the sides
2. Compute perimeter
Sum of all four side lengths
3. Diagonal with Pythagoras
Pythagorean theorem for right triangles
4. Complete rectangle
The classic 3-4-5 rectangle - a Pythagorean triple!
The rectangle: cornerstone of right-angled geometry
The rectangle stands as a fundamental form of geometry at the heart of human culture and technology. With its four right angles and parallel opposite sides it embodies order, structure and mathematical clarity. From ancient temples to modern displays and digital interfaces - the rectangle shapes our visual and structural world through its perfect balance of simplicity and functional versatility.
The mathematical purity of the rectangle
The rectangle embodies mathematical basic principles in their purest form:
- Right-angledness: Four perfect 90° angles without exception
- Parallelism: Opposite sides exactly parallel
- Equality of opposite sides: a₁ = a₂ and b₁ = b₂
- Pythagorean diagonal: d = √(a² + b²) - fundamental relation
- Simple area formula: A = a × b - no trigonometry required
- Circumcircle existence: Uniquely determined circumcircle center
The rectangle in cultural history
Culturally the rectangle has deep historical significance:
Ancient architecture
Greek temples and Roman basilicas used rectangular floor plans for stability and harmony. The golden ratio in rectangular proportions became an aesthetic norm.
Medieval urban planning
Roman castra and medieval town foundations followed rectangular grids. This order facilitated administration and defense.
Renaissance and modernity
Perspective and vanishing point constructions were based on rectangular coordinate systems. Bauhaus design elevated the rectangle to a design principle.
Digital revolution
Pixels, screens and user interfaces are fundamentally rectangular. The digital world is a world of rectangles.
Technical omnipresence of the rectangle
In modern technology the rectangle is ubiquitous:
- Display technology: Screens, smartphones, tablets - all rectangular
- Architectural systems: Modular construction and grid systems
- Electronics design: Boards, chips and housings follow rectangular standards
- Software interfaces: Windows, buttons and layout systems
- Production efficiency: Rectangular cuts minimize material waste
- Logistics optimization: Containers and packaging for maximal space use
Psychology and perception of rectangular forms
The impact of the rectangle on human perception is profound:
Cognitive processing
The human brain processes rectangular structures particularly efficiently. Rectangles are recognized and categorized faster than other shapes.
Order psychology
Rectangular arrangements convey order, stability and trust. They reduce cognitive load and promote clarity.
Cultural imprint
Western cultures associate rectangles with rationality and progress. They symbolize technical and societal development.
Design principles
Rectangular grids enable harmonious proportions and aesthetic balance. They are the foundation of modern typography and layout design.
Future perspectives of rectangle geometry
The future brings new applications for rectangular structures:
- Flexible displays: Foldable and bendable rectangular screens
- Smart buildings: Adaptive rectangular modules for transformable architecture
- Nano-structuring: Rectangular arrays at the molecular level
- Quantum computing: Rectangular qubit arrangements for stability
- Augmented reality: Rectangular overlays for spatial information
- Sustainable design: Modular rectangular systems for circular economy
Summary
The rectangle stands as a timeless symbol of order, clarity and functional perfection. Its four right angles and parallel sides embody the essence of structured thinking and rational design. From ancient architecture through the digital revolution to future technologies, the rectangle remains a fundamental building block of our visual and technical world. It reminds us that in apparent simplicity - four lines, four angles - infinite possibilities lie. The rectangle is not just a geometric shape but a cultural paradigm that creates order, enables efficiency and fosters aesthetic harmony.
|
|
|
|