Cyclic Quadrilateral Calculator
Calculator for quadrilaterals inscribed in a circle
Cyclic Quadrilateral Calculator
The cyclic quadrilateral
A cyclic quadrilateral is a quadrilateral whose vertices lie on a circumcircle. All sides are chords of the circle.
Cyclic quadrilateral in the circle
Cyclic properties
Ptolemy's theorem: e × f = a×c + b×d (diagonals relationship)
Cyclic quadrilateral inscribed in a circumcircle.
All vertices lie on the circle.
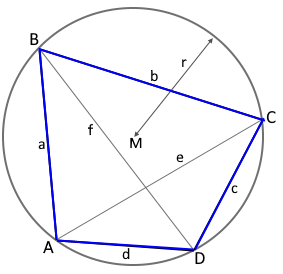
|
|
The cyclic quadrilateral: inscribed circle perfection
The cyclic quadrilateral is one of the most elegant geometric shapes:
- Circumcircle property: All vertices lie on a circle
- Chord sides: Each side is a chord of the circle
- Supplementary opposite angles: α + γ = β + δ = 180°
- Ptolemy's theorem: e × f = a×c + b×d
- Brahmagupta formula: A = √[(s-a)(s-b)(s-c)(s-d)]
- Unique determination: Four sides define everything
Special properties of cyclic quadrilaterals
The mathematical properties are determined by the circular layout:
Angle properties
- Opposite angles sum to 180°
- Inscribed angles over the same chord are equal
- Angle sum = 360° (as for all quadrilaterals)
- Unique angle determination from sides
Ptolemy's theorem
- Diagonal product: e × f = a×c + b×d
- Fundamental theorem for cyclic quadrilaterals
- Generalization of the Pythagorean theorem
- Basis for diagonal calculations
Mathematics of cyclic quadrilateral calculation
The mathematical relations use ancient and modern insights:
Brahmagupta formula (7th c.)
- A = √[(s-a)(s-b)(s-c)(s-d)]
- s = (a+b+c+d)/2 (semiperimeter)
- Generalization of Heron's formula
- Valid only for cyclic quadrilaterals
Ptolemy relations
- Diagonals from side ratios
- Complex root expressions
- Trigonometric angle calculations
- Circumcircle radius determination
Applications of the cyclic quadrilateral
Cyclic quadrilaterals find applications in various fields:
Ancient astronomy
- Ptolemaic astronomical calculations
- Planetary orbit approximations
- Calendar computations
- Trigonometric tables
Geometric construction
- Compass-and-straightedge constructions
- Architectural planning
- Gothic window rosettes
- Symmetric ornaments
Modern engineering
- Gear mechanisms
- Robot kinematics
- CAD system algorithms
- Computer graphics computations
Science
- Crystallography analyses
- Molecular geometry
- Optics and lens systems
- Geodesy and surveying
Formulas for the cyclic quadrilateral
Diagonals e and f
Complex diagonal formulas derived from Ptolemy's theorem
Brahmagupta area formula
Semiperimeter s and the famous area formula
Circumcircle radius r
Radius of the circumcircle through all vertices
Perimeter P
Simple sum of all side lengths
Angle relations
Opposite angles complement to 180° (characteristic for cyclic quadrilaterals)
Worked example for a cyclic quadrilateral
Given
Find: All parameters of the cyclic quadrilateral
1. Semiperimeter and area
Brahmagupta formula in action
2. Compute diagonals
Ptolemy-based diagonal calculation
3. Circumcircle and angles
Supplementary opposite angles confirmed: α + γ = β + δ = 180°
4. Complete cyclic quadrilateral
Fully determined cyclic quadrilateral satisfying all classical theorems!
The cyclic quadrilateral: bridge between antiquity and modernity
The cyclic quadrilateral unites the elegance of circle geometry with the complexity of multi-sided figures. This remarkable geometric shape connects ancient mathematical insights from Brahmagupta and Ptolemy with modern applications in engineering and science. As a quadrilateral whose vertices all lie on a circle, it embodies the harmonious connection between the perfect circle and the practical versatility of polygons.
The ancient roots of the cyclic quadrilateral
Mathematical investigation of cyclic quadrilaterals goes back more than 1400 years:
- Brahmagupta (628 AD): Developed the famous area formula for cyclic quadrilaterals
- Ptolemy (2nd c. AD): Formulated the fundamental theorem on diagonals
- Supplementary property: Opposite angles sum to 180°
- Unique determination: Four side lengths define the cyclic quadrilateral completely
- Maximal area: Among all quadrilaterals with given sides, the cyclic one has maximal area
- Circumcircle existence: Unique circumcircle through all four vertices
Mathematical depth and elegance
The cyclic quadrilateral displays remarkable mathematical beauty:
Brahmagupta formula
A = √[(s-a)(s-b)(s-c)(s-d)] generalizes Heron's formula for triangles. This elegant formula works only for cyclic quadrilaterals and reflects their special properties.
Ptolemy's theorem
The diagonal product e×f = ac + bd is a fundamental relation that holds only for cyclic quadrilaterals. It generalizes the Pythagorean theorem for non-right quadrilaterals.
Angle harmony
The supplementarity of opposite angles (α + γ = 180°) is characteristic and allows elegant trigonometric computations.
Extremal property
Among all quadrilaterals with given side lengths, the cyclic quadrilateral has the maximal area — an optimization principle of nature.
Applications in the modern world
Despite its ancient origins, the cyclic quadrilateral finds modern applications:
- Robotics and kinematics: Joint connections and motion mechanisms
- Computer-Aided Design: Algorithms for complex geometric constructions
- Architecture: Gothic window rosettes and symmetric ornaments
- Crystallography: Analysis of molecular structures and crystal lattices
- Optics: Lens systems and mirror arrangements
- Geodesy: Surveying techniques and triangulation
The cyclic quadrilateral in mathematical research
Modern mathematical research expands our understanding:
Complex analysis
Cyclic quadrilaterals in the complex plane show fascinating properties regarding conformal maps and Möbius transformations.
Algebraic geometry
The relations between sides, diagonals and angles form algebraic varieties with interesting topological features.
Numerical methods
Modern computational methods enable solving complex cyclic quadrilateral problems and visualizing their properties.
Discrete geometry
Cyclic quadrilaterals on discrete grids and their applications in computer graphics and image processing.
Future perspectives
The cyclic quadrilateral remains relevant for future developments:
- Quantum geometry: Quantum systems with cyclic symmetries
- Machine learning: Geometric deep learning architectures
- Nanotechnology: Molecular machines with cyclic structures
- Virtual reality: Immersive environments with optimized geometric structures
- Biomechanics: Joint motion and biological constructions
- Sustainable design: Optimal structures for resource-efficient constructions
Summary
The cyclic quadrilateral stands as a timeless bridge between the ancient wisdom of Brahmagupta and Ptolemy and the modern demands of engineering and science. This inscribed geometric shape embodies mathematical elegance through its supplementary angles, the Brahmagupta formula and Ptolemy's theorem. As an optimum among quadrilaterals with given side lengths, it shows how nature unites efficiency and beauty. From gothic cathedrals to robot kinematics and quantum geometry, the cyclic quadrilateral remains a fundamental tool for understanding cyclic and optimal structures. It reminds us that ancient mathematical insights are timeless and retain their validity even in a high-tech future.
|
|
|
|