Calculate Rhombus Area (Rhombus)
Calculator and formulas for calculating the area of a rhombus
Rhombus Calculator
Rhombus
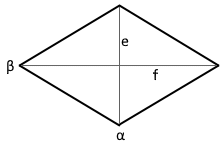
A rhombus has 4 sides of equal length and perpendicular diagonals. The area is calculated from the diagonals e and f.
Rhombus Visualization
The diagram shows a rhombus with diagonals e and f.
The diagonals are perpendicular to each other and bisect each other.
|
|
What is a Rhombus?
A rhombus is a special parallelogram with distinctive properties:
- 4 equal sides: All side lengths are identical
- Parallel sides: Opposite sides are parallel
- Equal angles: Opposite angles are equal
- Perpendicular diagonals: Diagonals meet at right angles
- Bisection: Diagonals bisect each other
- Area formula: A = (e × f) / 2
Properties of the Rhombus
The rhombus has characteristic geometric properties:
Diagonals
- Diagonals are perpendicular to each other
- Diagonals bisect each other
- Diagonals are axes of symmetry of the rhombus
- Divide the rhombus into 4 congruent right triangles
Sides and angles
- All four sides are equal in length
- Opposite angles are equal
- Adjacent angles are supplementary (sum to 180°)
- Sum of interior angles is 360°
Understanding the Area Calculation
The area calculation of the rhombus is based on its diagonals:
The basic idea
- Diagonal e: First diagonal of the rhombus
- Diagonal f: Second diagonal of the rhombus
- Formula: A = (e × f) / 2
- Diagonals are perpendicular!
Why does it work?
- The rhombus is divided into 4 right triangles
- Each triangle has area = (e/2 × f/2) / 2
- Total area = 4 × (e × f) / 8 = (e × f) / 2
- Equals half the rectangle spanned by the diagonals
Applications of Rhombi
Rhombi appear in many practical areas:
Jewelry & Design
- Diamonds and gemstones
- Jewelry design and ornaments
- Logo design and corporate identity
- Modern architectural elements
Architecture & Construction
- Tiles and flooring
- Window and facade design
- Roof structures
- Decorative building elements
Games & Entertainment
- Playing cards (diamond suit)
- Board games and puzzles
- Graphic design in video games
- Patterns and ornaments
Science & Technology
- Crystal structures in minerals
- Molecular geometry
- Optics and laser technology
- Mechanical engineering components
Formulas for the Rhombus
Area A
Half the product of the two diagonals
Perimeter P
From the diagonals using the Pythagorean theorem
Side length a
Compute side length from the diagonals
Angle α
Acute angle of the rhombus
Angle β
Obtuse angle of the rhombus
Angle relationship
Adjacent angles are supplementary
Important notes
- e, f: The two diagonals of the rhombus
- A: Area in square units
- P: Perimeter (4 × side length)
- α, β: The two distinct interior angles
- Diagonals are perpendicular to each other
- All sides are equal in length
Worked Example for a Rhombus
Given
Find: All properties of the rhombus
1. Compute area
Half the product of the diagonals
2. Compute side length
Pythagoras with half-diagonals
3. Compute perimeter
Four times the side length
4. Compute angles
Supplementary angles
5. Complete rhombus
A classic rhombus with the diagonal ratio 4:3
The Rhombus: Elegant Symmetry in Geometry and Design
The rhombus is one of the most fascinating geometric shapes, combining mathematical precision with aesthetic beauty. As a special parallelogram, it unites equal side lengths with the elegance of perpendicular diagonals.
Mathematical elegance and symmetry
The mathematical properties of the rhombus show remarkable elegance:
- Perfect equilateral shape: All four sides have exactly the same length
- Orthogonal diagonals: The diagonals are at right angles to each other
- Double symmetry: Both diagonals are lines of reflection
- Point symmetry: Symmetric about the intersection of the diagonals
- Simple area formula: A = (e × f) / 2 - elegant and practical
- Pythagorean relation: Side length follows from the Pythagorean theorem
The diagonals as the key to understanding
The diagonals of the rhombus are the key to all of its properties:
Orthogonality and bisection
The diagonals are perpendicular and bisect each other. This divides the rhombus into four congruent right triangles - the basis for all calculations.
Area calculation
The formula A = (e × f) / 2 equals half the rectangle spanned by the diagonals. Geometrically elegant and computationally simple.
Side-length relation
Each side is the hypotenuse of a right triangle with legs e/2 and f/2. Hence: a = √((e/2)² + (f/2)²).
Angle relations
The angles can be computed via arctangent: α = 2·arctan(f/e). Adjacent angles always add up to 180°.
Cultural and practical significance
The rhombus permeates culture and technology in many ways:
- Heraldry and symbolism: Diamond symbol for value and durability
- Jewelry design: Classic shape for gemstones and ornaments
- Architecture: Structural and aesthetic elements in buildings
- Playing cards: The diamond suit as a universal symbol
- Crystallography: Rhombic crystal systems in nature
- Graphic design: Modern logos and corporate identity
Relationships to other geometric shapes
The rhombus is related to other quadrilaterals in interesting ways:
Square as a special case
A square is a rhombus with equal diagonals (e = f) and 90° angles. It is the “perfect” rhombus with maximum symmetry.
Parallelogram as a superclass
Every rhombus is a parallelogram, but not every parallelogram is a rhombus. The rhombus adds the condition of equal side lengths.
Relation to kites
Kites also have perpendicular diagonals, but unequal side lengths. The rhombus is a special, symmetric kite.
Rectangle duality
While rectangles emphasize right angles, the rhombus emphasizes equal side lengths. Both are special parallelograms with complementary properties.
Modern applications and innovations
The rhombus continues to inspire modern developments:
- Nanotechnology: Rhombic lattice structures in materials science
- Computer graphics: Efficient algorithms for rhombic pixel structures
- Architecture: Modern facade design with rhombic elements
- Game development: Isometric projections and tile-based worlds
- Optics: Rhombic prisms for refraction and beam steering
Summary
The rhombus embodies geometric elegance by uniting equal side lengths and orthogonal diagonals. Its simple area formula A = (e × f) / 2 hides a rich mathematical structure ranging from the Pythagorean relation to trigonometric angle calculations. As a symbol of perfection and value, it permeates culture, art and technology. In a world of increasing geometric complexity, the rhombus remains a timeless example of how mathematical beauty and practical applicability go hand in hand.
|
|
|
|