Convert rectangle to square
Calculator for area-equal square-rectangle transformations
Square ⇄ Rectangle Converter
Area-equal transformation
Conversion between rectangle and square with identical area using geometric optimization.
Square ⇄ Rectangle comparison
Transformation properties
Principle: Same area A, different perimeters and proportions
Square and rectangle with equal area.
The square has the minimal perimeter.
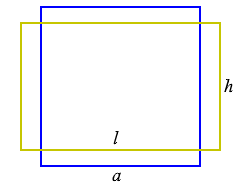
|
|
Square-Rectangle transformation: the art of area-preserving conversion
The transformation between square and rectangle with equal area demonstrates fundamental principles of geometry:
- Area equality: A□ = A▭ = constant
- Square-root relation: a = √(l × h)
- Perimeter optimization: Square has minimal perimeter
- Proportion change: From 1:1 to l:h ratio
- Isoperimetric problem: Optimal area-perimeter relation
- Geometric efficiency: Square as optimal shape
Geometric principles of area conversion
The mathematical relations between area-equal squares and rectangles:
Area preservation
- Square: A = a²
- Rectangle: A = l × h
- Equality: a² = l × h
- Transformation: a = √(l × h)
Perimeter differences
- Square: P□ = 4a = 4√(l × h)
- Rectangle: P▭ = 2(l + h)
- Minimal perimeter for the square
- Isoperimetric optimum
Mathematics of area transformation
The algebraic relations enable elegant conversions:
Square-root relations
- a = √A (from area)
- a = √(l × h) (from rectangle)
- h = A/l = a²/l (compute height)
- l = A/h = a²/h (compute length)
Optimization principles
- Minimal perimeter for given area
- Geometric vs. arithmetic mean
- Lagrange multipliers
- Foundations of calculus of variations
Applications of the square-rectangle transformation
Area conversions have many practical meanings:
Architecture & planning
- Floorplan optimization for equal area
- Energy-efficient building proportions
- Material efficiency for exterior walls
- Space planning and furnishing
Production & manufacturing
- Material cutting optimization
- Packaging design and efficiency
- Logistics and storage planning
- Production layout optimization
Digital & interface design
- Responsive layout design
- Screen optimization for various formats
- UI element proportions
- Print vs. digital format adjustments
Nature & environment
- Landscape design and planning
- Garden design for optimal area usage
- Biological habitat optimization
- Eco-system design and biodiversity
Formulas for Square ⇄ Rectangle transformation
Square side length a
Geometric mean of the rectangle sides
Rectangle dimensions
Inverse relations for rectangle sides
Area A
Area equality as fundamental principle
Perimeter relations
Different perimeters for the same area
Perimeter optimization
Square has minimal perimeter for given area
Geometric mean
Geometric ≤ arithmetic mean
Worked example for Square-Rectangle transformation
Given
Find: All parameters of the area-equal square and rectangle
1. Complete the rectangle
Height from area and length, then perimeter
2. Compute square
Side from area, then perimeter
3. Confirm transformation
Square-root relation and geometric mean confirmed
4. Complete transformation
Same area, square has 20% less perimeter!
The Square-Rectangle transformation: optimization in geometry
The transformation between square and rectangle for constant area embodies fundamental principles of geometric optimization. This seemingly simple conversion reveals deep mathematical truths about efficiency, the geometric mean and the famous isoperimetric problem. From antiquity to modern architecture this transformation shapes our understanding of optimal forms.
The isoperimetric problem and its solution
The Square-Rectangle transformation illustrates a special case of the isoperimetric problem:
- Perimeter minimization: For a given area the square has the smallest perimeter
- Geometric mean: a = √(l×h) - fundamental relation between dimensions
- AM-GM inequality: √(l×h) ≤ (l+h)/2 with equality only for l = h (square)
- Calculus of variations: Mathematical proof of the square's optimality
- Lagrange multipliers: Elegant optimization method for constraints
- Perimeter efficiency: Square is the most "economical" rectangular shape
Historical development and cultural meaning
The insight into square optimization has a long history:
Ancient mathematics
The ancient Greeks already recognized that the square minimizes the perimeter for a given area. Euclid treated related problems in his "Elements".
Medieval geometry
Islamic mathematicians developed algebraic methods for area conversion, influencing later Renaissance architecture.
Modern analysis
Euler and the Bernoullis formalized the calculus of variations, making the optimality of the square provable.
Contemporary application
Today architects and designers use these principles for energy-efficient buildings and material-optimized constructions.
Practical impacts in engineering and design
The Square-Rectangle transformation has far-reaching practical consequences:
- Energy-efficient architecture: Square floorplans minimize heat loss
- Material optimization: Less exterior-wall material for same interior area
- Production efficiency: Optimal cutting of rectangular materials
- Logistics optimization: Best space utilization in square containers
- Urban planning: Square city blocks for optimal infrastructure
- Display technology: Square pixels for efficient screen layouts
Mathematical depth and connections
The transformation reveals deep mathematical connections:
Geometric means
The geometric mean √(l×h) is always less than or equal to the arithmetic mean (l+h)/2. This inequality explains the perimeter efficiency of the square.
Optimization theory
The square transformation is a prime example of constrained optimization. Lagrange multipliers lead elegantly to the solution.
Differential geometry
The curvature of the "iso-area curves" in the (l,h) parameter space geometrically explains why the square is optimal.
Functional analysis
The problem can be formulated as minimizing a functional in a Hilbert space - a gateway to modern analysis.
Future perspectives and modern applications
The principles of the Square-Rectangle transformation remain highly relevant:
- Sustainable architecture: Climate-neutral buildings use optimal floor proportions
- AI-optimized layouts: Machine learning finds optimal room divisions
- 3D-printing: Material-efficient structures via geometric optimization
- Nano-engineering: Optimal shapes for molecular machines
- Space habitats: Space stations use optimal geometries for living space
- Virtual reality: Optimized virtual rooms for immersive experiences
Summary
The Square-Rectangle transformation embodies the essence of geometric optimization. This elegant mathematical relation - a = √(l×h) - connects the geometric mean with the isoperimetric problem and shows how the square achieves minimal perimeter for a given area. From ancient Greek insights through modern calculus of variations to contemporary applications in sustainable architecture and AI-optimized design, this fundamental transformation remains a cornerstone of efficient design. It reminds us that within the apparent simplicity of the square lies a deep mathematical truth - the perfect balance between form and function, between aesthetics and efficiency.
|
|
|
|