Calculate general quadrilateral

Calculator for arbitrary quadrilaterals without special symmetries

General quadrilateral calculator

General quadrilateral

A general quadrilateral is the most versatile quadrilateral form with arbitrary side lengths and angles.

Enter three sides and two connecting angles
Input required: 3 side lengths (a, b, c) + 2 angles (β, γ) to determine uniquely
First side
Second side
Third side
Angle between sides a and b
Angle between sides b and c
General quadrilateral results
Side length d:
Diagonal e:
Diagonal f:
Area A:
Perimeter U:
Angle α:
Angle δ:
Angle sum:
α + β + γ + δ = 360°

General quadrilateral

General quadrilateral properties

Versatile: No special symmetries, arbitrary sides and angles

4 arbitrary sides 4 arbitrary angles Bretschneider formula

General quadrilateral without special symmetry.
Arbitrary side lengths and angles possible.

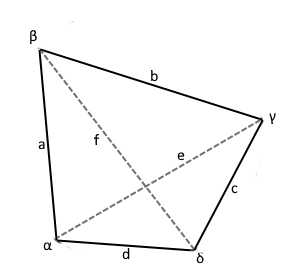
General quadrilateral

The general quadrilateral: versatility without constraints

The general quadrilateral is the most comprehensive form of quadrilateral geometry:

  • Arbitrary shape: No special symmetries or properties
  • Variable sides: All four side lengths can differ
  • Flexible angles: All four angles may vary
  • Complex computation: Requires Bretschneider formula
  • Unique determination: 5 parameters (3 sides + 2 angles)
  • Universal application: Basis for all quadrilateral types

Geometric properties of general quadrilaterals

The mathematical properties are characterized by generality:

Angle properties
  • Angle sum: α + β + γ + δ = 360°
  • No special angle relations
  • All angles between 0° and 180° possible
  • Determination via law of cosines and geometry
Sides and diagonals
  • All four sides may differ
  • Diagonals computable with law of cosines
  • No special diagonal properties
  • Complex relationships between all parameters

Mathematics of general quadrilateral calculation

The mathematical treatment uses advanced methods:

Bretschneider formula
  • Generalization of Brahmagupta's formula
  • Accounts for arbitrary angles
  • Complex expression with trigonometric terms
  • Fundamental area computation
Stepwise calculation
  • Diagonals via law of cosines
  • Fourth side via auxiliary triangles
  • Remaining angles via law of cosines
  • Area via Bretschneider formula

Applications of general quadrilaterals

General quadrilaterals are omnipresent in the real world:

Surveying & geography
  • Property surveying and cadastral mapping
  • Cartography and land surveying
  • GPS-based area determination
  • Satellite image analysis
Architecture & construction
  • Irregular building footprints
  • Roof constructions and gables
  • Landscape architecture
  • Urban planning and parceling
Computer graphics & CAD
  • 3D modeling and mesh generation
  • CAD software for technical drawing
  • Game development and level design
  • Finite element methods
Engineering
  • Mechanical components
  • Structural analysis and statics
  • Material cutting optimization
  • Robotics and motion planning

Formulas for the general quadrilateral

Diagonal e
\[e = \sqrt{a^2 + b^2 - 2ab \cos(\beta)}\]

Law of cosines for diagonal e from sides a, b

Diagonal f
\[f = \sqrt{b^2 + c^2 - 2bc \cos(\gamma)}\]

Law of cosines for diagonal f from sides b, c

Side length d
\[d = \sqrt{c^2 + e^2 - 2ce \cos(\gamma_2)}\]

With auxiliary angle γ₂ = γ - γ₁

Perimeter U
\[U = a + b + c + d\]

Sum of all four side lengths

Angle α
\[\alpha = \arccos\left(\frac{a^2 + d^2 - f^2}{2ad}\right)\]

Law of cosines applied backward

Angle δ
\[\delta = 360° - \alpha - \beta - \gamma\]

Angle sum in a quadrilateral

Bretschneider area formula
\[A = \sqrt{(s-a)(s-b)(s-c)(s-d) - abcd \cos^2\left(\frac{\alpha + \gamma}{2}\right)}\] \[s = \frac{a + b + c + d}{2}\]

Generalization of Brahmagupta's formula for arbitrary quadrilaterals

Worked example for a general quadrilateral

Given
Side a = 7 Side b = 5 Side c = 6 Angle β = 80° Angle γ = 70°

Find: All missing parameters of the general quadrilateral

1. Compute diagonals
\[e = \sqrt{7^2 + 5^2 - 2 \times 7 \times 5 \times \cos(80°)} = 6.87\] \[f = \sqrt{5^2 + 6^2 - 2 \times 5 \times 6 \times \cos(70°)} = 6.04\]

Law of cosines for both diagonals

2. Fourth side d
\[\gamma_1 = \arccos\left(\frac{5^2 + 6.87^2 - 7^2}{2 \times 5 \times 6.87}\right) = 52.3°\] \[d = \sqrt{6^2 + 6.87^2 - 2 \times 6 \times 6.87 \times \cos(17.7°)} = 2.87\]

With auxiliary angle γ₂ = 70° - 52.3° = 17.7°

3. Missing angles
α = arccos((49 + 8.24 - 36.48)/40.18) = 58.7°
δ = 360° - 58.7° - 80° - 70° = 151.3°

Law of cosines and angle sum

4. Complete general quadrilateral
Sides: a=7, b=5, c=6, d=2.87 Perimeter U = 20.87 Diagonals: e=6.87, f=6.04
Angles: α=58.7°, β=80°, γ=70°, δ=151.3° Area A ≈ 26.8 (Bretschneider)

Fully determined general quadrilateral with all parameters!

The general quadrilateral: universal geometry without bounds

The general quadrilateral serves as the most comprehensive form of quadrilateral geometry at the center of modern mathematical applications. Without special symmetries or constraints it embodies the pure versatility of geometric forms and applies wherever the real world shows irregular yet mathematically describable structures. From land surveying to computer graphics and structural analysis it forms the basis for understanding complex geometric relationships.

Mathematical universality

The general quadrilateral demonstrates fundamental geometric principles:

  • Bretschneider formula: Generalization of Brahmagupta's formula for arbitrary quadrilaterals
  • Law of cosines application: Systematic computation of diagonals and missing sides
  • Angle sum 360°: Fundamental property of all planar quadrilaterals
  • Unique determination: Five parameters (3 sides + 2 angles) define everything
  • Trigonometric completeness: All relations via sine and law of cosines
  • Geometric flexibility: Basis for all special quadrilateral types

Practical relevance in the real world

General quadrilaterals are omnipresent in practical applications:

Surveying and cartography

Property boundaries rarely follow ideal geometric shapes. The general quadrilateral enables precise area calculations for cadastre and land registry.

Architecture and construction

Modern architecture deliberately uses irregular shapes. General quadrilaterals allow mathematical description of innovative building geometries.

Computer graphics and CAD

3D modeling is based on polygon meshes of general quadrilaterals. Any complex surface can be approximated by quadrilateral tessellation.

Engineering

Finite element methods use general quadrilaterals as base elements for structural analyses, flow simulations and material calculations.

Mathematical challenges and solutions

Dealing with general quadrilaterals requires advanced mathematical methods:

  • Bretschneider formula (1842): Historical extension of Brahmagupta's formula
  • Complex trigonometry: Systematic use of law of cosines and auxiliary angles
  • Numerical stability: Precise computation even for extreme side ratios
  • Algorithmic efficiency: Optimized computation sequence for CAD systems
  • Error analysis: Handling rounding errors and numerical instabilities
  • Geometric validation: Checking constructability and physical plausibility

Future perspectives and modern developments

The general quadrilateral remains relevant for future technologies:

Artificial intelligence

Machine learning algorithms for geometry recognition and classification rely on general quadrilateral properties. Computer vision uses these for object detection.

Digital twins

Accurate 3D models of real objects require exact geometry computations. General quadrilaterals are fundamental for digital representations.

Robotics and automation

Robot navigation in unstructured environments requires understanding arbitrary geometric shapes and their mathematical description.

Sustainable design

Optimized material usage requires precise area computations of irregular shapes. General quadrilaterals minimize waste and offcuts.

Summary

The general quadrilateral stands as the mathematical foundation for describing arbitrary four-sided shapes without special constraints. Its universal applicability — from the Bretschneider formula through trigonometric relations to modern CAD systems — makes it an indispensable tool of applied mathematics. In a world of increasingly complex geometries, from architecture and computer graphics to AI-driven systems, understanding general quadrilaterals is fundamental for engineers, architects, programmers and scientists. It reminds us that mathematical elegance is not only found in perfect symmetries, but also in the ability to precisely describe and understand the irregular.

Is this page helpful?            
Thank you for your feedback!

Sorry about that

How can we improve it?

Square • Rectangle • Golden Rectangle • Rectangle to Square • Rhombus, given varios parameter • Rhombus , given diagonal e, f • Parallelogram, given 2 sides and angle • Parallelogram area, given side and height • Trapezoid • Cyclic Quadrilateral • General Quadrilateral • Concave Quadrilateral • Arrowhead Quadrilateral • Crossed Square • Frame • Kite, given 2 diagonal and distance • Kite Area, given 2 diagonal • Half Square Kite • Right Kite"