Right Kite Calculator

Calculator and formulas for calculating the properties of a right kite (right-angled deltoid)

Right Kite Calculator

The Right Kite

A right kite is a special kite with two opposite right angles between the short and long sides.

Enter Side Lengths
Input: Enter the lengths of sides a and b
Short side length
Long side length
Right Kite Properties

Key Feature: Two opposite right angles (90°)

Side a Side b ∠B = ∠D = 90°
Right Kite Results
Perimeter P:
Area A:
Diagonal e:
Diagonal f:
Angle α:
Angle γ:
Incircle radius ri:
Outer radius rc:
The right kite has two opposite right angles (∠B = ∠D = 90°)

Right Kite Structure

A right kite has two opposite right angles.
The diagonals are perpendicular.

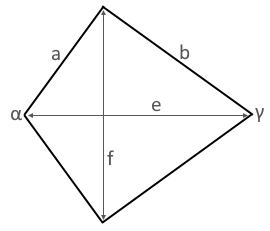
Right Kite Diagram

● Edge a (short side) ● Edge b (long side) ● Right angles at B and D


What is a Right Kite?

A right kite (or right-angled deltoid) is a special type of kite with unique geometric properties:

  • Definition: Kite with two opposite right angles (90°) between short and long sides
  • Perpendicular diagonals: Diagonals e and f meet at right angles
  • Symmetry axis: Diagonal e (from A to C) is the axis of symmetry
  • Isosceles triangles: Diagonal f divides the kite into two isosceles triangles
  • Equal opposite angles: Angles at B and D are both 90°
  • Cyclic quadrilateral: Can be inscribed in a circle

Geometric Properties

The right kite possesses special geometric properties:

Side and Angle Properties
  • Two opposite right angles: ∠B = ∠D = 90°
  • Adjacent equal sides: AB = AD = a and CB = CD = b
  • Four vertices: Points A, B, C, D form the kite
  • Complementary angles: α + γ = 180°
Diagonal Properties
  • Perpendicular: Diagonals e and f intersect at 90°
  • Symmetry diagonal e: Axis of symmetry of the kite
  • Diagonal e: e = √(a² + b²) (Pythagorean theorem)
  • Simple area: A = a · b (product of sides)

Mathematical Relationships

The right kite follows elegant mathematical formulas:

Area Calculation
A = a · b

The area is simply the product of the two side lengths. This elegant formula results from the two right angles.

Perimeter Calculation
P = 2(a + b)

The perimeter is twice the sum of the two different side lengths.

Formulas for the Right Kite

Area A
\[A = a \cdot b\]

Simple product of the two side lengths

Perimeter P
\[P = 2 \cdot (a + b)\]

Sum of all four sides

Diagonal e
\[e = \sqrt{a^2 + b^2}\]

Using Pythagorean theorem (hypotenuse)

Diagonal f
\[f = \frac{2ab}{e} = \frac{2ab}{\sqrt{a^2 + b^2}}\]

Cross diagonal formula

Angle α
\[\alpha = \arccos\left(\frac{a^2 + e^2 - b^2}{2ae}\right)\]

Angle at vertex A using law of cosines

Angle γ
\[\gamma = 180° - \alpha\]

Complementary angle at vertex C

Incircle radius ri
\[r_i = \frac{ab}{a + b}\]

Radius of inscribed circle

Circumcircle radius rc
\[r_c = \frac{e}{2} = \frac{\sqrt{a^2 + b^2}}{2}\]

Radius of circumscribed circle

Right Angles
\[\angle B = \angle D = 90°\]

Defining characteristic

Perpendicular Diagonals
\[e \perp f\]

Diagonals intersect at 90°

Calculation Example

Given
Edge a = 3 Edge b = 5

Find: All properties of the right kite

1. Calculate Area
\[A = a \cdot b\] \[A = 3 \times 5\] \[A = 15\]

Simple product of sides

2. Calculate Perimeter
\[P = 2(a + b)\] \[P = 2(3 + 5)\] \[P = 2 \times 8 = 16\]

Total perimeter

3. Calculate Diagonal e
\[e = \sqrt{a^2 + b^2}\] \[e = \sqrt{3^2 + 5^2}\] \[e = \sqrt{9 + 25} = \sqrt{34} \approx 5.83\]

Using Pythagorean theorem

4. Calculate Diagonal f
\[f = \frac{2ab}{e}\] \[f = \frac{2 \times 3 \times 5}{5.83}\] \[f = \frac{30}{5.83} \approx 5.15\]

Cross diagonal

5. Calculate Angle α
\[\alpha = \arccos\left(\frac{3^2 + 5.83^2 - 5^2}{2 \times 3 \times 5.83}\right)\] \[\alpha = \arccos\left(\frac{9 + 34 - 25}{35}\right)\] \[\alpha \approx 59.0°\]

Angle at vertex A

6. Calculate Angle γ
\[\gamma = 180° - \alpha\] \[\gamma = 180° - 59.0°\] \[\gamma = 121.0°\]

Complementary angle

7. Incircle Radius
\[r_i = \frac{ab}{a + b}\] \[r_i = \frac{3 \times 5}{3 + 5}\] \[r_i = \frac{15}{8} = 1.88\]

Inscribed circle radius

8. Circumcircle Radius
\[r_c = \frac{e}{2}\] \[r_c = \frac{5.83}{2}\] \[r_c = 2.92\]

Circumscribed circle radius

9. Summary of Results
P = 16 A = 15
e = 5.83 f = 5.15
α ≈ 59° γ ≈ 121°
ri = 1.88 rc = 2.92

Complete properties of a right kite with sides a=3 and b=5

Applications of Right Kites

Right kite shapes appear in various practical applications:

Architecture & Construction
  • Roof designs and gable structures
  • Window and door frames
  • Decorative architectural elements
  • Floor plan layouts
Art & Design
  • Geometric artwork and patterns
  • Tile and mosaic designs
  • Quilting and textile patterns
  • Logo and graphic design
Mathematics Education
  • Teaching Pythagorean theorem
  • Demonstrating right angles
  • Exploring quadrilateral properties
  • Circle geometry applications
Engineering
  • Structural bracing systems
  • Mechanical linkages
  • Frame design components
  • Support structures

The Right Kite: Elegance Through Right Angles

The right kite (right-angled deltoid) is a remarkable special case among kite quadrilaterals. Its defining characteristic — two opposite right angles between the short and long sides — creates exceptionally elegant geometric relationships and simple mathematical formulas.

Definition and Fundamental Properties

The right kite is characterized by several key features:

  • Two opposite right angles: ∠B = ∠D = 90° (at opposite vertices)
  • Kite properties retained: Two pairs of adjacent equal sides (AB = AD = a, CB = CD = b)
  • Perpendicular diagonals: Diagonals e and f meet at right angles
  • Symmetry axis: Diagonal e serves as the axis of symmetry
  • Cyclic quadrilateral: Can be inscribed in a circle (circumcircle)
  • Tangential quadrilateral: Has an inscribed circle (incircle)

The Elegant Area Formula

One of the most beautiful properties of the right kite:

Why A = a · b?

The two opposite right angles at B and D allow the kite to be perfectly inscribed in a rectangle with sides a and b. The kite's area equals exactly the area of this rectangle, leading to the remarkably simple formula A = a · b.

Geometric Insight

If you draw the right kite inside a rectangle with dimensions a × b, the kite perfectly fills the entire rectangle. This is unique to the right kite and makes area calculations trivial.

Connection to Right Triangles

The diagonal e divides the right kite into two congruent right triangles with legs a and b. Using the Pythagorean theorem, e = √(a² + b²), showing the deep connection to fundamental geometry.

Circle Properties

Because opposite angles sum to 180° (90° + 90° = 180°, α + γ = 180°), the right kite can be inscribed in a circle. The circumradius is rc = e/2, making the diagonal e the diameter of the circumcircle.

Mathematical Elegance

The right kite demonstrates several beautiful mathematical principles:

Pythagorean Relationships

The right angles create natural right triangles within the kite. The diagonal e, connecting the non-right-angle vertices, acts as the hypotenuse: e² = a² + b². This makes the right kite an ideal teaching tool for the Pythagorean theorem.

Symmetry and Calculation

The axis of symmetry along diagonal e simplifies all calculations. Every property on one side of this axis is mirrored on the other, reducing computational complexity and providing elegant verification methods.

Inscribed and Circumscribed Circles

The right kite is both tangential (has an incircle) and cyclic (has a circumcircle). The incircle radius ri = ab/(a+b) and circumcircle radius rc = e/2 provide beautiful relationships between the kite's dimensions and its associated circles.

Trigonometric Relations

The angles α and γ are complementary (α + γ = 180°), creating elegant trigonometric relationships. For example, sin(α) = sin(γ) and cos(α) = -cos(γ), which simplify many calculations.

Related Geometric Shapes

The right kite connects to other important geometric figures:

Square (When a = b)

When the two side lengths become equal (a = b), the right kite becomes a square. All four angles become 90°, and both diagonals become equal, demonstrating the square as a special limiting case.

General Kite

The right kite is a special case of the general kite where two opposite angles happen to be 90°. All general kite properties apply, plus the additional constraints from the right angles create simpler formulas.

Rectangle Connection

Unlike other kites, the right kite perfectly fits a rectangle with dimensions a × b. This unique property makes it a bridge between kites and rectangles in geometric classification.

Right Triangle Pair

The diagonal e divides the right kite into two congruent right triangles, each with legs a and b and hypotenuse e. This decomposition provides multiple solution approaches.

Summary

The right kite exemplifies how adding a geometric constraint (two opposite right angles) to an already special shape (the kite) creates remarkably simple and elegant mathematical relationships. The formula A = a · b rivals the rectangle in simplicity, while the Pythagorean relationship e² = a² + b² connects it to fundamental geometry. From architectural applications to mathematical education, this geometric figure demonstrates that beauty and utility often arise from simple, well-chosen constraints. The right kite reminds us that geometry at its best combines visual elegance with mathematical clarity.

Is this page helpful?            
Thank you for your feedback!

Sorry about that

How can we improve it?

Square • Rectangle • Golden Rectangle • Rectangle to Square • Rhombus, given varios parameter • Rhombus , given diagonal e, f • Parallelogram, given 2 sides and angle • Parallelogram area, given side and height • Trapezoid • Cyclic Quadrilateral • General Quadrilateral • Concave Quadrilateral • Arrowhead Quadrilateral • Crossed Square • Frame • Kite, given 2 diagonal and distance • Kite Area, given 2 diagonal • Half Square Kite • Right Kite"