Concave Quadrilateral Calculator

Calculator and formulas for concave quadrilaterals

Concave Quadrilateral Calculator

Concave Quadrilateral

A concave quadrilateral has at least one inward-pointing vertex and complex diagonal behaviour.

Enter sides and angles
First side
Second side
Third side
Angle in degrees
Angle in degrees
Concave quadrilateral results
Side d:
Diagonal e:
Diagonal f:
Area A:
Perimeter U:
Angles α, δ: ,

Concave Quadrilateral

Concave properties

Key feature: At least one interior angle > 180°, complex diagonals

4 sides a,b,c,d 4 angles α,β,γ,δ Diagonals e,f

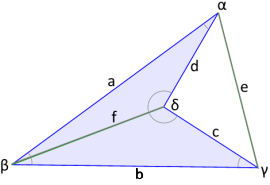
The concave quadrilateral with an inward-pointing vertex.
One diagonal may lie outside the figure.

Concave Quadrilateral

The concave quadrilateral: inward-pointing geometry

A concave quadrilateral differs fundamentally from convex quadrilaterals:

  • Concave: "curved inward" (latin: concavus)
  • Inward vertex: At least one angle > 180°
  • Diagonal issue: A diagonal may lie outside the figure
  • Complex computation: Requires triangle decomposition
  • Applications: Architecture, design, engineering
  • Special case: Not all standard formulas apply

Geometric properties of concave quadrilaterals

The geometry of concave quadrilaterals brings special challenges:

Angle properties
  • Angle sum: α + β + γ + δ = 360°
  • At least one interior angle > 180°
  • Reflex angles create concavity
  • Complex angle calculations needed
Diagonal behaviour
  • A diagonal may lie outside the figure
  • Different calculation methods apply
  • Law of cosines for diagonals e and f
  • Auxiliary-angle preparation for side d

Computation methodology for concave quadrilaterals

The mathematical treatment of concave quadrilaterals requires special approaches:

Triangle decomposition
  • Split into two subtriangles
  • Law of cosines for diagonal calculation
  • Auxiliary angle β₁ for complex geometry
  • Heron's formula for subareas
Stepwise calculation
  • 1. Compute diagonals e and f
  • 2. Determine auxiliary angle β₁
  • 3. Compute missing side d
  • 4. Determine remaining angles α and δ

Applications of concave quadrilaterals

Concave quadrilaterals have many practical applications:

Architecture & construction
  • Modern building floorplans
  • Roof constructions with recesses
  • Courtyards and building niches
  • Façade designs with setbacks
Engineering & design
  • Mechanical components
  • PCB layout designs
  • Automotive body parts
  • Furniture design and functionality
Gaming & simulation
  • Level design in video games
  • Polygon meshes in 3D modelling
  • Collision-detection algorithms
  • Terrain generation and landscapes
Art & media
  • Graphic design and logo development
  • Photographic composition
  • Digital art and animation
  • UI/UX design for apps

Formulas for the concave quadrilateral

Diagonal e
\[e = \sqrt{a^2 + b^2 - 2 \cdot a \cdot b \cdot \cos(\beta)}\]

Law of cosines for diagonal e

Diagonal f
\[f = \sqrt{b^2 + c^2 - 2 \cdot b \cdot c \cdot \cos(\gamma)}\]

Law of cosines for diagonal f

Auxiliary angle β₁
\[\beta_1 = \beta - \arccos\left(\frac{b^2 + f^2 - c^2}{2 \cdot b \cdot f}\right)\]

Used for computing side d

Side d
\[d = \sqrt{a^2 + f^2 - 2 \cdot a \cdot f \cdot \cos(\beta_1)}\]

Fourth side using auxiliary angle

Angle α
\[\alpha = \arccos\left(\frac{a^2 + d^2 - f^2}{2 \cdot a \cdot d}\right)\]

Back-calculated using the law of cosines

Angle δ
\[\delta = 360° - \alpha - \beta - \gamma\]

Angle sum in the quadrilateral

Perimeter U
\[U = a + b + c + d\]

Sum of all four sides

Area A (Heron)
\[A = \sqrt{s_1(s_1-a)(s_1-d)(s_1-f)} + \sqrt{s_2(s_2-b)(s_2-c)(s_2-f)}\]
with \(s_1 = \frac{a+d+f}{2}\), \(s_2 = \frac{b+c+f}{2}\)

Heron's formula for both subtriangles

Worked example for a concave quadrilateral

Given
Side a = 7 Side b = 5 Side c = 3 Angle β = 50° Angle γ = 30°

Find: All missing parameters of the concave quadrilateral

1. Compute diagonals
\[e = \sqrt{7^2 + 5^2 - 2 \times 7 \times 5 \times \cos(50°)} = 5.24\] \[f = \sqrt{5^2 + 3^2 - 2 \times 5 \times 3 \times \cos(30°)} = 3.21\]

Law of cosines for both diagonals

2. Auxiliary angle β₁
\[\beta_1 = 50° - \arccos\left(\frac{5^2 + 3.21^2 - 3^2}{2 \times 5 \times 3.21}\right)\] \[\beta_1 \approx 27.8°\]

Needed to compute side d

3. Missing side and angle
d = √(49 + 10.30 - 31.84) = 5.25
α = arccos((49 + 27.56 - 10.30)/73.5) = 64.2°

Side d and angle α computed from values

4. Complete concave quadrilateral
Sides: a=7, b=5, c=3, d=5.25 Angles: α=64.2°, β=50°, γ=30°, δ=215.8°
Perimeter U = 20.25 Area A ≈ 12.8 Diagonals: e=5.24, f=3.21

Complete concave quadrilateral — note reflex angle δ > 180°!

The concave quadrilateral: challenges of non-convex geometry

The concave quadrilateral represents one of the more complex quadrilateral shapes. With at least one inward-pointing vertex and the characteristic property that a diagonal may lie outside the figure, it requires specialized mathematical treatment methods and nevertheless finds many applications in engineering, architecture and design.

Special properties of concave geometry

Concave quadrilaterals differ fundamentally from their convex counterparts:

  • Reflex angles: At least one interior angle > 180° creates the characteristic indentation
  • Diagonal issue: One of the diagonals may lie outside the figure
  • Complex area computation: Decomposition into subtriangles required
  • Non-trivial construction: Standard quadrilateral formulas do not apply
  • Visibility issues: Not all points are visible from all others
  • Orientation matters: Clockwise vs counter-clockwise affects computations

Mathematical solution strategies

Calculating concave quadrilaterals requires clever mathematical approaches:

Triangle decomposition

The concave quadrilateral is split along a diagonal into two triangles, for which known formulas (law of cosines, Heron) can be applied.

Stepwise calculation

First compute the diagonals using the law of cosines, then determine the auxiliary angles, compute the missing side and finally all angles.

Angle management

Handling angles > 180° requires special care with trigonometric calculations and correct interpretation of inverse functions.

Validation is important

Results must be validated carefully because not all geometrically plausible quadrilaterals are solvable numerically.

Practical applications

Despite being more complex to calculate, concave quadrilaterals have important practical applications:

  • Architecture: Modern buildings with recesses, courtyards and complex floorplans
  • Industrial design: Mechanical parts with functional cutouts and niches
  • Computer graphics: Polygon rendering, collision detection and spatial algorithms
  • Urban planning: Building blocks with courtyards and traffic cutouts
  • Furniture design: Ergonomic shapes and functional recesses
  • Electronics: PCB layouts with cutouts for components

Challenges and limits

Working with concave quadrilaterals introduces special challenges:

Computational complexity

Higher mathematical complexity demands more steps and greater care with numerical accuracy.

Construction limits

Not every combination of sides and angles yields a constructible concave quadrilateral - geometric consistency is crucial.

Software implementation

CAD software and computation programs must implement special algorithms for concave polygons.

Visualization issues

Rendering and understanding concave shapes is harder because they can contradict intuitive expectations.

Concave geometry in the digital world

In the digital era concave quadrilaterals gain new relevance:

  • Game development: Level design with complex non-convex spaces
  • 3D modelling: Basis for more complex concave 3D bodies
  • Robotics: Path planning around concave obstacles
  • Computer vision: Object recognition and shape analysis
  • Finite elements: Discretization of complex geometries in simulation
  • Artificial intelligence: Spatial reasoning and geometry understanding
Summary

The concave quadrilateral is an important example of how mathematical complexity and practical application go hand in hand. Although the computation is more demanding than for convex quadrilaterals, concave geometry opens up new possibilities in design, architecture and engineering. The characteristic indentation with a reflex angle > 180° and the exterior diagonal requires special mathematical methods but offers functional and aesthetic advantages. In our increasingly digital world, where complex geometries gain importance in computer graphics, robotics and AI, understanding concave quadrilaterals remains a valuable building block for mastering non-convex geometric structures.

Square • Rectangle • Golden Rectangle • Rectangle to Square • Rhombus, given varios parameter • Rhombus , given diagonal e, f • Parallelogram, given 2 sides and angle • Parallelogram area, given side and height • Trapezoid • Cyclic Quadrilateral • General Quadrilateral • Concave Quadrilateral • Arrowhead Quadrilateral • Crossed Square • Frame • Kite, given 2 diagonal and distance • Kite Area, given 2 diagonal • Half Square Kite • Right Kite"