Quadratische Pyramide Rechner
Rechner und Formeln zur Berechnung der Parameter einer quadratischen Pyramide
Pyramide Rechner
Die quadratische Pyramide
Diese Funktion berechnet verschiedene Parameter einer geraden, quadratischen Pyramide. Zur Berechnung geben Sie die Seitenlänge und die Höhe ein.
Quadratische Pyramide Eigenschaften
Die klassische Pyramide: Quadratische Basis mit vier dreieckigen Seitenflächen
Pyramide Struktur
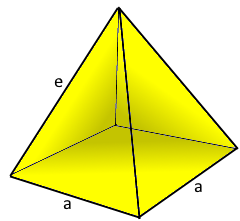
Die klassische quadratische Pyramide.
Symbol für Stabilität und Beständigkeit.
|
|
Was ist eine quadratische Pyramide?
Die quadratische Pyramide ist eine der wichtigsten geometrischen Formen:
- Definition: Polyeder mit quadratischer Basis und vier dreieckigen Seitenflächen
- Klassifizierung: Gerade Pyramide bei senkrechter Spitze über dem Zentrum
- Flächen: 1 quadratische Basis + 4 dreieckige Seitenflächen
- Ecken: 5 Ecken (4 Basis + 1 Spitze)
- Kanten: 8 Kanten (4 Basis + 4 seitlich)
- Bedeutung: Symbol für Stabilität und Ewigkeit
Geometrische Eigenschaften der Pyramide
Die quadratische Pyramide zeigt bemerkenswerte geometrische Eigenschaften:
Grundparameter
- Flächen: 5 (1 Quadrat + 4 Dreiecke)
- Ecken: 5 (4 Basis + 1 Spitze)
- Kanten: 8 (4 Basis + 4 seitlich)
- Euler-Charakteristik: V - E + F = 5 - 8 + 5 = 2
Besondere Eigenschaften
- Stabilität: Äußerst stabile Konstruktion
- Symmetrie: Vierfache Rotationssymmetrie
- Architektur: Häufig in Bauwerken verwendet
- Konvex: Alle Ecken ragen nach außen
Mathematische Beziehungen
Die quadratische Pyramide folgt klaren mathematischen Gesetzen:
Volumen-Formel
Ein Drittel der Grundfläche mal Höhe. Einfach und elegant.
Oberflächen-Formel
Grundfläche plus vier Dreiecksflächen. Pythagoras in Aktion.
Anwendungen der Pyramide
Quadratische Pyramiden finden Anwendung in verschiedenen Bereichen:
Architektur & Bauwesen
- Monumentale Bauwerke (Pyramiden von Gizeh)
- Moderne Gebäudespitzen
- Dachkonstruktionen
- Dekorative Elemente
Wissenschaft & Technik
- Kristallstrukturen
- Optische Prismen
- Strukturelle Analyse
- Materialprüfung
Bildung & Lehre
- Geometrie-Unterricht
- 3D-Geometrie-Studien
- Volumenberechnungen
- Pythagoras-Anwendungen
Kunst & Design
- Skulpturen
- Moderne Kunstwerke
- Produktdesign
- Architektonische Details
Formeln zur quadratischen Pyramide
Die folgenden Formeln beziehen sich auf die Berechnung einer geraden viereckigen Pyramide:
| Symbol | Parameter | Formel |
|---|---|---|
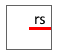 |
Radius zur Seite | \(\displaystyle r_s=\frac{a}{2}\) |
 |
Radius zur Ecke | \(\displaystyle r_v=\sqrt{({r_s}^2+{r_s}^2)} = \frac{a\sqrt{2}}{2}\) |
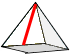 |
Mantelhöhe | \(\displaystyle s=\sqrt{h^2+{r_s}^2} = \sqrt{h^2+\frac{a^2}{4}}\) |
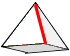 |
Kantenlänge | \(\displaystyle e=\sqrt{s^2+\frac{a^2}{4}}\) |
 |
Fläche einer Seite | \(\displaystyle A_S=\frac{s \cdot a}{2}\) |
 |
Mantelfläche | \(\displaystyle A_L=\frac{s \cdot P}{2} = 2 \cdot a \cdot \sqrt{h^2+\frac{a^2}{4}}\) |
 |
Grundfläche | \(\displaystyle A=a^2\) |
 |
Oberfläche | \(\displaystyle S=A+A_L = a^2 + 2a\sqrt{h^2+\frac{a^2}{4}}\) |
 |
Umfang der Basis | \(\displaystyle P=4 \cdot a\) |
 |
Volumen | \(\displaystyle V=\frac{A \cdot h}{3} = \frac{a^2 \cdot h}{3}\) |
 |
Höhe | \(\displaystyle h=\frac{3 \cdot V}{A} = \sqrt{s^2-{r_s}^2}\) |
Berechnungsbeispiel für eine quadratische Pyramide
Gegeben
Gesucht: Alle Eigenschaften der quadratischen Pyramide
1. Grundfläche und Umfang
Grundfläche:
\[A = a^2 = 10^2 = 100\]Umfang:
\[P = 4 \cdot a = 4 \cdot 10 = 40\]Grundfläche: 100 Flächeneinheiten, Umfang: 40 Längeneinheiten
2. Radien-Berechnung
Radius zur Seite:
\[r_s = \frac{a}{2} = \frac{10}{2} = 5\]Radius zur Ecke:
\[r_v = \frac{a\sqrt{2}}{2} = \frac{10\sqrt{2}}{2} ≈ 7.07\]Radius zur Seite: 5, Radius zur Ecke: 7.07
3. Höhen-Berechnungen
Mantelhöhe:
\[s = \sqrt{h^2+r_s^2} = \sqrt{8^2+5^2} = \sqrt{64+25} = \sqrt{89} ≈ 9.43\]Kantenhöhe:
\[e = \sqrt{h^2+r_v^2} = \sqrt{8^2+7.07^2} ≈ 10.77\]Mantelhöhe: 9.43, Kantenhöhe: 10.77
4. Flächen-Berechnungen
Seitenfläche (eine):
\[A_S = \frac{s \cdot a}{2} = \frac{9.43 \cdot 10}{2} ≈ 47.15\]Mantelfläche (gesamt):
\[A_L = 4 \cdot A_S = 4 \cdot 47.15 ≈ 188.6\]Eine Seitenfläche: 47.15, Mantelfläche: 188.6
5. Volumen und Oberfläche
Volumen:
\[V = \frac{A \cdot h}{3} = \frac{100 \cdot 8}{3} ≈ 266.67\]Oberfläche:
\[S = A + A_L = 100 + 188.6 = 288.6\]Volumen: 266.67, Oberfläche: 288.6
6. Die perfekte Pyramide
Die quadratische Pyramide mit klassischen Proportionen
Die quadratische Pyramide: Symbol für Beständigkeit
Die quadratische Pyramide ist eine der bedeutendsten geometrischen Formen in der Geschichte der Menschheit. Von den monumentalen Pyramiden von Gizeh bis zu modernen architektonischen Meisterwerken verkörpert diese Form Stabilität, Beständigkeit und mathematische Eleganz. Die mathematischen Beziehungen zwischen Grundfläche, Höhe und den verschiedenen Seitenlängen folgen einfachen, aber kraftvollen Prinzipien, die auf dem Satz des Pythagoras basieren und zeigen, wie Geometrie und praktische Anwendung perfekt zusammenfinden.
Die Geometrie der Stabilität
Die quadratische Pyramide zeigt die Perfektion der strukturellen Stabilität:
- Quadratische Basis: Optimale Flächenverteilung für maximale Stabilität
- Dreieckige Seitenflächen: Natürlich stabile geometrische Form
- Zentraler Aufbau: Alle Kräfte konvergieren zur Spitze
- Symmetrie: Vierfache Rotationssymmetrie um die Höhenachse
- Konvexität: Keine strukturellen Schwachstellen
- Skalierbarkeit: Proportionen bleiben bei jeder Größe erhalten
- Universalität: In Natur und Technik weit verbreitet
Mathematische Eleganz
Pythagoras in Aktion
Die Formeln der quadratischen Pyramide basieren auf dem Satz des Pythagoras, der die Beziehungen zwischen den verschiedenen Höhen und Radien elegant beschreibt.
Volumen-Prinzip
Das Volumen folgt dem einfachen Prinzip: Ein Drittel der Grundfläche mal Höhe - eine der grundlegendsten Beziehungen der Geometrie.
Praktische Anwendbarkeit
Die klaren mathematischen Beziehungen machen die Pyramide ideal für Konstruktionen, bei denen Stabilität und Berechenbarkeit wichtig sind.
Kulturelle Bedeutung
Als eine der ältesten und bedeutendsten geometrischen Formen verbindet die Pyramide Mathematik, Architektur und kulturelle Symbolik.
Zusammenfassung
Die quadratische Pyramide ist mehr als nur eine geometrische Form - sie ist ein Symbol für die Verbindung von Mathematik und menschlicher Kultur. Ihre mathematischen Eigenschaften, basierend auf einfachen aber kraftvollen Prinzipien wie dem Satz des Pythagoras, machen sie zu einer der stabilsten und praktischsten Formen in der Geometrie. Von den antiken Wundern der Welt bis zu modernen architektonischen Innovationen bleibt die quadratische Pyramide ein faszinierendes Beispiel dafür, wie mathematische Eleganz und praktische Anwendung Hand in Hand gehen. Ihre Bedeutung reicht weit über die reine Berechnung hinaus und zeigt, wie Geometrie unsere Welt formt und unsere Kultur prägt.
|
|
|
|