Fünfeckpyramide Rechner
Rechner und Formeln zur Berechnung einer regelmäßigen Fünfeckpyramide
Pentagon Pyramide Rechner
Die Regelmäßige Fünfeckpyramide
Die regelmäßige Fünfeckpyramide ist eine Pyramide mit regelmäßigem Pentagon als Basis und fünf gleichschenkligen Dreiecken als Mantelfläche.
Pentagon Pyramide Eigenschaften
Goldener Schnitt Geometrie: Pentagon-Basis mit fünf gleichschenkligen Dreiecken
Pentagon Pyramide Struktur
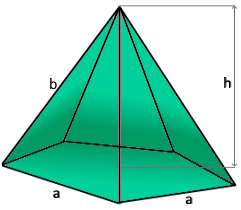
Die Pentagon-Pyramide mit goldenem Schnitt.
Fünf gleichschenklige Dreiecke als Mantel.
|
|
Was ist eine regelmäßige Fünfeckpyramide?
Die regelmäßige Fünfeckpyramide ist ein faszinierender geometrischer Körper:
- Definition: Pyramide mit regelmäßigem Pentagon als Grundfläche
- Struktur: 1 Pentagon-Basis + 5 gleichschenklige Dreiecke
- Goldener Schnitt: Pentagon verkörpert φ-Proportionen
- Ecken: 6 Ecken (5 Basis + 1 Spitze)
- Kanten: 10 Kanten (5 Pentagon + 5 Pyramide)
- Symmetrie: Fünfzählige Rotationssymmetrie
Geometrische Eigenschaften der Pentagon Pyramide
Die regelmäßige Fünfeckpyramide zeigt bemerkenswerte geometrische Eigenschaften:
Grundparameter
- Flächen: 6 Flächen (1 Pentagon + 5 Dreiecke)
- Ecken: 6 Ecken (5 Basis + 1 Spitze)
- Kanten: 10 Kanten (5+5)
- Euler-Charakteristik: V - E + F = 6 - 10 + 6 = 2
Besondere Eigenschaften
- Pentagon-Basis: Regelmäßiges Fünfeck mit φ-Verhältnissen
- Gleichschenklige Seiten: Alle Mantelflächen identisch
- Goldene Proportionen: Pentagon zeigt Goldenen Schnitt
- Konvex: Alle Kanten und Ecken ragen nach außen
Mathematische Beziehungen
Die regelmäßige Fünfeckpyramide folgt den mathematischen Gesetzen des Pentagons:
Pentagon-Trigonometrie
Verwendet spezielle trigonometrische Werte des Pentagons.
Goldener Schnitt
Pentagon-Geometrie ist direkt mit dem Goldenen Schnitt verknüpft.
Anwendungen der Pentagon Pyramide
Fünfeckpyramiden finden Anwendung in verschiedenen Bereichen:
Architektur & Design
- Moderne Gebäudespitzen
- Pentagon-inspirierte Dächer
- Skulpturale Elemente
- Dekorative Strukturen
Wissenschaft & Natur
- Kristallographische Formen
- Biologische Strukturen
- Molekulare Geometrie
- Optische Prismen
Bildung & Mathematik
- Goldener Schnitt Studien
- Pentagon-Geometrie
- 3D-Modellierung
- Pyramiden-Klassifikation
Kunst & Symbolik
- Geometrische Skulpturen
- Spirituelle Symbole
- Pentagon-basierte Kunst
- Dekorative Objekte
Formeln zur regelmäßigen Fünfeckpyramide
Mantelhöhe (s)
Höhe der Seitenflächen mit Pentagon-Kotangens
Kantenlänge (b)
Länge der Pyramidenkanten zur Spitze
Grundfläche (A)
Fläche des regelmäßigen Pentagons
Eine Seitenfläche (As)
Fläche eines gleichschenkligen Dreiecks
Mantelfläche (Am)
Summe aller fünf Seitenflächen
Oberfläche (S)
Grundfläche plus Mantelfläche
Umfang (P)
Umfang des regelmäßigen Pentagons
Volumen (V)
Ein Drittel der Grundfläche mal Höhe
Berechnungsbeispiel für eine regelmäßige Fünfeckpyramide
Gegeben
Gesucht: Alle Eigenschaften der regelmäßigen Fünfeckpyramide
1. Grundfläche-Berechnung
Für a = 8:
\[A = \frac{5 \cdot 8^2}{4 \cdot \tan\left(\frac{\pi}{5}\right)}\] \[\tan\left(\frac{\pi}{5}\right) ≈ 0.726\] \[A = \frac{320}{2.904} ≈ 110.2\]Die Grundfläche beträgt etwa 110.2 Flächeneinheiten
2. Mantelhöhe-Berechnung
Für a = 8, h = 10:
\[s = \sqrt{10^2 + \frac{8^2 \cdot \cot^2\left(\frac{\pi}{5}\right)}{4}}\] \[\cot\left(\frac{\pi}{5}\right) ≈ 1.376\] \[s = \sqrt{100 + \frac{64 \cdot 1.894}{4}} ≈ 12.1\]Die Mantelhöhe beträgt etwa 12.1 Längeneinheiten
3. Kantenlänge-Berechnung
Für s ≈ 12.1, a = 8:
\[b = \sqrt{12.1^2 + \frac{8^2}{4}}\] \[b = \sqrt{146.41 + 16}\] \[b ≈ \sqrt{162.41} ≈ 12.7\]Die Kantenlänge beträgt etwa 12.7 Längeneinheiten
4. Mantelfläche-Berechnung
Für a = 8, s ≈ 12.1:
\[A_m = \frac{5 \cdot 8 \cdot 12.1}{2}\] \[A_m = \frac{484}{2}\] \[A_m = 242\]Die Mantelfläche beträgt etwa 242 Flächeneinheiten
5. Oberfläche-Berechnung
A ≈ 110.2, Am ≈ 242:
\[S = A + A_m\] \[S = 110.2 + 242\] \[S ≈ 352.2\]Die Oberfläche beträgt etwa 352.2 Flächeneinheiten
6. Volumen-Berechnung
A ≈ 110.2, h = 10:
\[V = \frac{A \cdot h}{3}\] \[V = \frac{110.2 \cdot 10}{3}\] \[V ≈ 367.3\]Das Volumen beträgt etwa 367.3 Volumeneinheiten
Zusammenfassung der Ergebnisse
Die regelmäßige Fünfeckpyramide mit Pentagon-Basis und goldenem Schnitt
Die regelmäßige Fünfeckpyramide: Pentagon trifft Pyramide
Die regelmäßige Fünfeckpyramide ist ein außergewöhnlicher geometrischer Körper, der die elegante Schönheit des regelmäßigen Pentagons mit der klassischen Form der Pyramide verbindet. Mit ihrer fünfeckigen Basis, die den Goldenen Schnitt φ = (1+√5)/2 verkörpert, und ihren fünf gleichschenkligen Dreiecksflächen schafft sie eine harmonische Verbindung zwischen der Zwei- und Dreidimensionalität. Ihre mathematischen Formeln mit Pentagon-spezifischen trigonometrischen Werten wie tan(π/5) und cot(π/5) zeigen die tiefe Verwurzelung in der Geometrie des Goldenen Schnitts und machen sie zu einem faszinierenden Studienobjekt.
Die Geometrie des Pentagon-Pyramiden-Hybrids
Die regelmäßige Fünfeckpyramide zeigt die perfekte Synthese verschiedener geometrischer Prinzipien:
- Pentagon-Basis: Regelmäßiges Fünfeck mit Goldenen-Schnitt-Proportionen
- Pyramidale Struktur: Klassische Pyramidenform mit einer Spitze
- Fünfzählige Symmetrie: Rotationssymmetrie um die zentrale Achse
- Gleichschenklige Mantelflächen: Fünf identische Dreiecksflächen
- Goldene Proportionen: φ-Verhältnisse in der Pentagon-Basis
- Trigonometrische Eleganz: Spezielle Winkel π/5 (36°)
- Harmonische Balance: Perfekte Verteilung von Masse und Form
Pentagon-Mathematik und Pyramiden-Geometrie
Pentagon-Trigonometrie
Die Verwendung von tan(π/5) ≈ 0.726 und cot(π/5) ≈ 1.376 verbindet die Pyramide direkt mit dem Goldenen Schnitt des Pentagons.
Klassische Pyramiden-Formeln
Die Volumenformel V = A·h/3 zeigt die klassische Pyramiden-Mathematik, angewendet auf die Pentagon-Basis.
Geometrische Harmonie
Die Kombination aus Pentagon-Basis und pyramidaler Struktur schafft eine einzigartige geometrische Harmonie.
Goldene Verbindungen
Das Pentagon als Basis bringt die φ-Proportionen in die dreidimensionale Pyramidenform.
Zusammenfassung
Die regelmäßige Fünfeckpyramide steht als faszinierendes Beispiel für die Vereinigung verschiedener geometrischer Traditionen. Ihre Pentagon-Basis mit den charakteristischen φ-Proportionen, kombiniert mit der klassischen Pyramidenstruktur, macht sie zu einem einzigartigen geometrischen Hybrid. Von der antiken Geometrie des Goldenen Schnitts bis zur modernen Architektur zeigt sie, wie mathematische Eleganz und praktische Anwendbarkeit Hand in Hand gehen können. Ihre trigonometrischen Formeln mit Pentagon-spezifischen Werten demonstrieren die tiefe mathematische Struktur, die dieser scheinbar einfachen, aber außerordentlich reichen Form zugrunde liegt. In der Welt der geometrischen Körper verkörpert die regelmäßige Fünfeckpyramide die perfekte Balance zwischen der zweidimensionalen Schönheit des Pentagons und der dreidimensionalen Majestät der Pyramide.
|
|
|
|