Sechseckige Pyramide Rechner
Rechner und Formeln zur Berechnung einer regelmäßigen Sechseckpyramide
Sechseckpyramide Rechner
Die Regelmäßige Sechseckpyramide
Eine regelmäßige Sechseckpyramide hat ein gleichseitiges Sechseck als Basis und sechs gleichschenklige Dreiecke als Mantelfläche.
Sechseckpyramide Eigenschaften
Die klassische Sechseckpyramide: Ein Sechseck als Basis mit sechs Dreiecksflächen
Sechseckpyramide Struktur
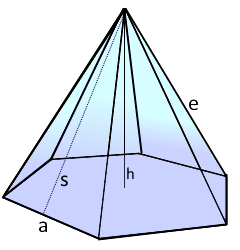
Die regelmäßige Sechseckpyramide mit eleganter Form.
Sechseckige Basis mit sechs Dreiecksflächen.
|
|
Was ist eine regelmäßige Sechseckpyramide?
Eine regelmäßige Sechseckpyramide ist ein faszinierender geometrischer Körper:
- Definition: Pyramide mit regelmäßigem Sechseck als Basis
- Basis: Gleichseitiges Sechseck als Grundfläche
- Mantelflächen: 6 kongruente gleichschenklige Dreiecke
- Ecken: 7 Ecken (6 Basis + 1 Spitze)
- Kanten: 12 Kanten (6 Basis + 6 Seiten)
- Symmetrie: Sechsfache Rotationssymmetrie
Geometrische Eigenschaften der Sechseckpyramide
Die regelmäßige Sechseckpyramide zeigt bemerkenswerte geometrische Eigenschaften:
Grundparameter
- Flächen: 7 Flächen (1 Sechseck + 6 Dreiecke)
- Ecken: 7 Ecken (6 Basis + 1 Apex)
- Kanten: 12 Kanten (6+6)
- Euler-Charakteristik: V - E + F = 7 - 12 + 7 = 2
Besondere Eigenschaften
- Hexagonal: Sechseckige Symmetrie
- Konvex: Alle Kanten ragen nach außen
- Regelmäßig: Symmetrische Seitenflächen
- Elegant: Harmonische Proportionen
Mathematische Beziehungen
Die regelmäßige Sechseckpyramide folgt eleganten mathematischen Gesetzen:
Volumen-Beziehung
Das Volumen verwendet die hexagonale Grundfläche. Elegant mit √3-Beziehung.
Flächen-Beziehungen
Alle Flächenformeln verwenden π/6 Winkel. Hexagonale Harmonie.
Anwendungen der Sechseckpyramide
Regelmäßige Sechseckpyramiden finden Anwendung in verschiedenen Bereichen:
Architektur & Bauwesen
- Dachkonstruktionen und Türme
- Dekorative Pyramidenspitzen
- Strukturelle Elemente
- Moderne Architekturformen
Wissenschaft & Technik
- Kristallographische Strukturen
- Optische Prismen
- Mechanische Komponenten
- Ingenieurskonstruktionen
Bildung & Lehre
- Geometrie-Unterricht
- 3D-Modellierung
- Mathematische Demonstrationen
- Pyramiden-Studien
Kunst & Design
- Skulpturale Formen
- Dekorative Objekte
- Produktdesign
- Geometrische Kunstwerke
Formeln zur regelmäßigen Sechseckpyramide
Mantelhöhe (s)
Schräge Höhe mit cot(π/6) = √3
Kantenlänge (e)
Länge der Pyramidenkanten
Grundfläche (A)
Fläche des regelmäßigen Sechsecks
Eine Seitenfläche (As)
Fläche eines gleichschenkligen Dreiecks
Mantelfläche (Am)
Gesamtfläche aller Seitenflächen
Oberfläche (S)
Grundfläche plus Mantelfläche
Umfang (P)
Umfang des Sechsecks
Volumen (V)
Ein Drittel von Grundfläche mal Höhe
Berechnungsbeispiel für eine regelmäßige Sechseckpyramide
Gegeben
Gesucht: Alle Eigenschaften der Sechseckpyramide
1. Grundfläche-Berechnung
Sechseckfläche:
\[A = \frac{3\sqrt{3}a^2}{2}\] \[A = \frac{3\sqrt{3} \cdot 8^2}{2}\] \[A = \frac{3\sqrt{3} \cdot 64}{2} ≈ 166.28\]Die Grundfläche beträgt etwa 166.28 Flächeneinheiten
2. Mantelhöhe-Berechnung
Mit cot(π/6) = √3:
\[s = \sqrt{h^2 + \frac{a^2 \cdot 3}{4}}\] \[s = \sqrt{10^2 + \frac{64 \cdot 3}{4}}\] \[s = \sqrt{100 + 48} = \sqrt{148} ≈ 12.17\]Die Mantelhöhe beträgt etwa 12.17 Einheiten
3. Volumen-Berechnung
Ein Drittel der Basis mal Höhe:
\[V = \frac{A \cdot h}{3}\] \[V = \frac{166.28 \cdot 10}{3}\] \[V ≈ 554.3\]Das Volumen beträgt etwa 554.3 Volumeneinheiten
4. Die perfekte Sechseckpyramide
Die regelmäßige Sechseckpyramide mit eleganter Geometrie
Die regelmäßige Sechseckpyramide: Die Eleganz der hexagonalen Geometrie
Die regelmäßige Sechseckpyramide ist ein faszinierender geometrischer Körper, der die Eleganz der hexagonalen Symmetrie mit der klassischen Pyramidenform vereint. Mit einem regelmäßigen Sechseck als Basis und sechs kongruenten gleichschenkligen Dreiecken als Mantelflächen verkörpert sie die perfekte Balance zwischen Stabilität und ästhetischer Schönheit. Die mathematischen Beziehungen, die durch die Quadratwurzel von 3 und die trigonometrischen Funktionen des 30°-Winkels (π/6) geprägt sind, machen sie zu einem idealen Studienobjekt für die Geometrie und ihre praktischen Anwendungen.
Die Geometrie der hexagonalen Perfektion
Die regelmäßige Sechseckpyramide zeigt die Schönheit der hexagonalen Symmetrie:
- Hexagonale Basis: Das regelmäßige Sechseck als optimale Grundform
- Sechsfache Symmetrie: Rotationssymmetrie um 60°-Schritte
- Kongruente Flächen: Sechs identische gleichschenklige Dreiecke
- Optimale Stabilität: Ideale Lastverteilung durch hexagonale Struktur
- Natürliche Form: Verwandtschaft zu Kristallstrukturen und Bienenwaben
- Mathematische Eleganz: √3-Beziehungen in allen Formeln
- Konstruktive Perfektion: Einfache Herstellung und Berechnung
Mathematische Eleganz
Quadratwurzel-3-Harmonie
Alle Formeln der Sechseckpyramide sind durch die elegante √3-Beziehung verbunden, die aus cot(π/6) = √3 und tan(π/6) = 1/√3 resultiert.
Hexagonale Mathematik
Die sechseckige Basis folgt den natürlichen Gesetzen der hexagonalen Geometrie, die in der Natur weit verbreitet ist.
Strukturelle Optimalität
Die hexagonale Struktur bietet optimale Material-Effizienz und Stabilität, wie in Bienenwaben und Kristallgittern zu sehen.
Ästhetische Perfektion
Die harmonischen Proportionen und die natürliche Schönheit der Sechseckpyramide machen sie zu einer beliebten Form in Architektur und Design.
Zusammenfassung
Die regelmäßige Sechseckpyramide verkörpert die perfekte Synthese zwischen natürlicher Schönheit und mathematischer Präzision. Ihre hexagonale Basis und die sechs gleichschenkligen Dreiecksflächen, beschrieben durch elegante √3-Beziehungen, machen sie zu einem faszinierenden Studienobjekt der Geometrie. Von den antiken Bauwerken bis zu modernen architektonischen Meisterwerken zeigt die Sechseckpyramide ihre zeitlose Eleganz und praktische Anwendbarkeit. Die mathematische Schönheit ihrer Formeln, die natürliche Verwandtschaft zur hexagonalen Strukturen in der Natur und die optimale Balance zwischen Ästhetik und Funktionalität machen sie zu einem der faszinierendsten geometrischen Körper in der dreidimensionalen Geometrie.
|
|
|
|