Rechteckiger Pyramidenstumpf Rechner
Rechner und Formeln zur Berechnung der Parameter eines rechteckigen Pyramidenstumpf
Rechteckiger Pyramidenstumpf Rechner
Der rechteckige Pyramidenstumpf
Diese Funktion berechnet das Volumen und alle Oberflächen eines rechteckigen Pyramidenstumpf. Zur Berechnung geben Sie die Höhe und alle vier Seitenlängen ein.
Rechteckiger Pyramidenstumpf Eigenschaften
Der rechteckige Frustum: Entstanden durch horizontalen Schnitt durch eine rechteckige Pyramide
Rechteckiger Pyramidenstumpf Struktur
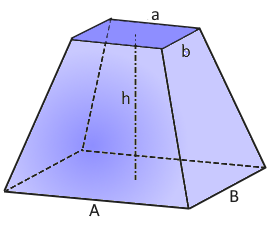
Der rechteckige Pyramidenstumpf (Frustum).
Maximal vielseitige Form durch Rechteck-Basis.
Was ist ein rechteckiger Pyramidenstumpf?
Der rechteckige Pyramidenstumpf ist die vielseitigste Form aller Pyramidenstümpfe:
- Definition: Entsteht durch horizontalen Schnitt durch eine rechteckige Pyramide
- Struktur: Zwei parallele Rechtecke unterschiedlicher Größe
- Flächen: 2 Rechtecke (Basis + Deckfläche) + 4 Trapeze (Seitenflächen)
- Ecken: 8 Ecken (4 unten + 4 oben)
- Kanten: 12 Kanten (4 unten + 4 oben + 4 seitlich)
- Besonderheit: Maximale Flexibilität durch vier verschiedene Parameter
Geometrische Eigenschaften des rechteckigen Pyramidenstumpfs
Der rechteckige Pyramidenstumpf zeigt die maximale geometrische Flexibilität:
Grundparameter
- Flächen: 6 (2 Rechtecke + 4 Trapeze)
- Ecken: 8 (4 unten + 4 oben)
- Kanten: 12 (4+4+4)
- Euler-Charakteristik: V - E + F = 8 - 12 + 6 = 2
Besondere Eigenschaften
- Vielseitigkeit: Vier verschiedene Seitenlängen
- Asymmetrie: Unterschiedliche Trapezformen möglich
- Anpassbarkeit: Optimierbar für spezielle Anwendungen
- Komplexität: Reichste Geometrie aller Pyramidenstümpfe
Mathematische Beziehungen
Der rechteckige Pyramidenstumpf folgt komplexen, aber eleganten mathematischen Gesetzen:
Volumen-Formel
Kombiniert alle vier Seitenlängen. Komplexeste Frustum-Formel.
Mantelflächen-Formel
Vier individuelle Trapezflächen. Jeweils eigene Schräghöhe.
Anwendungen des rechteckigen Pyramidenstumpfs
Rechteckige Pyramidenstümpfe finden vielseitige Anwendung:
Architektur & Bauwesen
- Asymmetrische Fundamente
- Spezielle Böschungen
- Moderne Gebäudeformen
- Brückenpfeiler
Technik & Industrie
- Spezielle Behälter und Trichter
- Gießformen für komplexe Teile
- Angepasste Förderanlagen
- Maschinenbaukomponenten
Bildung & Lehre
- Erweiterte Geometrie-Beispiele
- Komplexe Volumenberechnungen
- 3D-Geometrie-Herausforderungen
- Ingenieurs-Mathematik
Design & Anwendung
- Individuelle Skulpturen
- Spezialmöbel
- Landschaftsarchitektur
- Produktdesign mit Funktion
Formeln zum rechteckigen Pyramidenstumpf
Volumen (V)
Komplexe Formel mit Kreuzprodukten der Seitenlängen
Mantelfläche (AL)
Summe zweier Trapezpaare mit unterschiedlichen Schräghöhen
Oberfläche (S)
Mantelfläche plus beide rechteckige Flächen
Basisfläche und Deckfläche
Einfache Rechteckflächen
Zusätzliche Parameter
\(s_1 = \sqrt{\left(\frac{A-a}{2}\right)^2 + h^2}\)
\(s_2 = \sqrt{\left(\frac{B-b}{2}\right)^2 + h^2}\)
\(P_{Basis} = 2(A+B)\)
\(P_{Deck} = 2(a+b)\)
Alle Parameter berücksichtigen die rechteckige Asymmetrie
Berechnungsbeispiel für einen rechteckigen Pyramidenstumpf
Gegeben
Gesucht: Alle Eigenschaften des rechteckigen Pyramidenstumpfs
1. Volumen-Berechnung
Für a=4, b=3, A=6, B=5, h=5:
\[V = \frac{(Ab + aB + 2\sqrt{ab \cdot AB}) \cdot h}{6}\] \[= \frac{(6 \cdot 3 + 4 \cdot 5 + 2\sqrt{4 \cdot 3 \cdot 6 \cdot 5}) \cdot 5}{6}\] \[= \frac{(18 + 20 + 2\sqrt{360}) \cdot 5}{6}\] \[= \frac{(38 + 2 \cdot 18.97) \cdot 5}{6} ≈ \frac{75.94 \cdot 5}{6} ≈ 63.28\]Das Volumen beträgt etwa 63.28 Volumeneinheiten
2. Schräghöhen-Berechnung
Schräghöhen der Trapeze:
\[s_1 = \sqrt{\left(\frac{A-a}{2}\right)^2 + h^2} = \sqrt{\left(\frac{6-4}{2}\right)^2 + 5^2}\] \[= \sqrt{1^2 + 25} = \sqrt{26} ≈ 5.10\] \[s_2 = \sqrt{\left(\frac{B-b}{2}\right)^2 + h^2} = \sqrt{\left(\frac{5-3}{2}\right)^2 + 5^2}\] \[= \sqrt{1^2 + 25} = \sqrt{26} ≈ 5.10\]Beide Schräghöhen betragen etwa 5.10 Längeneinheiten
3. Mantelflächen-Berechnung
Vier trapezförmige Seitenflächen:
\[A_L = (a+A) \cdot s_1 + (b+B) \cdot s_2\] \[= (4+6) \cdot 5.10 + (3+5) \cdot 5.10\] \[= 10 \cdot 5.10 + 8 \cdot 5.10\] \[= 51 + 40.8 = 91.8\]Die Mantelfläche beträgt etwa 91.8 Flächeneinheiten
4. Rechteckflächen-Berechnung
Basis- und Deckfläche:
Basisfläche: \(A_{Basis} = A \cdot B = 6 \cdot 5 = 30\)Deckfläche: \(A_{Deck} = a \cdot b = 4 \cdot 3 = 12\)
Oberfläche: \(S = A_L + A_{Basis} + A_{Deck}\) \[= 91.8 + 30 + 12 = 133.8\]
Basisfläche: 30, Deckfläche: 12, Oberfläche: 133.8
5. Zusätzliche Parameter
Weitere interessante Werte:
Basis-Umfang: \(P_{Basis} = 2(A+B) = 2(6+5) = 22\)Deck-Umfang: \(P_{Deck} = 2(a+b) = 2(4+3) = 14\)
Verhältnis Deck/Basis: \(\frac{12}{30} = 0.4\)
Basis-Umfang: 22, Deck-Umfang: 14, Flächenverhältnis: 40%
6. Der perfekte rechteckige Pyramidenstumpf
Der rechteckige Pyramidenstumpf mit maximaler Flexibilität
Der rechteckige Pyramidenstumpf: Maximale geometrische Vielseitigkeit
Der rechteckige Pyramidenstumpf ist die komplexeste und vielseitigste Form aller Pyramidenstümpfe. Mit vier unabhängigen Seitenlängen-Parametern bietet er maximale Flexibilität für spezialisierte Anwendungen. Diese geometrische Form entsteht durch das horizontale Abschneiden einer rechteckigen Pyramide und vereint die Vorteile einer stabilen Basis mit der Funktionalität unterschiedlicher Ober- und Unterflächen. Die mathematischen Beziehungen sind entsprechend komplex, aber folgen klaren Prinzipien, die auf der Ähnlichkeit der parallelen Rechtecke und den vier unterschiedlichen trapezförmigen Verbindungsflächen basieren.
Die Geometrie der maximalen Flexibilität
Der rechteckige Pyramidenstumpf zeigt die Perfektion der anpassbaren Geometrie:
- Vier Parameter: Maximale Kontrolle durch vier unabhängige Seitenlängen
- Asymmetrische Trapeze: Bis zu vier verschiedene Trapezformen möglich
- Rechteckige Basis: Optimale Flächenausnutzung für spezielle Anwendungen
- Individuelle Schräghöhen: Zwei verschiedene Schräghöhen für die Trapezpaare
- Strukturelle Anpassung: Optimierbar für verschiedenste Belastungsarten
- Geometrische Komplexität: Reichste mathematische Beziehungen
- Praktische Vielseitigkeit: Adaptierbar für speziellste Anforderungen
Mathematische Komplexität
Volumen-Komplexität
Die Volumenformel V = ⅙h(Ab + aB + 2√(ab·AB)) ist die komplexeste aller Frustum-Formeln und berücksichtigt alle Kreuzbeziehungen zwischen den Seitenlängen.
Mantelflächen-Vielfalt
Die Mantelfläche setzt sich aus vier individuellen Trapezen zusammen, die jeweils ihre eigenen Schräghöhen und Proportionen haben können.
Anwendungs-Optimierung
Die vier unabhängigen Parameter ermöglichen die Optimierung für spezielle Anwendungen, wo andere Frustum-Formen nicht ausreichen.
Ingenieurs-Geometrie
Diese Form repräsentiert die Spitze der praktischen Geometrie, wo mathematische Komplexität maximale Anwendungsflexibilität ermöglicht.
Zusammenfassung
Der rechteckige Pyramidenstumpf ist der Höhepunkt der Frustum-Geometrie. Seine vier unabhängigen Seitenlängen-Parameter ermöglichen eine Flexibilität, die kein anderer Pyramidenstumpf bieten kann. Die mathematischen Formeln sind entsprechend komplex, aber sie folgen klaren Prinzipien und ermöglichen präzise Berechnungen für auch die speziellsten Anwendungen. Von asymmetrischen Fundamenten im Bauwesen über spezialisierte Behälter in der Industrie bis hin zu individuellen Designlösungen zeigt diese Form, wie mathematische Komplexität zu praktischer Vielseitigkeit führt. Der rechteckige Pyramidenstumpf ist damit das perfekte Werkzeug für Ingenieure und Designer, die maximale geometrische Kontrolle benötigen. Seine Bedeutung liegt nicht nur in der reinen Berechnung, sondern in der Möglichkeit, für jede Anwendung die optimal angepasste Form zu schaffen.
|
|