Regelmäßigen Pyramidenstumpf berechnen

Rechner und Formeln zur Berechnung eines regelmäßigen Pyramidenstumpfs

Die abgeschnittene Pyramide - Eleganz der Geometrie!

Pyramidenstumpf Rechner

Der Regelmäßige Pyramidenstumpf

Ein regelmäßiger Pyramidenstumpf entsteht durch das horizontale Abschneiden einer regelmäßigen Pyramide mit einem regelmäßigen Vieleck als Basis.

Parameter eingeben

Seitenlänge Basis a

Seitenlänge der Grundfläche

Seitenlänge Dach b

Seitenlänge der Deckfläche

Höhe h

Höhe des Pyramidenstumpfs

Ecken Anzahl n

Anzahl der Ecken des Vielecks

Dezimalstellen

Pyramidenstumpf Berechnungsergebnisse

Mantelhöhe s:

Kantenlänge e:

Seitenfläche A_s:

Mantelfläche A_m:

Oberfläche S:

Umfang P:

Volumen V:

Pyramidenstumpf Eigenschaften

Die abgeschnittene Pyramide: Zwei parallele regelmäßige Vielecke verbunden

Regelmäßige Basis Parallele Deckfläche Trapezförmige Seiten Elegante Geometrie

Pyramidenstumpf Struktur

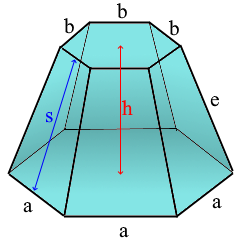
Der regelmäßige Pyramidenstumpf mit eleganter Form.
Abgeschnittene regelmäßige Pyramide.

Was ist ein regelmäßiger Pyramidenstumpf?

Ein regelmäßiger Pyramidenstumpf ist ein faszinierender geometrischer Körper:

Definition: Abgeschnittene regelmäßige Pyramide
Basis: Regelmäßiges n-Eck als Grundfläche
Dach: Kleineres, paralleles n-Eck als Deckfläche

Seitenflächen: n kongruente Trapeze
Symmetrie: Rotations- und Spiegelsymmetrie
Anwendung: Architektur, Technik und Design

Geometrische Eigenschaften des Pyramidenstumpfs

Der regelmäßige Pyramidenstumpf zeigt bemerkenswerte geometrische Eigenschaften:

Grundparameter

Flächen: 2 regelmäßige n-Ecke + n Trapeze
Ecken: 2n Ecken (n oben, n unten)
Kanten: 3n Kanten (n+n+n)
Euler-Formel: V - E + F = 2n - 3n + (n+2) = 2

Besondere Eigenschaften

Prismatoid: Spezielle Form des Prismatoids
Ähnlichkeit: Basis und Dach sind ähnlich
Konvergenz: Seitenkanten treffen sich in einem Punkt
Stabilität: Sehr stabile Bauform

Mathematische Beziehungen

Der regelmäßige Pyramidenstumpf folgt eleganten mathematischen Gesetzen:

Volumen-Beziehung

Simpsons Regel

Das Volumen folgt der Simpsonsche Regel mit drei Termen. Elegant und präzise.

Flächen-Beziehungen

Trigonometrie

Alle Flächenformeln verwenden Tangens und Kotangens. Mathematische Eleganz.

Anwendungen des Pyramidenstumpfs

Regelmäßige Pyramidenstümpfe finden Anwendung in verschiedenen Bereichen:

Architektur & Bauwesen

Stufenpyramiden und Tempel
Moderne Gebäudearchitektur
Brückenpfeiler und Fundamente
Dekorative Baukomponenten

Technik & Industrie

Behälter und Trichter
Maschinenbauteile
Optische Komponenten
Strömungstechnische Elemente

Bildung & Lehre

Geometrie-Unterricht
3D-Geometrie-Studien
Volumenberechnung
Polyeder-Klassifikation

Kunst & Design

Skulpturale Formen
Moderne Kunstwerke
Produktdesign
Architektonische Details

Formeln zum regelmäßigen Pyramidenstumpf

Mantelhöhe (s)

\[s=\sqrt{\frac{1}{4} \cdot \cot^2\left(\frac{\pi}{n} \right) \cdot ( a - b )^2 + h^2} \]

Schräge Höhe der Seitenflächen mit Kotangens

Kantenlänge (e)

\[e =\sqrt{\frac{4 \cdot s^2 + ( a - b )^2 }{4}}\]

Länge der schrägen Kanten des Stumpfs

Basis- und Dachfläche (A)

\[A = n \cdot \frac{a^2 + b^2}{4 \cdot \tan(\frac{\pi}{n})} \]

Summe von Grund- und Deckfläche

Eine Seitenfläche (A_s)

\[A_s = \frac{(a + b) \cdot s}{2} \]

Fläche einer trapezförmigen Seitenfläche

Mantelfläche (A_m)

\[A_m = n \cdot A_s \]

Gesamtfläche aller Seitenflächen

Oberfläche (S)

\[S = A + A_m \]

Gesamtoberfläche des Pyramidenstumpfs

Umfang (P)

\[P = n \cdot a \]

Umfang der Grundfläche

Volumen (V)

\[V = \frac{h}{3} \cdot \left( \frac{n \cdot( a^2 + b^2) }{ 4 \cdot \tan(\frac{\pi}{n})} + \sqrt{\frac{n^2 \cdot a^2 \cdot b^2}{(4 \cdot \tan(\frac{\pi}{n}))^2}} \right) \]

Volumen nach der Simpsonsche Regel

Berechnungsbeispiel für einen regelmäßigen Pyramidenstumpf

Gegeben

Basis-Seitenlänge a = 8 Dach-Seitenlänge b = 5 Höhe h = 6 Ecken n = 5 (Pentagon)

Gesucht: Alle Eigenschaften des fünfeckigen Pyramidenstumpfs

1. Mantelhöhe-Berechnung

Für Pentagon (n = 5):

\[s = \sqrt{\frac{1}{4} \cdot \cot^2\left(\frac{\pi}{5} \right) \cdot (8-5)^2 + 6^2}\] \[s = \sqrt{\frac{1}{4} \cdot 2.377^2 \cdot 9 + 36}\] \[s ≈ \sqrt{12.78 + 36} ≈ 6.98\]

Die Mantelhöhe beträgt etwa 6.98 Einheiten

2. Volumen-Berechnung

Mit Simpsonsche Regel:

\[V = \frac{6}{3} \cdot \left( \frac{5 \cdot (64 + 25)}{4 \cdot \tan(\frac{\pi}{5})} + \sqrt{\frac{25 \cdot 64 \cdot 25}{(4 \cdot 0.726)^2}} \right)\] \[V = 2 \cdot (153.72 + 37.27)\] \[V ≈ 382.0\]

Das Volumen beträgt etwa 382.0 Volumeneinheiten

3. Oberflächen-Berechnung

Basis + Dach + Mantel:

\[A = 5 \cdot \frac{64 + 25}{4 \cdot 0.726} ≈ 153.7\] \[A_m = 5 \cdot \frac{(8+5) \cdot 6.98}{2} ≈ 227.2\] \[S = 153.7 + 227.2 ≈ 380.9\]

Die Oberfläche beträgt etwa 380.9 Flächeneinheiten

4. Der perfekte Pyramidenstumpf

Basis a = 8.0 Dach b = 5.0 Höhe h = 6.0

Volumen V ≈ 382.0 Oberfläche S ≈ 380.9 🏛️ Pentagon

Der fünfeckige Pyramidenstumpf mit eleganter Geometrie

Der regelmäßige Pyramidenstumpf: Die abgeschnittene Perfektion

Der regelmäßige Pyramidenstumpf ist ein faszinierender geometrischer Körper, der durch das horizontale Abschneiden einer regelmäßigen Pyramide entsteht. Diese elegante Form vereint die Stabilität einer breiten Basis mit der Eleganz einer sich verjüngenden Struktur und findet sowohl in der antiken Architektur als auch in modernen technischen Anwendungen vielseitige Verwendung. Die mathematische Schönheit liegt in den harmonischen Beziehungen zwischen Basis, Deckfläche und Höhe, die durch trigonometrische Funktionen und die Simpsonsche Regel elegant beschrieben werden.

Die Geometrie der Harmonie

Der regelmäßige Pyramidenstumpf zeigt die Perfektion der geometrischen Harmonie:

Prismatoid: Spezielle Form mit zwei parallelen, ähnlichen Grundflächen
Ähnlichkeit: Basis und Dach sind ähnliche regelmäßige Vielecke
Konvergenz: Alle Seitenkanten treffen sich in einem virtuellen Punkt
Symmetrie: n-fache Rotationssymmetrie um die Mittelachse
Stabilität: Optimale Lastverteilung durch Pyramidenform
Vielseitigkeit: Anpassbar an verschiedene Anwendungen
Eleganz: Ausgewogene Proportionen zwischen Basis und Spitze

Mathematische Eleganz

Simpsonsche Regel

Das Volumen folgt der eleganten Simpsonschen Regel, die drei charakteristische Terme harmonisch verbindet und präzise Berechnungen ermöglicht.

Trigonometrische Perfektion

Alle Flächenberechnungen verwenden Tangens und Kotangens, die die natürlichen Winkelbeziehungen im regelmäßigen Vieleck beschreiben.

Strukturelle Harmonie

Die mathematischen Beziehungen spiegeln die natürliche Harmonie und Stabilität des Pyramidenstumpfs wider.

Praktische Anwendung

Von antiken Tempeln bis zu modernen Industrieanlagen - der Pyramidenstumpf verbindet Ästhetik mit Funktionalität.

Zusammenfassung

Der regelmäßige Pyramidenstumpf verkörpert die perfekte Symbiose zwischen mathematischer Präzision und praktischer Anwendbarkeit. Seine Struktur aus zwei parallelen regelmäßigen Vielecken, verbunden durch trapezförmige Seitenflächen, wird durch elegante trigonometrische Formeln beschrieben. Von den monumentalen Stufenpyramiden der Antike bis zu den funktionalen Trichtern und Behältern der modernen Industrie zeigt der Pyramidenstumpf seine Vielseitigkeit und zeitlose Eleganz. Die mathematische Schönheit seiner Formeln, insbesondere die Anwendung der Simpsonschen Regel für das Volumen, macht ihn zu einem faszinierenden Studienobjekt, das Geometrie, Trigonometrie und praktische Anwendung harmonisch vereint.

Dreieckige Pyramide • Quadratische Pyramide • Fünfeckige Pyramide • Sechseckige Pyramide • Siebeneckige Pyramide • Regelmäßige Pyramide • Quadratischer Pyramidenstumpf • Rechteckiger Pyramidenstumpf • Regelmäßiger Pyramidenstumpf • Dreieckige Doppelpyramide • Fünfeckige Doppelpyramide • Sechseckige Doppelpyramide • Doppelpyramide • Frustum Pyramide