Regelmäßige Pyramide Rechner
Rechner und Formeln zur Berechnung einer regelmäßigen Pyramide
Regelmäßige Pyramide Rechner
Die regelmäßige Pyramide
Diese Funktion berechnet verschiedene Parameter einer regelmäßigen Pyramide. Die regelmäßige Pyramide hat ein regelmäßiges n-Eck als Basis. Geben Sie die Seitenlänge, Eckenanzahl und Höhe ein.
Regelmäßige Pyramide Eigenschaften
Die universelle Pyramide: Regelmäßiges n-Eck als Basis mit n dreieckigen Seitenflächen
Regelmäßige Pyramide Struktur
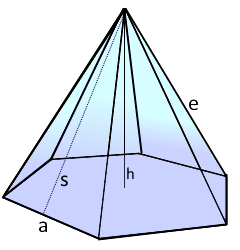
Die regelmäßige Pyramide mit n-Eck Basis.
Perfekte Symmetrie durch regelmäßiges Vieleck.
|
|
Was ist eine regelmäßige Pyramide?
Die regelmäßige Pyramide ist die universellste aller Pyramidenformen:
- Definition: Pyramide mit regelmäßigem n-Eck als Basis
- Basis: Regelmäßiges Vieleck mit n gleichen Seiten und Winkeln
- Flächen: 1 regelmäßiges n-Eck + n kongruente Dreiecke
- Ecken: n+1 Ecken (n Basis + 1 Spitze)
- Kanten: 2n Kanten (n Basis + n seitlich)
- Symmetrie: n-fache Rotationssymmetrie
Geometrische Eigenschaften der regelmäßigen Pyramide
Die regelmäßige Pyramide zeigt universelle geometrische Eigenschaften:
Grundparameter
- Flächen: n+1 (1 n-Eck + n Dreiecke)
- Ecken: n+1 (n Basis + 1 Spitze)
- Kanten: 2n (n Basis + n seitlich)
- Euler-Charakteristik: V - E + F = (n+1) - 2n + (n+1) = 2
Besondere Eigenschaften
- Universalität: Funktioniert für jedes n ≥ 3
- Symmetrie: n-fache Rotationssymmetrie
- Regularität: Alle Seitenflächen sind kongruent
- Skalierbarkeit: Trigonometrische Beziehungen
Mathematische Beziehungen
Die regelmäßige Pyramide folgt eleganten trigonometrischen Gesetzen:
Volumen-Formel
Basis-Fläche mit Tangens-Beziehung. Trigonometrie in Aktion.
Grundflächen-Formel
n-Eck Fläche mit Tangens. Universelle Vieleck-Formel.
Anwendungen der regelmäßigen Pyramide
Regelmäßige Pyramiden finden vielseitige Anwendung:
Architektur & Bauwesen
- Spezielle Dachkonstruktionen
- Turm- und Turmspitzen
- Dekorative Strukturelemente
- Moderne geometrische Gebäude
Wissenschaft & Technik
- Kristallographische Strukturen
- Optische Komponenten
- Antennen-Design
- 3D-Druck Anwendungen
Bildung & Lehre
- Trigonometrie-Anwendungen
- Vieleck-Geometrie
- 3D-Geometrie-Studien
- Symmetrie-Konzepte
Kunst & Design
- Geometrische Skulpturen
- Symmetrische Kunstwerke
- Architektonische Details
- Produktdesign-Elemente
Formeln zur regelmäßigen Pyramide
Mantelhöhe (s)
Mantelhöhe mit Kotangens-Beziehung für n-Eck
Kantenlänge (e)
Kantenlänge von Spitze zu Basis-Ecken
Grundfläche (A)
Fläche des regelmäßigen n-Ecks
Seitenfläche (As)
Fläche einer dreieckigen Seitenfläche
Mantelfläche (Am)
Summe aller n Seitenflächen
Oberfläche (S)
Grundfläche plus Mantelfläche
Umfang (P)
Umfang des regelmäßigen n-Ecks
Volumen (V)
Ein Drittel Grundfläche mal Höhe
Berechnungsbeispiel für eine regelmäßige Pyramide
Gegeben
Gesucht: Alle Eigenschaften der regelmäßigen fünfeckigen Pyramide
1. Grundfläche-Berechnung
Für n=5, a=8:
\[A = \frac{n \cdot a^2}{4 \cdot \tan(\frac{\pi}{n})}\] \[= \frac{5 \cdot 8^2}{4 \cdot \tan(\frac{\pi}{5})}\] \[= \frac{5 \cdot 64}{4 \cdot \tan(36°)}\] \[= \frac{320}{4 \cdot 0.7265} ≈ \frac{320}{2.906} ≈ 110.11\]Die Grundfläche beträgt etwa 110.11 Flächeneinheiten
2. Mantelhöhe-Berechnung
Mantelhöhe für n=5:
\[s = \sqrt{h^2 + \frac{a^2 \cdot \cot^2(\frac{\pi}{n})}{4}}\] \[= \sqrt{10^2 + \frac{8^2 \cdot \cot^2(36°)}{4}}\] \[= \sqrt{100 + \frac{64 \cdot 1.376^2}{4}}\] \[= \sqrt{100 + \frac{64 \cdot 1.894}{4}} ≈ \sqrt{100 + 30.3} ≈ 11.42\]Die Mantelhöhe beträgt etwa 11.42 Längeneinheiten
3. Kantenlänge-Berechnung
Kantenlänge von Spitze zu Ecken:
\[e = \sqrt{s^2 + \frac{a^2}{4}}\] \[= \sqrt{11.42^2 + \frac{8^2}{4}}\] \[= \sqrt{130.42 + \frac{64}{4}}\] \[= \sqrt{130.42 + 16} = \sqrt{146.42} ≈ 12.10\]Die Kantenlänge beträgt etwa 12.10 Längeneinheiten
4. Flächen-Berechnungen
Seiten- und Mantelfläche:
Seitenfläche: \(A_s = \frac{a \cdot s}{2} = \frac{8 \cdot 11.42}{2} ≈ 45.68\)Mantelfläche: \(A_m = n \cdot A_s = 5 \cdot 45.68 ≈ 228.4\)
Oberfläche: \(S = A + A_m = 110.11 + 228.4 ≈ 338.51\)
Seitenfläche: 45.68, Mantelfläche: 228.4, Oberfläche: 338.51
5. Volumen und Umfang
Volumen und Basis-Umfang:
Volumen: \(V = \frac{A \cdot h}{3} = \frac{110.11 \cdot 10}{3} ≈ 367.03\)Umfang: \(P = n \cdot a = 5 \cdot 8 = 40\)
Volumen: 367.03, Umfang: 40 Längeneinheiten
6. Die perfekte regelmäßige Pyramide
Die regelmäßige fünfeckige Pyramide mit perfekter Symmetrie
Die regelmäßige Pyramide: Universelle geometrische Perfektion
Die regelmäßige Pyramide ist die universellste und eleganteste Form aller Pyramiden. Mit einem regelmäßigen n-Eck als Basis vereint sie die Perfektion der ebenen Geometrie mit der räumlichen Struktur einer Pyramide. Diese geometrische Form ist ein Meisterwerk der Symmetrie, bei dem alle mathematischen Beziehungen durch trigonometrische Funktionen beschrieben werden. Die regelmäßige Pyramide ist nicht nur ein theoretisches Konzept, sondern findet praktische Anwendung in Architektur, Kristallographie und Design, wo perfekte Symmetrie und mathematische Eleganz gefragt sind.
Die Geometrie der universellen Symmetrie
Die regelmäßige Pyramide zeigt die Perfektion der n-fachen Symmetrie:
- Regelmäßige Basis: n-Eck mit gleichen Seiten und Winkeln für perfekte Symmetrie
- Kongruente Seitenflächen: Alle n Seitenflächen sind identische gleichschenklige Dreiecke
- n-fache Rotationssymmetrie: Unveränderlich bei Rotation um 360°/n
- Trigonometrische Beziehungen: Alle Parameter durch sin, cos, tan ausdrückbar
- Universelle Skalierbarkeit: Funktioniert für jedes n ≥ 3
- Zentrale Spitze: Optimale Kraftverteilung zur Basis
- Mathematische Eleganz: Perfekte Verbindung von 2D und 3D Geometrie
Trigonometrische Eleganz
n-Eck Grundfläche
Die Grundflächenformel A = na²/(4tan(π/n)) zeigt die elegante Beziehung zwischen der Eckenanzahl und der trigonometrischen Tangens-Funktion.
Mantelhöhen-Trigonometrie
Die Mantelhöhe verwendet den Kotangens, um die perfekte Beziehung zwischen Basis-Geometrie und Pyramiden-Höhe herzustellen.
Universelle Anwendbarkeit
Von n=3 (Dreieck) bis n→∞ (Kreis) funktionieren alle Formeln und zeigen die mathematische Schönheit der regelmäßigen Vielecke.
Symmetrie-Perfektion
Die n-fache Rotationssymmetrie macht diese Pyramide zum Inbegriff geometrischer Perfektion und struktureller Schönheit.
Zusammenfassung
Die regelmäßige Pyramide ist der Höhepunkt der Pyramiden-Geometrie. Ihre universelle Anwendbarkeit für jede Eckenanzahl n, kombiniert mit der eleganten trigonometrischen Beschreibung aller Parameter, macht sie zu einem Meisterwerk der Mathematik. Von der einfachsten Form (n=3, Dreieckspyramide) bis zu komplexen Vieleck-Pyramiden zeigt sie, wie mathematische Prinzipien zu praktischer Schönheit führen. Die regelmäßige Pyramide verbindet die Perfektion der ebenen Geometrie mit der räumlichen Eleganz der Pyramiden-Form und schafft dabei eine universelle geometrische Sprache. Ihre Bedeutung reicht von der reinen Mathematik über die Architektur bis hin zur Natur, wo sie als Grundprinzip für Kristalle, biologische Strukturen und technische Anwendungen dient. Sie ist damit nicht nur eine geometrische Form, sondern ein Symbol für die universelle Harmonie mathematischer Prinzipien.
|
|
|
|