Fünfeckige Doppelpyramide Rechner
Rechner und Formeln zur Berechnung einer regelmäßigen fünfeckigen Doppelpyramide
Pentagon Doppelpyramide Rechner
Die Regelmäßige Fünfeckige Doppelpyramide
Die fünfeckige Doppelpyramide ist eine Doppelpyramide mit regelmäßigem Pentagon als Basis, die den Goldenen Schnitt verkörpert.
Pentagon Doppelpyramide Eigenschaften
Der Goldene Schnitt in 3D: Zehn gleichschenklige Dreiecke um ein Pentagon
Pentagon Struktur
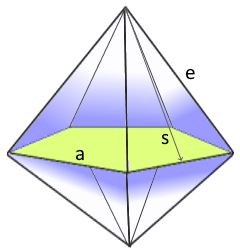
Die Pentagon-Doppelpyramide mit goldenem Schnitt.
Zehn gleichschenklige Dreiecke.
|
|
Was ist eine fünfeckige Doppelpyramide?
Die fünfeckige Doppelpyramide ist ein faszinierender geometrischer Körper:
- Definition: Zwei Pyramiden mit regelmäßigem Pentagon als gemeinsame Basis
- Struktur: 10 gleichschenklige Dreiecke als Seitenflächen
- Goldener Schnitt: Pentagon verkörpert den Goldenen Schnitt φ
- Ecken: 7 Ecken (5 äquatorial + 2 polar)
- Kanten: 15 Kanten (5 Pentagon + 10 Pyramidenkanten)
- Symmetrie: Fünfzählige Rotationssymmetrie
Geometrische Eigenschaften der Pentagon Doppelpyramide
Die fünfeckige Doppelpyramide zeigt bemerkenswerte geometrische Eigenschaften:
Grundparameter
- Flächen: 10 gleichschenklige Dreiecke
- Ecken: 7 Ecken (5+1+1)
- Kanten: 15 Kanten (5+5+5)
- Euler-Charakteristik: V - E + F = 7 - 15 + 10 = 2
Besondere Eigenschaften
- Pentagon-Basis: Regelmäßiges Fünfeck mit goldenem Schnitt
- Deltaeder: Alle Flächen sind Dreiecke
- Symmetrie: D₅ₕ-Symmetrie mit 5-zähliger Achse
- Konvex: Alle Kanten und Ecken ragen nach außen
Mathematische Beziehungen
Die fünfeckige Doppelpyramide folgt den Gesetzen des Goldenen Schnitts:
Pentagon-Mathematik
Verwendet Kotangens von 36° für Pentagon-Berechnungen.
Goldener Schnitt
Das Pentagon verkörpert den Goldenen Schnitt in der Geometrie.
Anwendungen der Pentagon Doppelpyramide
Fünfeckige Doppelpyramiden finden Anwendung in verschiedenen Bereichen:
Architektur & Design
- Moderne Gebäudespitzen
- Dekorative Elemente
- Pavillon-Konstruktionen
- Kunstinstallationen
Wissenschaft & Natur
- Kristallographische Formen
- Biologische Strukturen
- Molekulare Geometrie
- Optische Systeme
Bildung & Mathematik
- Goldener Schnitt Studien
- Pentagon-Geometrie
- 3D-Modellierung
- Symmetrie-Analysen
Kunst & Symbolik
- Geometrische Skulpturen
- Spirituelle Symbole
- Schmuckdesign
- Dekorative Objekte
Formeln zur fünfeckigen Doppelpyramide
Mantelhöhe (s)
Höhe der Seitenflächen mit Pentagon-Kotangens
Kantenlänge (e)
Länge der Pyramidenkanten
Gesamthöhe (i)
Doppelte Höhe einer Einzelpyramide
Eine Seitenfläche (As)
Fläche eines gleichschenkligen Dreiecks
Oberfläche (S)
Zehn Dreiecke: 5 × 2 × (a·s)/2
Umfang (P)
Umfang des regelmäßigen Pentagons
Volumen (V)
Pentagon-Fläche × Höh × 2/3 für Doppelpyramide
Berechnungsbeispiel für eine fünfeckige Doppelpyramide
Gegeben
Gesucht: Alle Eigenschaften der fünfeckigen Doppelpyramide
1. Mantelhöhe-Berechnung
Für a = 8, h = 10:
\[s = \sqrt{10^2 + \frac{8^2 \cdot \cot^2\left(\frac{\pi}{5}\right)}{4}}\] \[\cot\left(\frac{\pi}{5}\right) ≈ 1.376\] \[s = \sqrt{100 + \frac{64 \cdot 1.894}{4}} ≈ 12.1\]Die Mantelhöhe beträgt etwa 12.1 Längeneinheiten
2. Kantenlänge-Berechnung
Für s ≈ 12.1, a = 8:
\[e = \sqrt{\frac{12.1^2 + 8^2}{4}}\] \[e = \sqrt{\frac{146.41 + 64}{4}}\] \[e ≈ \sqrt{52.6} ≈ 7.25\]Die Kantenlänge beträgt etwa 7.25 Längeneinheiten
3. Gesamthöhe-Berechnung
Für h = 10:
\[i = 2 \cdot h\] \[i = 2 \cdot 10\] \[i = 20\]Die Gesamthöhe beträgt 20 Längeneinheiten
4. Oberfläche-Berechnung
Für a = 8, s ≈ 12.1:
\[S = 5 \cdot a \cdot s\] \[S = 5 \cdot 8 \cdot 12.1\] \[S = 484\]Die Oberfläche beträgt etwa 484 Flächeneinheiten
5. Umfang-Berechnung
Für a = 8:
\[P = 5 \cdot a\] \[P = 5 \cdot 8\] \[P = 40\]Der Umfang beträgt 40 Längeneinheiten
6. Volumen-Berechnung
Für a = 8, h = 10:
\[V = \frac{5 \cdot 8^2 \cdot 10}{6 \cdot \tan\left(\frac{\pi}{5}\right)}\] \[\tan\left(\frac{\pi}{5}\right) ≈ 0.726\] \[V ≈ \frac{3200}{4.356} ≈ 734.4\]Das Volumen beträgt etwa 734.4 Volumeneinheiten
Zusammenfassung der Ergebnisse
Die fünfeckige Doppelpyramide zeigt die Schönheit des Goldenen Schnitts in 3D
Die fünfeckige Doppelpyramide: Der Goldene Schnitt in 3D
Die fünfeckige Doppelpyramide ist ein außergewöhnlicher geometrischer Körper, der die Eleganz des Goldenen Schnitts in die dritte Dimension überträgt. Mit ihrem regelmäßigen Pentagon als Basis verkörpert sie die mathematische Perfektion, die seit der Antike Mathematiker und Künstler fasziniert. Die zehn gleichschenkligen Dreiecke, die ihre Oberfläche bilden, schaffen eine harmonische Struktur, die sowohl geometrische Schönheit als auch mathematische Tiefe vereint. Ihre Formeln mit Pentagon-spezifischen trigonometrischen Funktionen wie Kotangens von π/5 zeigen die enge Verbindung zum Goldenen Schnitt φ = (1+√5)/2.
Die Geometrie des Goldenen Schnitts
Die fünfeckige Doppelpyramide zeigt die Macht des Goldenen Schnitts in der Raumgeometrie:
- Pentagon-Basis: Regelmäßiges Fünfeck mit Goldenen-Schnitt-Proportionen
- D₅ₕ-Symmetrie: Fünfzählige Rotationssymmetrie mit Spiegelebene
- Deltaeder: Alle zehn Flächen sind gleichschenklige Dreiecke
- Goldene Proportionen: Seitenverhältnisse folgen φ-Beziehungen
- Harmonische Struktur: Perfekte Balance zwischen allen Komponenten
- Natürliche Form: Häufig in biologischen Strukturen anzutreffen
- Ästhetische Vollendung: Ideale Proportionen für Design und Kunst
Pentagon-Mathematik und Goldener Schnitt
Pentagon-Trigonometrie
Die Formeln verwenden spezielle trigonometrische Werte wie cot(π/5) ≈ 1.376, die direkt mit dem Goldenen Schnitt verbunden sind.
Goldene Verhältnisse
Das Pentagon verkörpert φ = (1+√5)/2 ≈ 1.618, den Goldenen Schnitt, der in vielen natürlichen Strukturen erscheint.
Doppelpyramide-Struktur
Zwei spiegelbildliche Pyramiden schaffen eine perfekt symmetrische Struktur mit zehn identischen Seitenflächen.
Natürliche Harmonie
Die Pentagon-Doppelpyramide zeigt, wie mathematische Perfektion und natürliche Schönheit miteinander verschmelzen.
Zusammenfassung
Die fünfeckige Doppelpyramide steht als Monument des Goldenen Schnitts in der dreidimensionalen Geometrie. Ihre Pentagon-Basis mit den charakteristischen φ-Proportionen, kombiniert mit zehn perfekt symmetrischen Dreiecksflächen, macht sie zu einem der ästhetisch ansprechendsten geometrischen Körper. Von der antiken Mathematik über die Renaissance-Kunst bis zur modernen Architektur bleibt sie ein faszinierendes Beispiel dafür, wie der Goldene Schnitt die Brücke zwischen Mathematik, Natur und Kunst schlägt. Ihre trigonometrischen Formeln mit Pentagon-spezifischen Werten zeigen die tiefe mathematische Struktur, die dieser scheinbar einfachen, aber außerordentlich eleganten Form zugrunde liegt. In der Welt der Geometrie verkörpert die fünfeckige Doppelpyramide die perfekte Synthese von mathematischer Präzision und natürlicher Harmonie.
|
|
|
|