Calculate Arrowhead Quadrilateral
Calculator and formulas for the arrowhead quadrilateral
Arrowhead Quadrilateral Calculator
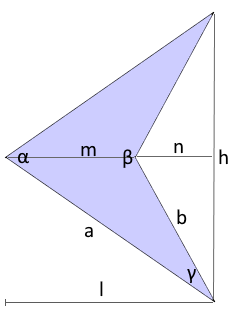
The Arrowhead Quadrilateral
An arrowhead quadrilateral has a characteristic arrow shape with perpendicular diagonals, with one diagonal lying outside the figure.
Arrowhead Quadrilateral Structure
Arrowhead properties
Key feature: Diagonals are perpendicular, one lies outside
The arrowhead quadrilateral with characteristic arrow shape.
Diagonals are perpendicular to each other.
|
|
The Arrowhead Quadrilateral: Geometric elegance of the arrow shape
The arrowhead quadrilateral is a fascinating geometric shape with unique properties:
- Arrow shape: Characteristic tip with symmetrical wings
- Perpendicular diagonals: Diagonals meet at right angles
- Exterior diagonal: One diagonal lies outside the figure
- Angle sum: α + β + 2γ = 360°
- Symmetry: Axial symmetry along the center line
- Special parameters: Inner length m and exterior length n
Special geometry of the arrowhead quadrilateral
The geometric properties of the arrowhead quadrilateral are unique:
Diagonal system
- Both diagonals are perpendicular
- One diagonal lies completely outside the figure
- Intersection point of diagonals as geometric center
- Special length ratios m and n
Angle properties
- Special angle sum: α + β + 2γ = 360°
- Angle γ occurs twice (symmetry)
- Trigonometric relations with half-angles
- Reflex angle possible (β > 180°)
Mathematical treatment of the arrowhead quadrilateral
The calculation of the arrowhead quadrilateral uses special trigonometric relations:
Sine relations
- a/b = sin(β/2) / sin(α/2)
- Half angles in the formulas
- Inner length m via sine ratio
- Exterior length n with a special formula
Area calculation
- Composed of several subareas
- A = (l·h)/2 - (n·h)/2
- Height h = 2·√(b² - n²)
- Pythagorean-based height formula
Applications of the arrowhead quadrilateral
Arrowhead quadrilaterals have many practical applications:
Navigation & signage
- Arrow symbols in traffic guidance systems
- Direction indicators in navigation
- Signposts and orientation aids
- User interface elements (buttons, icons)
Engineering & design
- Aerodynamic shapes (aircraft parts)
- Flow-optimized components
- Arrowheads and projectiles
- Architectural accents
Graphics & communication
- Logo design with directional symbolism
- Infographics and charts
- Presentation elements
- Corporate design with dynamics
Games & interaction
- Game UI and menu navigation
- Cursors and pointer shapes
- Game design for direction indicators
- Interactive controls
Formulas for the arrowhead quadrilateral
Side-length relation
Sine ratio with half angles
Angle relation
Special angle sum of the arrowhead quadrilateral
Inner length m
Length in the inner region of the arrow
Exterior length n
Exterior segment of the diagonal
Total length l
Sum of inner and exterior lengths
Height h
Height using a Pythagorean relation
Perimeter U
Sum of all four side lengths
Area A
Difference of large and small triangle
Worked example for an arrowhead quadrilateral
Given
Find: All parameters of the arrowhead quadrilateral
1. Compute angle γ
Angle-sum formula for arrowhead quadrilateral
2. Side length b
Sine ratio with half angles
3. Special lengths m and n
Inner length, exterior length, total length and height
4. Complete arrowhead quadrilateral
The complete arrowhead quadrilateral — elegant arrow shape with mathematical precision!
The Arrowhead Quadrilateral: Geometry of direction and motion
The arrowhead quadrilateral embodies, like no other geometric form, the principle of direction and purposeful motion. With its distinctive arrow tip and unique mathematical properties — especially the perpendicular diagonals and special angle sum — it represents dynamic geometry and is used in many applications from navigation to modern interface design.
The unique mathematics of the arrowhead quadrilateral
The arrowhead quadrilateral fascinates with its special mathematical properties:
- Perpendicular diagonals: Both diagonals are at right angles
- Exterior diagonal: One diagonal lies completely outside the figure
- Special angle sum: α + β + 2γ = 360°
- Half-angle trigonometry: Formulas use sin(α/2) and sin(β/2)
- Inner and exterior lengths: Special parameters m and n for the geometry
- Symmetry: Axial symmetry along the arrow's longitudinal axis
Arrowhead shapes in nature and culture
The arrow shape is deeply rooted in human culture and nature:
Natural arrow shapes
Many leaf shapes show arrow-like geometry. Plant spearheads and the body shapes of fish use similar aerodynamic principles.
Cultural symbolism
For millennia, arrows have symbolized direction, goals and progress. From prehistoric cave paintings to modern icons — the arrow shape is universally understood.
Technical evolution
From bow and arrow to rockets to digital cursors — the arrow shape has evolved technically, but its basic geometry has remained constant.
Psychological effect
Arrows guide the gaze and attention. They create visual tension and suggest movement, even in static depictions.
Modern applications in the digital world
The arrowhead quadrilateral gains new significance in the digital era:
- User interface design: Buttons, menu navigation and interactive elements
- Icon design: Arrows as universal symbols for direction and action
- Infographics: Visual guidance and data-flow representation
- Game design: Movement directions and targeting systems
- Architectural design: Dynamic building forms and guidance systems
- Corporate identity: Logos with direction and progress symbolism
Technical challenges and solutions
Calculating arrowhead quadrilaterals brings special mathematical challenges:
Trigonometric complexity
The use of half angles in formulas requires special care in numerical computation and domain checks.
Geometric validation
Not all combinations of sides and angles lead to constructible arrowhead quadrilaterals. Geometric consistency checks are essential.
Numerical stability
Computing √(b² - n²) can lead to numerical issues for unfavorable parameters. Robust algorithms are important.
Visualization algorithms
Correct rendering with the exterior diagonal requires special techniques in CAD and graphics software.
Future perspectives of arrow geometry
The arrowhead quadrilateral inspires modern innovations:
- Aerodynamics: Bio-inspired flow optimization for vehicles and aircraft
- Robotics: Arrow-based navigation and orientation for autonomous systems
- Augmented reality: 3D arrow overlays for spatial navigation
- Smart cities: Dynamic guidance systems with arrow-shaped display elements
- Material design: Arrow-structured metamaterials with directional properties
- AI interfaces: Intuitive human-machine communication with arrow symbols
Summary
The arrowhead quadrilateral stands as a geometric embodiment of direction, goals and motion. Its unique mathematical properties — from perpendicular diagonals to the special angle sum — make it a fascinating subject of geometric study. In our increasingly navigation-aware and interface-oriented world, the arrowhead quadrilateral gains new relevance: from user experience design to traffic guidance systems to AI-assisted orientation. It reminds us that geometry is not only abstract mathematics but also a universal language of communication and navigation. The arrowhead quadrilateral — elegant, functional and timeless — remains a powerful symbol of human determination and technological progress.
|
|
|
|