Pfeilviereck berechnen
Rechner und Formeln für das pfeilförmige Viereck
Pfeilviereck Rechner
Das Pfeilviereck
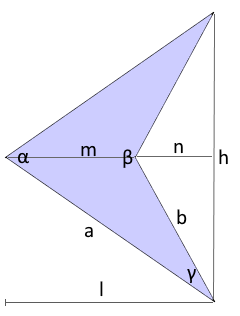
Ein Pfeilviereck hat eine charakteristische Pfeilform mit senkrechten Diagonalen, wobei eine Diagonale außerhalb liegt.
Pfeilviereck Struktur
Pfeilviereck Eigenschaften
Besonderheit: Diagonalen stehen senkrecht aufeinander, eine liegt außerhalb
Das Pfeilviereck mit charakteristischer Pfeilform.
Diagonalen stehen senkrecht aufeinander.
|
|
Das Pfeilviereck: Geometrische Eleganz der Pfeilform
Das Pfeilviereck ist eine faszinierende geometrische Form mit einzigartigen Eigenschaften:
- Pfeilform: Charakteristische Spitze mit symmetrischen Flügeln
- Senkrechte Diagonalen: Diagonalen stehen im rechten Winkel
- Außenliegende Diagonale: Eine Diagonale liegt außerhalb der Figur
- Winkelsumme: α + β + 2γ = 360°
- Symmetrie-Eigenschaften: Achsensymmetrisch zur Mittellinie
- Spezielle Parameter: Innenlänge m und Fehllänge n
Besondere Geometrie des Pfeilvierecks
Die geometrischen Eigenschaften des Pfeilvierecks sind einzigartig:
Diagonalen-System
- Beide Diagonalen stehen senkrecht aufeinander
- Eine Diagonale liegt komplett außerhalb der Figur
- Diagonalen-Schnittpunkt als geometrisches Zentrum
- Besondere Längen-Verhältnisse m und n
Winkel-Eigenschaften
- Spezielle Winkelsumme: α + β + 2γ = 360°
- Winkel γ tritt doppelt auf (Symmetrie)
- Trigonometrische Beziehungen mit halben Winkeln
- Reflex-Winkel möglich (β > 180°)
Mathematische Behandlung des Pfeilvierecks
Die Berechnung des Pfeilvierecks nutzt spezielle trigonometrische Beziehungen:
Sinus-Beziehungen
- a/b = sin(β/2) / sin(α/2)
- Halbe Winkel in den Formeln
- Innenlänge m über Sinus-Verhältnis
- Fehllänge n mit spezieller Formel
Flächenberechnung
- Zusammengesetzt aus mehreren Teilflächen
- A = (l·h)/2 - (n·h)/2
- Höhe h = 2·√(b² - n²)
- Pythagorean-basierte Höhen-Formel
Anwendungen des Pfeilvierecks
Pfeilvierecke finden vielfältige praktische Anwendungen:
Navigation & Zeichen
- Pfeilsymbole in Verkehrsleitsystemen
- Richtungsanzeiger in der Navigation
- Wegweiser und Orientierungshilfen
- User Interface Elemente (Buttons, Icons)
Technik & Design
- Aerodynamische Formen (Flugzeug-Teile)
- Strömungsoptimierte Bauteile
- Pfeilspitzen und Projektile
- Architektonische Akzente
Grafik & Kommunikation
- Logo-Design mit Richtungs-Symbolik
- Infografiken und Diagramme
- Präsentations-Elemente
- Corporate Design mit Dynamik
Spiele & Interaktion
- Spiel-Interface und Menü-Navigation
- Cursor und Zeiger-Formen
- Game-Design für Richtungsangaben
- Interaktive Bedienelemente
Formeln für das Pfeilviereck
Seitenlängen-Beziehung
Sinus-Verhältnis mit halben Winkeln
Winkel-Beziehung
Spezielle Winkelsumme des Pfeilvierecks
Innenlänge m
Länge im inneren Bereich des Pfeils
Fehllänge n
Außenliegende Länge der Diagonale
Gesamtlänge l
Summe aus Innenlänge und Fehllänge
Höhe h
Höhe mit Pythagoras-Beziehung
Umfang U
Summe aller vier Seitenlängen
Flächeninhalt A
Differenz aus großem und kleinem Dreieck
Rechenbeispiel für ein Pfeilviereck
Gegeben
Gesucht: Alle Parameter des Pfeilvierecks
1. Winkel γ berechnen
Winkelsumme-Formel für Pfeilviereck
2. Seitenlänge b
Sinus-Verhältnis mit halben Winkeln
3. Spezielle Längen m und n
Innenlänge, Fehllänge, Gesamtlänge und Höhe
4. Vollständiges Pfeilviereck
Das komplette Pfeilviereck - elegante Pfeilform mit mathematischer Präzision!
Das Pfeilviereck: Geometrie der Richtung und Bewegung
Das Pfeilviereck verkörpert wie keine andere geometrische Form das Prinzip der Richtung und zielgerichteten Bewegung. Mit seiner charakteristischen Pfeilspitze und den einzigartigen mathematischen Eigenschaften - insbesondere den senkrechten Diagonalen und der speziellen Winkelsumme - steht es für dynamische Geometrie und findet vielfältige Anwendungen von der Navigation bis zum modernen Interface-Design.
Die einzigartige Mathematik des Pfeilvierecks
Das Pfeilviereck fasziniert durch seine besonderen mathematischen Eigenschaften:
- Senkrechte Diagonalen: Beide Diagonalen stehen im rechten Winkel zueinander
- Außenliegende Diagonale: Eine Diagonale liegt komplett außerhalb der Figur
- Spezielle Winkelsumme: α + β + 2γ = 360° (statt der üblichen 360° für vier Winkel)
- Halbe-Winkel-Trigonometrie: Formeln verwenden sin(α/2) und sin(β/2)
- Innenlänge und Fehllänge: Spezielle Parameter m und n für die Geometrie
- Symmetrie-Eigenschaften: Achsensymmetrisch zur Längsachse des Pfeils
Pfeilvierecke in Natur und Kultur
Die Pfeilform ist tief in menschlicher Kultur und Natur verwurzelt:
Natürliche Pfeilformen
Viele Blattformen zeigen pfeilartige Geometrie. Speerspitzen von Pflanzen und die Körperform von Fischen nutzen ähnliche aerodynamische Prinzipien.
Kulturelle Symbolik
Seit Jahrtausenden symbolisieren Pfeile Richtung, Ziel und Fortschritt. Von steinzeitlichen Höhlenmalereien bis zu modernen Icons - die Pfeilform ist universell verständlich.
Technische Evolution
Von Pfeil und Bogen über Raketen bis zu digitalen Cursorn - die Pfeilform hat sich technisch weiterentwickelt, aber ihre Grundgeometrie blieb konstant.
Psychologische Wirkung
Pfeile lenken den Blick und die Aufmerksamkeit. Sie erzeugen visuelle Spannung und suggerieren Bewegung, selbst in statischen Darstellungen.
Moderne Anwendungen in der digitalen Welt
Das Pfeilviereck gewinnt in der digitalen Ära neue Bedeutung:
- User Interface Design: Buttons, Menü-Navigation und Interaktions-Elemente
- Icon-Design: Pfeile als universelle Symbole für Richtung und Aktion
- Infografik: Visuelle Führung und Datenfluss-Darstellung
- Game Design: Bewegungsrichtungen und Zielsysteme
- Architektonische Gestaltung: Dynamische Gebäude-Formen und Leitsysteme
- Corporate Identity: Logos mit Richtungs- und Fortschritts-Symbolik
Technische Herausforderungen und Lösungen
Die Berechnung von Pfeilvierecken bringt spezielle mathematische Herausforderungen mit sich:
Trigonometrische Komplexität
Die Verwendung halber Winkel in den Formeln erfordert besondere Aufmerksamkeit bei der numerischen Berechnung und Definitionsbereich-Prüfung.
Geometrische Validierung
Nicht alle Kombinationen von Seiten und Winkeln führen zu konstruierbaren Pfeilvierecken. Geometrische Konsistenz-Prüfungen sind essentiell.
Numerische Stabilität
Die Berechnung von √(b² - n²) kann bei ungünstigen Parametern zu numerischen Problemen führen. Robuste Algorithmen sind wichtig.
Visualisierungs-Algorithmen
Die korrekte Darstellung mit der außenliegenden Diagonale erfordert spezielle Rendering-Techniken in CAD- und Grafik-Software.
Zukunftsperspektiven der Pfeil-Geometrie
Das Pfeilviereck inspiriert moderne Innovationen:
- Aerodynamik: Bio-inspirierte Strömungsoptimierung für Fahrzeuge und Fluggeräte
- Robotik: Pfeil-basierte Navigation und Orientierung für autonome Systeme
- Augmented Reality: 3D-Pfeil-Overlays für räumliche Navigation
- Smart Cities: Dynamische Leitsysteme mit pfeilförmigen Display-Elementen
- Materialdesign: Pfeil-strukturierte Metamaterialien mit gerichteten Eigenschaften
- KI-Interface: Intuitive Mensch-Maschine-Kommunikation mit Pfeil-Symbolen
Zusammenfassung
Das Pfeilviereck steht als geometrische Verkörperung von Richtung, Ziel und Bewegung. Seine einzigartigen mathematischen Eigenschaften - von den senkrechten Diagonalen bis zur speziellen Winkelsumme - machen es zu einer faszinierenden Studienobjekt der Geometrie. In unserer zunehmend navigationsbewussten und interface-orientierten Welt gewinnt das Pfeilviereck neue Relevanz: von User-Experience-Design über Verkehrsleitsysteme bis hin zu KI-gestützten Orientierungshilfen. Es erinnert uns daran, dass Geometrie nicht nur abstrakte Mathematik ist, sondern eine universelle Sprache der Kommunikation und Navigation. Das Pfeilviereck - elegant, funktional und zeitlos - bleibt ein kraftvolles Symbol für menschliche Zielstrebigkeit und technischen Fortschritt.
|
|
|
|