Calculate Crossed Quadrilateral
Calculator for self-intersecting quadrilaterals
Crossed Quadrilateral Calculator
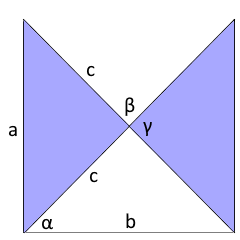
The crossed quadrilateral
A crossed quadrilateral is formed by the intersection of two side lines and shows self-intersection.
Crossed structure
Crossed properties
Self-intersecting: Two sides cross inside the shape
Crossed quadrilateral with intersection.
Two sides intersect inside the figure.
|
|
The crossed quadrilateral: geometry of self-intersection
The crossed quadrilateral is a fascinating form of non-convex geometry:
- Self-intersecting: Two side lines cross
- Non-convex: Interior regions fold
- Intersection angle: Determined by geometry
- Special leg: c = √(a²+b²)/2
- Simple area: A = (a×b)/2
- Angle relations: α = β/2
Special properties of the crossing
The geometric properties are shaped by the self-intersection:
Intersection geometry
- Two crossing side lines
- Intersection point inside the shape
- Creation of four subregions
- Overall non-convex shape
Angle system
- Intersection angle γ from cosine formula
- Supplement angle β = 180° - γ
- Half-angle α = β/2
- Symmetric angle relationships
Mathematics of the crossing
The mathematical relations are elegant despite the complexity:
Leg calculation
- c = √(a² + b²)/2
- Half-diagonal of the corresponding rectangle
- Pythagorean theorem applied
- Characteristic halving
Area formula
- A = (a × b)/2
- Half the rectangle area
- Simple multiplication
- Sign issues when crossing occurs
Applications of crossed shapes
Crossed quadrilaterals find surprising applications:
Mechanics & kinematics
- Joint connections with crossing
- Pantograph mechanisms
- Scissor-link systems
- Foldable mechanical structures
Design & art
- Geometric patterns and ornaments
- Op-art and visual illusions
- Architectural crossing elements
- Origami and folding techniques
Computer graphics
- Polygon triangulation
- Self-intersection detection
- 3D modeling algorithms
- Game engine collision systems
Mathematical research
- Topology of non-convex shapes
- Foundations of knot theory
- Algebraic geometry
- Differential geometry studies
Formulas for the crossed quadrilateral
Leg c
Half the rectangle diagonal
Area A
Half the rectangle area
Perimeter U
Twice base plus four times leg
Intersection angle γ
Angle at the intersection point
Angle relations
Supplement and half-angle relations
Worked example for a crossed quadrilateral
Given
Find: All parameters of the crossed quadrilateral
1. Compute leg
Half the diagonal of the corresponding rectangle
2. Area and perimeter
Half rectangle area and perimeter calculation
3. Angle calculations
Intersection angle and supplement
4. Complete crossed quadrilateral
Complete crossing geometry with characteristic angles!
The crossed quadrilateral: fascination of self-intersection
The crossed quadrilateral represents one of the most interesting forms of non-convex geometry. This self-intersecting structure arises from the crossing of two side lines and offers fascinating insights into complex geometric relationships. From mechanical applications to artistic design and mathematical research, the crossed quadrilateral shows how simple transformations can lead to surprisingly complex and beautiful shapes.
Mathematics of self-intersection
The crossed quadrilateral displays remarkable mathematical properties:
- Elegant leg formula: c = √(a²+b²)/2 — half the rectangle diagonal
- Simple area: A = (a×b)/2 — half the rectangle area
- Intersection angle: γ = arccos((2c²-a²)/(2c²))
- Angle hierarchy: α = β/2 and β = 180°-γ
- Topological complexity: Self-intersection creates four subregions
- Geometric duality: Convex input, non-convex output
Mechanical and technical applications
Crossed structures find diverse practical uses:
Kinematic systems
Pantographs and scissor-linkages use crossed geometries for motion transfer. These mechanisms enable precise scaling and force amplification.
Foldable structures
Folding tables, scissor lifts and collapsible frames rely on crossed principles. Self-intersection enables compact storage.
Robotics
Crossing joint connections in robot arms allow extended degrees of freedom. Parallelogram mechanisms with crossing optimize workspaces.
Textile industry
Weaving and knitting machines use crossed yarn paths. Crossing geometry is fundamental to textile manufacturing.
Art history and design
The aesthetic effect of crossed shapes is notable:
- Optical art: M.C. Escher and Op-Art used crossings for visual illusions
- Islamic ornamentation: Geometric patterns with crossed elements
- Gothic architecture: Crossing ribs and vault structures
- Modern sculpture: Minimal works with self-intersecting forms
- Logo design: Crossings as symbols of connection and integration
- Origami: Folding steps with crossed intermediate stages
Computer graphics and algorithmic challenges
Crossed quadrilaterals pose interesting problems for computer graphics:
Polygon processing
Self-intersection detection is a classic problem in computational geometry. Algorithms must efficiently find and handle intersection points.
Triangulation
Crossed polygons require special triangulation algorithms. Constrained Delaunay triangulation is often used.
Rendering
Crossed shapes can cause Z-buffer conflicts. Order-independent transparency is used as a solution.
Collision detection
Game engines must detect collisions with self-intersecting objects. Bounding volume hierarchies help with efficiency.
Mathematical research and topology
The crossed quadrilateral opens deep mathematical questions:
- Knot theory: Connections to mathematical knots and linkages
- Algebraic topology: Homology groups of self-intersecting shapes
- Differential geometry: Curvature behavior at intersection points
- Complex analysis: Riemann surfaces with branch points
- Combinatorial geometry: Counting problems for crossed configurations
- Optimization theory: Minimizing self-intersections in polygons
Summary
The crossed quadrilateral demonstrates the fascinating complexity that can arise from simple geometric transformations. By the self-intersection of two sides, a shape emerges that is both mathematically elegant and practically versatile. From the concise formulas c = √(a²+b²)/2 and A = (a×b)/2 to mechanical applications in pantographs and to artistic designs and computer graphics challenges, this form shows how geometry bridges theory and practice. The crossed quadrilateral reminds us that the beauty of mathematics often lies in unexpected turns. It symbolizes that complexity and simplicity, order and chaos, elegance and surprise can coexist harmoniously in the world of geometric forms.
|
|