Calculate frame
Calculator for rectangular frames with inner and outer dimensions
Frame calculator
Rectangular frame
A frame is a structural element with inner and outer dimensions.
Frame structure
Frame properties
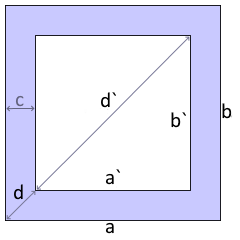
Structure: Inner and outer dimensions, material thickness c
Rectangular frame with thickness c.
Observe inner and outer dimensions.
The frame: structural elegance with functional geometry
The rectangular frame is a fundamental structural element:
- Material thickness c: Determines the frame width
- Outer dimensions: a × b (total size)
- Inner dimensions: a' × b' = (a-2c) × (b-2c)
- Frame area: A = a×b - a'×b' (material)
- Double perimeter: P = 2(a+b+a'+b')
- Diagonals: Outer d and inner d' differ
Geometric properties of the frame
The mathematical relations of the frame are precisely defined:
Dimension relations
- Inner length: a' = a - 2c
- Inner height: b' = b - 2c
- Material thickness c determines the difference
- Symmetric reduction by 2c
Area relations
- Frame area: A = a×b - a'×b'
- Inner area: A' = a'×b'
- Material vs. cavity share
- Calculable area efficiency
Mathematics of frame calculation
The algebraic relations of the frame are systematically built:
Linear transformations
- a' = a - 2c (linear reduction)
- b' = b - 2c (symmetric application)
- Constant thickness c for all sides
- Invertibility of the relations
Diagonal calculation
- Outer diagonal: d = √(a² + b²)
- Inner diagonal: d' = √(a'² + b'²)
- Pythagorean theorem applied
- Different diagonal lengths
Applications of frame structures
Frames find many practical applications:
Architecture & construction
- Window frames and door frames
- Structural frames for buildings
- Façade elements and cladding
- Balcony railings and barriers
Art & design
- Picture frames and matting
- Furniture design and shelving systems
- Decorative frame elements
- Interior design accents
Engineering & manufacturing
- Machine frames and chassis
- Electronics enclosures and cabinets
- Solar panel mounting systems
- Transport containers and crates
Digital & interface
- UI frames and border design
- Website layout and grid systems
- App interface elements
- Screen bezels and casings
Formulas for the frame
Inner dimensions
Reduction by twice the frame thickness
Diagonals
Pythagorean theorem for both diagonals
Perimeter P
Double sum of all edges
Frame area A
Outer area minus inner area
Inner area A'
Area of the inner cavity
Material efficiency
Ratio of inner to total area
Worked example for a frame
Given
Find: All parameters of the rectangular frame
1. Inner dimensions
Reduction by twice the frame thickness
2. Compute diagonals
Pythagorean theorem for both
3. Areas and perimeter
Area relations and perimeter
4. Complete frame
Complete frame with 80% material share!
The frame: structural geometry between inner and outer
The rectangular frame embodies the fundamental concept of structural delimitation in geometry. As an element that simultaneously defines inner and outer spaces, it unites practical functionality with mathematical elegance. From antique architectural elements to modern picture frames and digital interfaces - the frame structures our spatial and visual perception through precise geometric relations.
The mathematical essence of the frame
The frame illustrates fundamental geometric principles:
- Linear transformation: a' = a - 2c shows systematic dimension reduction
- Symmetric application: Same thickness c for all sides
- Area subtraction: A = A_outer - A_inner as basic principle
- Double geometry: Two concentric rectangles with defined relations
- Perimeter addition: P = 2(a+b+a'+b') accounts for both dimensions
- Diagonal variety: Different diagonal lengths for inner and outer
Structural significance in architecture and design
Frames play a central role in the built environment:
Architectural function
Window and door frames define openings, carry structural loads and create transitions between interior and exterior. Their sizing follows static and aesthetic principles.
Visual design
Picture frames guide the eye, create focus and establish visual hierarchies. The relation of frame width to picture size follows aesthetic proportions.
Technical construction
In engineering, frames serve as chassis, enclosures and mounting systems. Material efficiency and structural integrity determine optimal frame thicknesses.
Digital interfaces
UI frames structure screen content, create visual boundaries and direct user attention. Responsive design requires adaptive frame systems.
Optimization and efficiency of frame systems
Frame geometry enables systematic optimizations:
- Material efficiency: η = A'/(A+A') quantifies cavity share
- Structural optimization: Minimal frame thickness for maximal stability
- Manufacturing efficiency: Standardized profiles reduce costs
- Thermal consideration: Thermal bridges and insulation properties
- Aesthetic proportions: Golden ratio and harmonic relations
- Modular systems: Combinable frame elements for flexible use
Frames in modern technology
Contemporary applications expand the classic frame concept:
Solar technology
Photovoltaic modules require precise frame systems for mounting, sealing and electrical contact. Aluminum frames optimize weight and corrosion resistance.
Display technology
Modern screens minimize frames (bezels) for maximum display area. "Infinity displays" aim for bezel-less aesthetics.
Automotive design
Vehicle window frames combine aerodynamics with structural integrity. Lightweight design principles optimize frame geometry for weight reduction.
3D printing
Additive manufacturing enables complex frame structures with variable wall thicknesses and integrated functions.
Future perspectives of frame geometry
The development of intelligent and adaptive frame systems:
- Smart frames: Frames with integrated sensors and actuators
- Adaptive geometry: Variable thicknesses depending on load
- Sustainable materials: Bio-based and recyclable frame materials
- Digital integration: Frames with LED lighting and display functions
- AI-optimized designs: Machine learning for optimal proportions
- Nano-structuring: Microscopic frame systems in nanotechnology
Summary
The rectangular frame is an elegant example of functional geometry that connects inner and outer space through precise mathematical relations. The seemingly simple formulas a' = a - 2c and A = a×b - a'×b' hide deep principles of structural design and material efficiency. From antiquity to the modern era, the frame has structured our environment architecturally, artistically and technically. In a future of intelligent materials and adaptive systems, frame geometry remains a fundamental tool for shaping the interface between form and function, between enclosure and opening, and between the defined and the possible.
|
|