Rahmen berechnen
Rechner für rechteckige Rahmen mit Innen- und Außenmaßen
Rahmen Rechner
Rechteckiger Rahmen
Ein Rahmen ist ein strukturelles Element mit Innen- und Außendimensionen.
Rahmen Struktur
Rahmen Eigenschaften
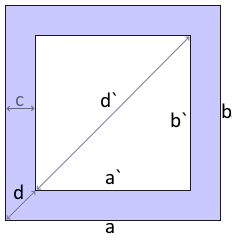
Struktur: Innen- und Außenabmessungen, Materialdicke c
Rechteckiger Rahmen mit Dicke c.
Innen- und Außendimensionen beachten.
|
|
Der Rahmen: Strukturelle Eleganz mit funktionaler Geometrie
Der rechteckige Rahmen ist ein fundamentales strukturelles Element:
- Materialdicke c: Bestimmt die Rahmenbreite
- Außenabmessungen: a × b (Gesamtmaße)
- Innenabmessungen: a' × b' = (a-2c) × (b-2c)
- Rahmenfläche: A = a×b - a'×b' (Material)
- Doppelter Umfang: P = 2(a+b+a'+b')
- Diagonalen: Außen d und Innen d' unterschiedlich
Geometrische Eigenschaften des Rahmens
Die mathematischen Beziehungen des Rahmens sind präzise definiert:
Dimensions-Beziehungen
- Innenlänge: a' = a - 2c
- Innenhöhe: b' = b - 2c
- Materialdicke c bestimmt Differenz
- Symmetrische Reduktion um 2c
Flächen-Beziehungen
- Rahmenfläche: A = a×b - a'×b'
- Innenfläche: A' = a'×b'
- Materialanteil vs. Hohlraum
- Flächeneffizienz berechenbar
Mathematik der Rahmen-Berechnung
Die algebraischen Beziehungen des Rahmens sind systematisch aufgebaut:
Lineare Transformationen
- a' = a - 2c (lineare Reduktion)
- b' = b - 2c (symmetrische Anwendung)
- Konstante Dicke c für alle Seiten
- Umkehrbarkeit der Beziehungen
Diagonalen-Berechnung
- Außen-Diagonale: d = √(a² + b²)
- Innen-Diagonale: d' = √(a'² + b'²)
- Pythagorischer Satz angewendet
- Verschiedene Diagonal-Längen
Anwendungen von Rahmen-Strukturen
Rahmen finden vielfältige praktische Anwendungen:
Architektur & Bauwesen
- Fensterrahmen und Türzargen
- Strukturelle Rahmen für Gebäude
- Fassaden-Elemente und Verkleidungen
- Balkon-Geländer und Absperrungen
Kunst & Design
- Bilderrahmen und Passepartouts
- Möbel-Design und Regal-Systeme
- Dekorative Rahmen-Elemente
- Interior Design Akzente
Technik & Fertigung
- Maschinenbau-Gestelle und Chassis
- Elektronik-Gehäuse und Schränke
- Solar-Panel-Montage-Systeme
- Transportbehälter und Container
Digital & Interface
- UI-Rahmen und Border-Design
- Website-Layout und Grid-Systeme
- App-Interface-Elemente
- Bildschirm-Bezels und Einfassungen
Formeln für den Rahmen
Innendimensionen
Reduktion um doppelte Rahmendicke
Diagonalen
Pythagorischer Satz für beide Diagonalen
Umfang P
Doppelte Summe aller Kanten
Rahmenfläche A
Außenfläche minus Innenfläche
Innenfläche A'
Fläche des Innenraums
Material-Effizienz
Verhältnis Innen- zu Gesamtfläche
Rechenbeispiel für einen Rahmen
Gegeben
Gesucht: Alle Parameter des rechteckigen Rahmens
1. Innendimensionen
Reduktion um doppelte Rahmendicke
2. Diagonalen berechnen
Pythagorischer Satz für beide
3. Flächen und Umfang
Flächenbeziehungen und Umfang
4. Vollständiger Rahmen
Kompletter Rahmen mit 80% Material-Anteil!
Der Rahmen: Strukturelle Geometrie zwischen Innen und Außen
Der rechteckige Rahmen verkörpert das fundamentale Konzept der strukturellen Abgrenzung in der Geometrie. Als Element, das gleichzeitig Innen- und Außenraum definiert, vereint er praktische Funktionalität mit mathematischer Eleganz. Von antiken Architekturelementen über moderne Bilderrahmen bis hin zu digitalen Interfaces - der Rahmen strukturiert unsere räumliche und visuelle Wahrnehmung durch präzise geometrische Beziehungen.
Die mathematische Essenz des Rahmens
Der Rahmen illustriert fundamentale geometrische Prinzipien:
- Lineare Transformation: a' = a - 2c zeigt systematische Dimensionsreduktion
- Symmetrische Anwendung: Gleiche Dicke c für alle Seiten
- Flächensubtraktion: A = A_außen - A_innen als Grundprinzip
- Doppelte Geometrie: Zwei konzentrische Rechtecke mit definierten Beziehungen
- Umfang-Addition: P = 2(a+b+a'+b') berücksichtigt beide Dimensionen
- Diagonal-Vielfalt: Verschiedene Diagonallängen für Innen- und Außenbereich
Strukturelle Bedeutung in Architektur und Design
Rahmen spielen eine zentrale Rolle in der gebauten Umwelt:
Architektonische Funktion
Fenster- und Türrahmen definieren Öffnungen, tragen strukturelle Lasten und schaffen Übergänge zwischen Innen- und Außenraum. Ihre Dimensionierung folgt statischen und ästhetischen Prinzipien.
Visuelle Gestaltung
Bilderrahmen lenken den Blick, schaffen Fokus und etablieren visuelle Hierarchien. Das Verhältnis von Rahmenbreite zu Bildgröße folgt ästhetischen Proportionsregeln.
Technische Konstruktion
In der Technik dienen Rahmen als Chassis, Gehäuse und Montagesysteme. Materialeffizienz und strukturelle Integrität bestimmen optimale Rahmendicken.
Digitale Interfaces
UI-Rahmen strukturieren Bildschirminhalte, schaffen visuelle Abgrenzungen und führen den Benutzerblick. Responsive Design erfordert adaptive Rahmensysteme.
Optimierung und Effizienz von Rahmen-Systemen
Die Rahmen-Geometrie ermöglicht systematische Optimierungen:
- Material-Effizienz: η = A'/(A+A') quantifiziert Hohlraum-Anteil
- Strukturelle Optimierung: Minimale Rahmendicke bei maximaler Stabilität
- Fertigungseffizienz: Standardisierte Rahmenprofile reduzieren Kosten
- Energetische Betrachtung: Wärmebrücken und Isolationseigenschaften
- Ästhetische Proportionen: Goldener Schnitt und harmonische Verhältnisse
- Modulare Systeme: Kombinierbare Rahmen-Elemente für flexible Anwendungen
Rahmen in der modernen Technologie
Zeitgenössische Anwendungen erweitern das klassische Rahmen-Konzept:
Solar-Technologie
Photovoltaik-Module benötigen präzise Rahmen-Systeme für Montage, Abdichtung und elektrische Kontaktierung. Aluminium-Rahmen optimieren Gewicht und Korrosionsresistenz.
Display-Technologie
Moderne Bildschirme minimieren Rahmen (Bezels) für maximale Bilddiagonale. "Infinity Displays" streben nach rahmenloser Ästhetik.
Automotive Design
Fahrzeug-Fensterrahmen verbinden Aerodynamik mit struktureller Integrität. Leichtbau-Prinzipien optimieren Rahmen-Geometrien für Gewichtsreduktion.
3D-Druck
Additive Fertigung ermöglicht komplexe Rahmen-Strukturen mit variablen Wandstärken und integrierten Funktionen.
Zukunftsperspektiven der Rahmen-Geometrie
Die Entwicklung intelligenter und adaptiver Rahmen-Systeme:
- Smart Frames: Rahmen mit integrierten Sensoren und Aktuatoren
- Adaptive Geometrie: Variable Rahmendicken je nach Belastung
- Nachhaltige Materialien: Bio-basierte und recycelbare Rahmen-Werkstoffe
- Digitale Integration: Rahmen mit LED-Beleuchtung und Display-Funktionen
- KI-optimierte Designs: Machine Learning für optimale Rahmen-Proportionen
- Nano-Strukturierung: Mikroskopische Rahmen-Systeme in der Nanotechnik
Zusammenfassung
Der rechteckige Rahmen steht als elegantes Beispiel für funktionale Geometrie, die Innen- und Außenraum durch präzise mathematische Beziehungen verbindet. Die scheinbar einfachen Formeln a' = a - 2c und A = a×b - a'×b' verbergen tiefe Prinzipien struktureller Gestaltung und Materialeffizienz. Von der Antike bis zur Moderne hat der Rahmen als architektonisches, künstlerisches und technisches Element unsere Umwelt strukturiert. In einer Zukunft intelligenter Materialien und adaptiver Systeme bleibt die Rahmen-Geometrie ein fundamentales Werkzeug für die Gestaltung der Schnittstelle zwischen Form und Funktion, zwischen Begrenzung und Öffnung, zwischen dem Definierten und dem Möglichen.
|
|
|
|