Konkaves Viereck berechnen
Rechner und Formeln für nach innen gewölbte Vierecke
Konkaves Viereck Rechner
Konkaves Viereck
Ein konkaves Viereck hat mindestens einen nach innen gewölbten Eckpunkt mit komplexer Geometrie und Diagonalen.
Konkaves Viereck
Konkave Viereck Eigenschaften
Besonderheit: Mindestens ein Innenwinkel > 180°, komplexe Diagonalen
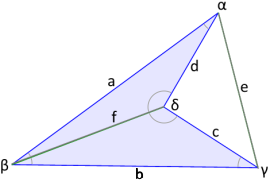
Das konkave Viereck mit nach innen gewölbtem Eckpunkt.
Eine Diagonale liegt außerhalb der Figur.
|
|
Das konkave Viereck: Nach innen gewölbte Geometrie
Ein konkaves Viereck unterscheidet sich fundamental von konvexen Vierecken:
- Konkav: "nach innen gewölbt" (lateinisch: concavus)
- Einspringender Eckpunkt: Mindestens ein Winkel > 180°
- Diagonalen-Problem: Eine Diagonale liegt außerhalb
- Komplexe Berechnung: Erfordert Dreiecks-Zerlegung
- Anwendungen: Architektur, Design, Technik
- Spezialfall: Nicht alle Formeln anwendbar
Geometrische Eigenschaften konkaver Vierecke
Die Geometrie konkaver Vierecke bringt besondere Herausforderungen mit sich:
Winkel-Eigenschaften
- Winkelsumme: α + β + γ + δ = 360°
- Mindestens ein Innenwinkel > 180°
- Reflexwinkel schaffen konkave Form
- Komplexe Winkel-Berechnungen nötig
Diagonalen-Verhalten
- Eine Diagonale liegt außerhalb der Figur
- Unterschiedliche Berechnungsmethoden
- Kosinussatz für Diagonalen e und f
- Hilfswinkelbereitung für Seite d
Berechnungs-Methodik für konkave Vierecke
Die mathematische Behandlung konkaver Vierecke erfordert spezielle Ansätze:
Dreiecks-Zerlegung
- Aufteilen in zwei Teildreiecke
- Kosinussatz für Diagonalen-Berechnung
- Hilfswinkel β₁ für komplexe Geometrie
- Heron'sche Formel für Teilflächen
Schrittweise Berechnung
- 1. Diagonalen e und f berechnen
- 2. Hilfswinkel β₁ bestimmen
- 3. Fehlende Seite d ermitteln
- 4. Restliche Winkel α und δ
Anwendungen konkaver Vierecke
Konkave Vierecke finden vielfältige praktische Anwendungen:
Architektur & Bauwesen
- Moderne Gebäude-Grundrisse
- Dachkonstruktionen mit Einsprüngen
- Innenhöfe und Gebäude-Nischen
- Fassaden-Gestaltung mit Rücksprüngen
Technik & Design
- Maschinenbau-Komponenten
- Platinen- und PCB-Design
- Automobilkarosserie-Teile
- Möbeldesign und Funktionalität
Gaming & Simulation
- Level-Design in Videospielen
- Polygon-Meshes in 3D-Modellierung
- Collision-Detection-Algorithmen
- Terrain-Generierung und Landschaften
Kunst & Medien
- Grafik-Design und Logo-Entwicklung
- Fotografie-Komposition
- Digitale Kunst und Animation
- UI/UX-Design für Apps
Formeln für das konkave Viereck
Diagonale e
Kosinussatz für Diagonale e
Diagonale f
Kosinussatz für Diagonale f
Hilfswinkel β₁
Für die Berechnung der Seite d
Seitenlänge d
Vierte Seite mit Hilfswinkel
Winkel α
Rückwärts-Berechnung mit Kosinussatz
Winkel δ
Winkelsumme im Viereck
Umfang U
Summe aller vier Seiten
Winkel β (Gamma)
Berechnung des Winkels zwischen den Seiten a und b
Flächeninhalt A (Heron)
mit \(s_1 = \frac{a+d+f}{2}\), \(s_2 = \frac{b+c+f}{2}\)
Heron'sche Formel für beide Teildreiecke
Rechenbeispiel für ein konkaves Viereck
Gegeben
Gesucht: Alle fehlenden Parameter des konkaven Vierecks
1. Diagonalen berechnen
Kosinussatz für beide Diagonalen
2. Hilfswinkel β₁
Benötigt für Seitenlänge d
3. Fehlende Seite und Winkel
Seite d und Winkel α mit den berechneten Werten
4. Vollständiges konkaves Viereck
Das komplette konkave Viereck - beachte den Reflexwinkel δ > 180°!
Das konkave Viereck: Herausforderung der nicht-konvexen Geometrie
Das konkave Viereck stellt eine der komplexeren Formen der Vierecks-Geometrie dar. Mit mindestens einem nach innen gewölbten Eckpunkt und der charakteristischen Eigenschaft, dass eine Diagonale außerhalb der Figur liegt, erfordert es spezielle mathematische Behandlungsmethoden und findet dennoch vielfältige Anwendungen in Technik, Architektur und Design.
Die Besonderheiten konkaver Geometrie
Konkave Vierecke unterscheiden sich fundamental von ihren konvexen Verwandten:
- Reflexwinkel: Mindestens ein Innenwinkel > 180° schafft die charakteristische Einbuchtung
- Diagonalen-Problem: Eine der beiden Diagonalen liegt außerhalb der Figur
- Komplexe Flächenberechnung: Zerlegung in Teildreiecke erforderlich
- Nicht-triviale Konstruktion: Standard-Viereck-Formeln nicht anwendbar
- Sichtlinien-Problematik: Nicht alle Punkte sind von allen anderen sichtbar
- Orientierung wichtig: Uhrzeigersinn vs. Gegenuhrzeigersinn beeinflusst Berechnungen
Mathematische Lösungsstrategien
Die Berechnung konkaver Vierecke erfordert clevere mathematische Ansätze:
Dreiecks-Zerlegung
Das konkave Viereck wird entlang einer Diagonale in zwei Dreiecke zerlegt, für die dann bekannte Formeln (Kosinussatz, Heron) angewandt werden können.
Schrittweise Berechnung
Zuerst werden die Diagonalen mit dem Kosinussatz berechnet, dann über Hilfwinkel die fehlende Seite ermittelt und schließlich alle Winkel bestimmt.
Winkel-Management
Der Umgang mit Winkeln > 180° erfordert besondere Aufmerksamkeit bei trigonometrischen Berechnungen und die richtige Interpretation der Arkusfunktionen.
Validierung wichtig
Die Ergebnisse müssen sorgfältig validiert werden, da nicht alle geometrisch sinnvoll konstruierbaren Vierecke auch mathematisch lösbar sind.
Anwendungen in der Praxis
Obwohl komplexer in der Berechnung, haben konkave Vierecke wichtige praktische Anwendungen:
- Architektur: Moderne Gebäude mit Einsprüngen, Innenhöfen und komplexen Grundrissen
- Industriedesign: Maschinenbauteile mit funktionalen Aussparungen und Nischen
- Computergrafik: Polygon-Rendering, Collision-Detection und räumliche Algorithmen
- Stadtplanung: Baublöcke mit Innenhöfen und verkehrstechnischen Einschnitten
- Möbeldesign: Ergonomische Formen und funktionale Einschnitte
- Elektronik: PCB-Layout mit Aussparungen für Komponenten
Herausforderungen und Grenzen
Die Arbeit mit konkaven Vierecken bringt spezielle Herausforderungen mit sich:
Berechnungs-Komplexität
Höhere mathematische Komplexität erfordert mehr Rechenschritte und größere Sorgfalt bei der numerischen Genauigkeit.
Konstruktions-Grenzen
Nicht alle Kombinationen von Seiten und Winkeln führen zu konstruierbaren konkaven Vierecken - geometrische Konsistenz ist entscheidend.
Software-Implementierung
CAD-Software und Berechnungsprogramme müssen spezielle Algorithmen für konkave Polygone implementieren.
Visualisierungs-Probleme
Die Darstellung und das Verständnis konkaver Formen ist schwieriger, da sie der intuitive Erwartung widersprechen können.
Konkave Geometrie in der digitalen Welt
In der digitalen Ära gewinnen konkave Vierecke neue Bedeutung:
- Game Development: Level-Design mit komplexen, nicht-konvexen Räumen
- 3D-Modellierung: Basis für komplexere konkave 3D-Körper
- Robotik: Pfadplanung um konkave Hindernisse herum
- Computer Vision: Objekterkennung und Formanalyse
- Finite Elemente: Diskretisierung komplexer Geometrien in der Simulation
- Künstliche Intelligenz: Räumliches Reasoning und Geometrie-Verständnis
Zusammenfassung
Das konkave Viereck steht als wichtiges Beispiel dafür, wie mathematische Komplexität und praktische Anwendung Hand in Hand gehen. Obwohl die Berechnung anspruchsvoller ist als bei konvexen Vierecken, eröffnet die konkave Geometrie neue Möglichkeiten in Design, Architektur und Technik. Die charakteristische "Einbuchtung" mit dem Reflexwinkel > 180° und der außenliegenden Diagonale erfordert spezielle mathematische Methoden, belohnt aber mit funktionalen und ästhetischen Vorteilen. In unserer zunehmend digitalen Welt, wo komplexe Geometrien in Computergrafik, Robotik und KI an Bedeutung gewinnen, bleibt das Verständnis konkaver Vierecke ein wertvoller Baustein für die Beherrschung nicht-konvexer geometrischer Strukturen.
|
|
|
|