Sehnenviereck berechnen
Rechner für Vierecke eingeschrieben in einen Kreis
Sehnenviereck Rechner
Das Sehnenviereck
Ein Sehnenviereck ist ein Viereck, dessen Eckpunkte auf einem Umkreis liegen. Alle Seiten sind Sehnen des Kreises.
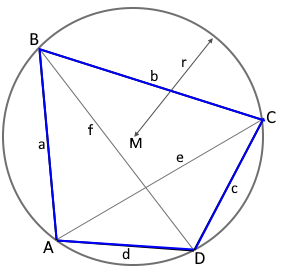
Sehnenviereck im Kreis
Sehnenviereck Eigenschaften
Ptolemäus-Theorem: e × f = a×c + b×d (Diagonalen-Beziehung)
Sehnenviereck eingeschrieben in Umkreis.
Alle Eckpunkte liegen auf der Kreislinie.
|
|
Das Sehnenviereck: Eingeschrieben in die Kreisperfektion
Das Sehnenviereck ist eine der elegantesten Formen der Geometrie:
- Umkreis-Eigenschaft: Alle Eckpunkte auf einem Kreis
- Sehnen-Seiten: Jede Seite ist eine Kreissehne
- Supplementäre Gegenwinkel: α + γ = β + δ = 180°
- Ptolemäus-Theorem: e × f = a×c + b×d
- Brahmagupta-Formel: A = √[(s-a)(s-b)(s-c)(s-d)]
- Eindeutige Bestimmung: Vier Seiten definieren alles
Besondere Eigenschaften des Sehnenvierecks
Die mathematischen Eigenschaften sind durch die Kreislage bestimmt:
Winkel-Eigenschaften
- Gegenüberliegende Winkel ergänzen zu 180°
- Umfangswinkel über gleichen Sehnen gleich
- Winkelsumme = 360° (wie alle Vierecke)
- Eindeutige Winkelbestimmung aus Seiten
Ptolemäus-Theorem
- Diagonalprodukt: e × f = a×c + b×d
- Fundamentalsatz für Sehnenvierecke
- Verallgemeinerung des Pythagorischen Satzes
- Basis für Diagonal-Berechnungen
Mathematik der Sehnenvierecks-Berechnung
Die mathematischen Beziehungen nutzen antike und moderne Erkenntnisse:
Brahmagupta-Formel (7. Jh.)
- A = √[(s-a)(s-b)(s-c)(s-d)]
- s = (a+b+c+d)/2 (Halbumfang)
- Verallgemeinerung der Heron-Formel
- Nur für Sehnenvierecke gültig
Ptolemäus-Beziehungen
- Diagonalen aus Seitenverhältnissen
- Komplexe Wurzelausdrücke
- Trigonometrische Winkelberechnungen
- Umkreisradius-Bestimmung
Anwendungen des Sehnenvierecks
Sehnenvierecke finden Anwendung in verschiedenen Bereichen:
Antike Astronomie
- Ptolemäus' astronomische Berechnungen
- Planetenbahn-Approximationen
- Kalender-Berechnungen
- Trigonometrische Tafeln
Geometrische Konstruktion
- Zirkel-und-Lineal-Konstruktionen
- Architektonische Planungen
- Gotische Fensterrosetten
- Symmetrische Ornamente
Moderne Technik
- Getriebe-Mechanismen
- Roboter-Kinematik
- CAD-System Algorithmen
- Computergrafik-Berechnungen
Wissenschaft
- Kristallographie-Analysen
- Molekül-Geometrie
- Optik und Linsensysteme
- Geodäsie und Vermessung
Formeln für das Sehnenviereck
Diagonalen e und f
Komplexe Diagonalen-Formeln aus Ptolemäus-Theorem
Brahmagupta-Flächenformel
Halbumfang s und die berühmte Flächenformel
Umkreisradius r
Radius des Umkreises durch alle Eckpunkte
Umfang P
Einfache Summe aller Seitenlängen
Winkel-Beziehungen
Gegenwinkel ergänzen sich zu 180° (charakteristisch für Sehnenvierecke)
Rechenbeispiel für ein Sehnenviereck
Gegeben
Gesucht: Alle Parameter des Sehnenvierecks
1. Halbumfang und Fläche
Brahmagupta-Formel in Aktion
2. Diagonalen berechnen
Ptolemäus-basierte Diagonal-Berechnung
3. Umkreis und Winkel
Supplementäre Gegenwinkel bestätigt: α + γ = β + δ = 180°
4. Vollständiges Sehnenviereck
Vollständig bestimmtes Sehnenviereck mit allen antiken Theoremen erfüllt!
Das Sehnenviereck: Brücke zwischen Antike und Moderne
Das Sehnenviereck vereint als eingeschriebenes Viereck die Eleganz der Kreisgeometrie mit der Komplexität mehrseitiger Figuren. Diese bemerkenswerte geometrische Form verbindet antike mathematische Einsichten von Brahmagupta und Ptolemäus mit modernen Anwendungen in Technik und Wissenschaft. Als Viereck, dessen Eckpunkte alle auf einem Kreis liegen, verkörpert es die harmonische Verbindung zwischen der perfekten Kreisform und der praktischen Vielseitigkeit von Polygonen.
Die antiken Wurzeln des Sehnenvierecks
Die mathematische Erforschung von Sehnenvierecken reicht über 1400 Jahre zurück:
- Brahmagupta (628 n.Chr.): Entwickelte die berühmte Flächenformel für Sehnenvierecke
- Ptolemäus (2. Jh. n.Chr.): Formulierte das fundamentale Theorem über Diagonalen
- Supplementäre Eigenschaft: Gegenüberliegende Winkel ergänzen sich zu 180°
- Eindeutige Bestimmung: Vier Seitenlängen definieren das Sehnenviereck vollständig
- Maximale Fläche: Unter allen Vierecken mit gegebenen Seiten hat das Sehnenviereck maximale Fläche
- Umkreis-Existenz: Der eindeutige Umkreis durch alle vier Eckpunkte
Mathematische Tiefe und Eleganz
Das Sehnenviereck zeigt bemerkenswerte mathematische Schönheit:
Brahmagupta-Formel
A = √[(s-a)(s-b)(s-c)(s-d)] verallgemeinert die Heron-Formel für Dreiecke. Diese elegante Formel funktioniert nur für Sehnenvierecke und spiegelt deren besondere Eigenschaften wider.
Ptolemäus-Theorem
Das Diagonalprodukt e×f = ac + bd ist eine fundamentale Beziehung, die nur in Sehnenvierecken gilt. Sie verallgemeinert den Pythagorischen Satz für nicht-rechtwinklige Vierecke.
Winkel-Harmonie
Die Supplementarität gegenüberliegender Winkel (α + γ = 180°) ist charakteristisch und ermöglicht elegante trigonometrische Berechnungen.
Extremal-Eigenschaft
Unter allen Vierecken mit gegebenen Seitenlängen hat das Sehnenviereck die maximale Fläche - ein Optimierungsprinzip der Natur.
Anwendungen in der modernen Welt
Trotz seiner antiken Ursprünge findet das Sehnenviereck moderne Anwendungen:
- Robotik und Kinematik: Gelenkverbindungen und Bewegungsmechanismen
- Computer-Aided Design: Algorithmen für komplexe geometrische Konstruktionen
- Architektur: Gotische Fensterrosetten und symmetrische Ornamente
- Kristallographie: Analyse von Molekülstrukturen und Kristallgittern
- Optik: Linsensysteme und Spiegelanordnungen
- Geodäsie: Vermessungstechnik und Triangulation
Das Sehnenviereck in der mathematischen Forschung
Moderne mathematische Forschung erweitert unser Verständnis:
Komplexe Analysis
Sehnenvierecke in der komplexen Ebene zeigen faszinierende Eigenschaften bezüglich konformer Abbildungen und Möbius-Transformationen.
Algebraische Geometrie
Die Beziehungen zwischen Seiten, Diagonalen und Winkeln bilden algebraische Varietäten mit interessanten topologischen Eigenschaften.
Numerische Methoden
Moderne Computermethoden ermöglichen die Lösung komplexer Sehnenviereck-Probleme und die Visualisierung ihrer Eigenschaften.
Diskrete Geometrie
Sehnenvierecke auf diskreten Gittern und ihre Anwendungen in der Computergrafik und digitalen Bildverarbeitung.
Zukunftsperspektiven
Das Sehnenviereck bleibt relevant für zukünftige Entwicklungen:
- Quantum Geometry: Quantenmechanische Systeme mit zyklischen Symmetrien
- Machine Learning: Geometrische Deep Learning Architekturen
- Nanotechnologie: Molekulare Maschinen mit zyklischen Strukturen
- Virtual Reality: Immersive Umgebungen mit optimierten geometrischen Strukturen
- Biomechanik: Gelenkbewegungen und biologische Konstruktionen
- Sustainable Design: Optimale Strukturen für ressourcenschonende Konstruktionen
Zusammenfassung
Das Sehnenviereck steht als zeitlose Brücke zwischen der antiken Weisheit von Brahmagupta und Ptolemäus und den modernen Anforderungen von Technik und Wissenschaft. Diese eingeschriebene geometrische Form verkörpert mathematische Eleganz durch ihre supplementären Winkel, die Brahmagupta-Formel und das Ptolemäus-Theorem. Als Optimum unter allen Vierecken mit gegebenen Seitenlängen zeigt es, wie die Natur Effizienz und Schönheit vereint. Von gotischen Kathedralen über Roboter-Kinematik bis hin zu Quantengeometrie bleibt das Sehnenviereck ein fundamentales Werkzeug für das Verständnis zyklischer und optimaler Strukturen. Es erinnert uns daran, dass antike mathematische Einsichten zeitlos sind und auch in einer hochtechnologisierten Zukunft ihre Gültigkeit behalten.
|
|
|
|