Ellipsoid Volume Calculator
Calculator and formulas for precise calculation of ellipsoid volume
Ellipsoid Volume Calculator
The Ellipsoid Volume
The ellipsoid volume is calculated using an elegant formula with three semi-axes a, b and c.
Ellipsoid Volume Properties
The volume formula: Elegant and universally applicable
Ellipsoid Visualization
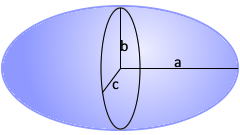
The ellipsoid with three semi-axes.
Volume easily calculable.
|
|
What is the ellipsoid volume?
The ellipsoid volume is a fundamental geometric measure:
- Definition: Space content of the three-dimensional ellipsoid
- Formula: Simple multiplication of the three semi-axes
- Universality: Applies to all ellipsoid types
- Precision: Exact mathematical calculation
- Application: From molecules to planets
- Elegance: Beautiful generalization of the sphere formula
Geometric foundations of ellipsoid volume
The ellipsoid volume is based on fundamental geometric principles:
Volume fundamentals
- Three semi-axes: a, b, c determine the shape
- Symmetry: Centrally symmetric body
- Scaling: Linear with each axis
- π-factor: Connection to circle geometry
Special properties
- Sphere generalization: Sphere as special case (a=b=c)
- Dimensional analysis: Cubic units
- Proportionality: Doubling one axis → double volume
- Universality: Same formula for all ellipsoid types
Mathematical aspects of volume calculation
The ellipsoid volume formula shows mathematical elegance:
Formula structure
Elegant generalization of the sphere formula. Exact and easy to calculate.
Mathematical properties
Triple integral over ellipsoid region. Coordinate transformation to sphere.
Applications of ellipsoid volume calculation
Ellipsoid volume calculations find diverse applications:
Natural Sciences
- Cell volume in biology
- Molecular volume in chemistry
- Particle volume in physics
- Droplet volume in fluid mechanics
Astronomy & Geophysics
- Planetary volumes
- Asteroid volumes
- Earth ellipsoid calculations
- Satellite orbit analysis
Engineering
- Container volumes
- Material quantity calculations
- CAD volume determination
- Manufacturing planning
Medicine & Biology
- Organ volumes
- Tumor volumes
- Cell size analysis
- Medical imaging
The Ellipsoid Volume Formula
Volume (V) - Main formula
The universal formula for any ellipsoid
Special case: Sphere (a = b = c = r)
The well-known sphere formula as special case
Ellipsoid of revolution (b = c)
Simplification for rotationally symmetric shapes
Dimensional analysis
Volume always has cubic length units
Derivation by integration
Transformation of the ellipsoid to unit sphere by coordinate substitution
Calculation example for ellipsoid volume
Given
Find: Volume of the ellipsoid with three different semi-axes
Step-by-step calculation
1. Insert formula:
\[V = \frac{4}{3} \cdot \pi \cdot a \cdot b \cdot c\]2. Insert values:
\[V = \frac{4}{3} \cdot \pi \cdot 8 \cdot 6 \cdot 4\]3. Calculate:
\[V = \frac{4}{3} \cdot \pi \cdot 192 = 256\pi\]4. Numerical result:
\[V ≈ 804.25 \text{ cm}^3\]The ellipsoid has a volume of approximately 804.25 cm³
Result analysis
Comparison with sphere:
Equivalent sphere:
\(r = \sqrt[3]{\frac{abc \cdot 4}{4}} = \sqrt[3]{192} ≈ 5.77 \text{ cm}\)
The ellipsoid corresponds to a sphere with radius ≈ 5.77 cm
Example: Sphere
\(V = \frac{4}{3}\pi \cdot 5^3 = \frac{500\pi}{3} ≈ 523.6 \text{ cm}^3\)
Example: Prolate
\(V = \frac{4}{3}\pi \cdot 10 \cdot 3^2 = 120\pi ≈ 377.0 \text{ cm}^3\)
Example: Oblate
\(V = \frac{4}{3}\pi \cdot 3 \cdot 7^2 = 196\pi ≈ 615.8 \text{ cm}^3\)
The Ellipsoid Volume: Elegance of three-dimensional geometry
The ellipsoid volume represents one of the most elegant formulas in three-dimensional geometry. With its simple structure V = (4/3)πabc, it generalizes the classical sphere formula to arbitrary ellipsoidal shapes and enables precise volume calculations for a variety of natural and technical objects. From biological cells to planetary bodies and industrial containers - the ellipsoid volume formula is a universal tool of applied mathematics.
The mathematical beauty of the volume formula
The ellipsoid volume shows the elegance of analytical geometry:
- Universal validity: One formula for all ellipsoid types
- Linear scaling: Doubling an axis doubles the volume
- Symmetric structure: All three semi-axes are equal in treatment
- π-connection: Elegant connection to circle geometry
- Integral derivation: Rigorous mathematical foundation
- Dimensional consistency: Cubic units as natural result
- Limit behavior: Natural transition to spheres and cylinders
Practical significance and applications
Scientific precision
The exact volume formula enables precise calculations in natural science and technology, from molecular chemistry to astronomy.
Universal applicability
From the smallest biological cell to the largest planet - the ellipsoid volume formula describes objects of all size scales.
Engineering relevance
In technology, the formula enables precise material calculations, manufacturing planning and quality control of ellipsoidal components.
Educational relevance
As a generalization of the sphere formula, it conveys deep understanding of three-dimensional geometry and integral calculus.
Summary
The ellipsoid volume formula V = (4/3)πabc embodies mathematical elegance in its purest form. Its simple structure hides the deep geometric insight that the volume of any ellipsoid is determined by the product of its three semi-axes and the universal factor (4/3)π. This formula combines theoretical beauty with practical applicability and shows how mathematics describes complex three-dimensional shapes with elementary operations. From basic research to industrial application, the ellipsoid volume remains a fundamental tool of applied geometry that bridges the gap between abstract mathematics and concrete reality.
|
|
|
|