Solid Angle Calculator
Calculator and formula for computing solid angles in steradian
Solid Angle Calculator
The Solid Angle
The solid angle is the ratio of the cut-out area to the square of the radius.
Solid Angle Properties
The solid angle: Three-dimensional extension of the planar angle
Solid Angle Visualization
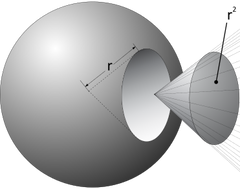
The Solid Angle
Three-dimensional angle measurement in steradian
Measure of the portion of a spherical surface.
Unit: Steradian (sr) - dimensionless.
|
|
What is a solid angle?
The solid angle is a fundamental geometric concept:
- Definition: Ratio of the spherical cap area to the square of the radius
- Unit: Steradian (sr) - dimensionless SI unit
- Analogy: Three-dimensional extension of the planar angle
- Full sphere: 4π steradian (≈ 12.57 sr)
- Half sphere: 2π steradian (≈ 6.28 sr)
- Applications: Optics, lighting, astronomy, physics
Geometric properties of the solid angle
The solid angle shows characteristic geometric properties:
Basic parameters
- Cap area A: Cut-out area on the spherical surface
- Sphere radius r: Radius of the reference sphere
- Solid angle Ω: Ω = A / r² (in steradian)
- Dimensionless: [sr] = [m²]/[m²] = dimensionless
Special properties
- Scale invariant: Ratio remains constant under scaling
- Additivity: Solid angles can be added
- Full-sphere reference: 4π sr for the entire sphere surface
- Conical projection: Corresponds to a cone from the center
Mathematical relations of the solid angle
The solid angle follows simple mathematical laws:
Basic formula
The solid angle is the ratio of the spherical cap area to the square of the radius.
Full-sphere reference
The entire spherical surface corresponds to a solid angle of 4π steradian.
Applications of the solid angle
Solid angles are applied in various fields:
Optics & Lighting
- Luminous intensity calculations
- Lighting engineering
- Light distribution
- Photometry
Astronomy & Astrophysics
- Observation of celestial objects
- Telescope fields of view
- Radiation distribution
- Satellite navigation
Physics & Engineering
- Radiation physics
- Nuclear physics
- Detector geometry
- Antenna engineering
Imaging & Computer Vision
- Camera fields of view
- 3D computer vision
- Image processing
- Robotics
Formulas for the solid angle
Solid angle (Ω)
Where A is the spherical cap area and r is the sphere radius. The solid angle is measured in steradian (sr).
Spherical cap area (A)
Area of the spherical cap from the solid angle
Sphere radius (r)
Radius from area and solid angle
Important solid angle values
4π sr ≈ 12.57 sr
2π sr ≈ 6.28 sr
π sr ≈ 3.14 sr
≈ 7.96% of the full sphere
Calculation examples for the solid angle
Example 1: Calculate solid angle
1. Solid angle calculation
For A = 50 cm², r = 10 cm:
\[\Omega = \frac{A}{r^2} = \frac{50}{10^2}\] \[\Omega = \frac{50}{100} = 0.5 \text{ sr}\]The solid angle is 0.5 steradian
2. Percentage of the full sphere
Fraction of the full sphere:
\[\text{Fraction} = \frac{\Omega}{4\pi} \times 100\%\] \[\text{Fraction} = \frac{0.5}{4\pi} \times 100\%\] \[\text{Fraction} ≈ 3.98\%\]The cap covers about 3.98% of the spherical surface
Example 2: Calculate spherical cap area
3. Spherical cap area calculation
For Ω = 1.0 sr, r = 8 cm:
\[A = \Omega \times r^2\] \[A = 1.0 \times 8^2\] \[A = 1.0 \times 64 = 64 \text{ cm}^2\]The spherical cap area is 64 cm²
4. Meaning of 1 steradian
1 sr corresponds to:
\[\frac{1 \text{ sr}}{4\pi \text{ sr}} = \frac{1}{4\pi} ≈ 7.96\%\]of the entire spherical surface
1 steradian is about 1/12.57 of the full sphere
Example 3: Calculate sphere radius
5. Radius calculation
For A = 100 cm², Ω = 0.8 sr:
\[r = \sqrt{\frac{A}{\Omega}} = \sqrt{\frac{100}{0.8}}\] \[r = \sqrt{125} ≈ 11.18 \text{ cm}\]The sphere radius is about 11.18 cm
6. Verification
Check:
\[\Omega = \frac{A}{r^2} = \frac{100}{11.18^2}\] \[\Omega = \frac{100}{125} = 0.8 \text{ sr} ✓\]The calculation is correct
7. Practical applications
Light cone calculations
Telescope fields of view
Lens acceptance angle
Radiation patterns
Solid angles are fundamental in many technical fields
The solid angle: Three-dimensional angle measurement
The solid angle is one of the most elegant and practically significant extensions of the classical angle concept into three dimensions. As the ratio of a spherical cap area to the square of the sphere radius, it represents a dimensionless quantity that is independent of the size of the reference sphere. This remarkable property makes it a universal tool in physics, engineering, and astronomy. From calculating luminous intensities in lighting engineering to characterizing telescope fields of view and describing radiation distributions, the solid angle demonstrates its fundamental importance for our understanding of three-dimensional geometry and physical phenomena.
The geometry of dimensionlessness
The solid angle shows the elegance of dimensionless geometry:
- Three-dimensional extension: Natural generalization of the planar angle
- Dimensionless: [A]/[r²] = [m²]/[m²] = dimensionless
- Scale invariance: Ratio remains constant under arbitrary scaling
- SI unit Steradian: Officially recognized, but derived unit
- Full-sphere normalization: 4π steradian for the entire spherical surface
- Geometric intuition: Conical projection from the center
- Additivity: Solid angles of adjacent regions add up
Scientific and technical significance
Optics and lighting
In photometry the solid angle describes the spread of light and enables precise calculations of illuminance.
Astronomy and astrophysics
Telescope fields of view, radiation distributions of stars and the characterization of astronomical instruments use solid angle concepts.
Radiation physics
The description of particle radiation, nuclear decays and detector geometries is fundamentally based on solid angle calculations.
Modern technologies
Computer vision, robotics and antenna engineering use solid angles for field-of-view analyses and radiation characteristics.
Summary
The solid angle embodies the perfect bridge between geometric abstraction and practical application. As a dimensionless quantity, it shows how mathematical concepts can gain universal validity independently of scales or specific units. Its simple definition Ω = A/r² hides a deep geometric truth: the shape of a spatial region can be characterized by the ratio of its projection. From quantifying light beams to describing telescope fields of view and characterizing modern sensor systems, the solid angle reveals its universal significance. It connects the purity of geometric concepts with the power of physical applications and remains a fundamental tool for understanding our three-dimensional world and the phenomena within it.
|
|
|
|