Triaxial Ellipsoid Calculator
Calculator and formulas for calculating volume and surface area of triaxial ellipsoids
Triaxial Ellipsoid Calculator
The Triaxial Ellipsoid
The triaxial ellipsoid is a three-axis body with three different semi-axes a, b and c.
Triaxial Ellipsoid Properties
The three-axis body: Three different semi-axes
Triaxial Ellipsoid
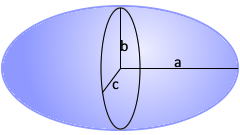
The most general ellipsoid with three axes.
Maximum geometric flexibility.
|
|
What is a triaxial ellipsoid?
The triaxial ellipsoid is the most general form of an ellipsoid:
- Definition: Ellipsoid with three different semi-axes
- Axes: a, b and c are all different
- Symmetry: No rotational symmetry
- Flexibility: Maximum geometric adaptability
- Complexity: Surface can only be calculated approximately
- Application: Crystals, molecules, astronomical objects
Geometric properties of the triaxial ellipsoid
The triaxial ellipsoid shows unique geometric properties:
Basic parameters
- Semi-axes: a, b, c (all different)
- Principal sections: Three different ellipses
- Symmetry planes: Three orthogonal planes
- Center symmetry: Point symmetry to the center
Special properties
- Complex curvature: Varies in all directions
- Elliptical cross-sections: All sections are ellipses
- Maximum flexibility: Adaptation to arbitrary shapes
- No rotational symmetry: Most general ellipsoid type
Mathematical relationships
The triaxial ellipsoid follows complex mathematical laws:
Volume formula
Simple formula with three semi-axes. Elegant and precise.
Surface formula
Knud Thomsen approximation. Maximum error: 1.061%.
Applications of the triaxial ellipsoid
Triaxial ellipsoids are used in various fields:
Crystallography
- Crystal structures
- Mineralogy
- Lattice parameters
- Anisotropic properties
Astronomy
- Asteroid shapes
- Irregular celestial bodies
- Galaxy modeling
- Gravitational fields
Molecular physics
- Molecular geometry
- Electron density distribution
- Vibrational ellipsoids
- Anisotropic tensors
Engineering & Design
- CAD modeling
- 3D objects
- Shape optimization
- Materials science
Formulas for the triaxial ellipsoid
Volume (V)
Exact formula for the volume
Surface area (S) - Approximation
Knud Thomsen approximation formula
Parameter p
Optimal exponent for minimal error
Accuracy
Very high accuracy for practical applications
Ellipsoid equation
Standard form of the triaxial ellipsoid equation in the coordinate system
Calculation example for a triaxial ellipsoid
Given
Find: Volume and surface area of the triaxial ellipsoid
2. Surface area calculation (approximation)
With p = 1.6075:
\[a^p = 6^{1.6075} ≈ 13.86\] \[b^p = 4^{1.6075} ≈ 7.73\] \[c^p = 3^{1.6075} ≈ 5.29\] \[S ≈ 4\pi \left( \frac{13.86 \cdot 7.73 + 13.86 \cdot 5.29 + 7.73 \cdot 5.29}{3} \right)^{1/1.6075}\] \[S ≈ 226.24 \text{ cm}^2\]The surface area is approximately 226.24 cm²
1. Volume calculation
For a = 6, b = 4, c = 3:
\[V = \frac{4}{3} \cdot \pi \cdot 6 \cdot 4 \cdot 3\] \[V = \frac{4}{3} \cdot \pi \cdot 72\] \[V = 96\pi\] \[V ≈ 301.59 \text{ cm}^3\]The volume is approximately 301.59 cm³
3. Ellipsoid analysis
Ratios of the axes:
\[\frac{a}{b} = \frac{6}{4} = 1.5\] \[\frac{a}{c} = \frac{6}{3} = 2.0\] \[\frac{b}{c} = \frac{4}{3} ≈ 1.33\]All axes different → triaxial
Typical triaxial ellipsoid with three different axes
4. The triaxial ellipsoid
The most general ellipsoid with three different axes
The triaxial ellipsoid: Highest geometric flexibility
The triaxial ellipsoid is the most general form of an ellipsoid and embodies maximum geometric flexibility. With three different semi-axes a, b and c, it can take on almost any ellipsoidal shape and therefore finds broad application in science and technology. While the volume can be calculated exactly, the surface calculation requires sophisticated approximation methods such as the elegant Knud Thomsen formula, which delivers practically exact results with minimal deviation.
The geometry of three axes
The triaxial ellipsoid shows the complexity and beauty of three-dimensional geometry:
- Three principal axes: a, b and c are all different and orthogonal
- No rotational symmetry: No ellipsoid of revolution possible
- Three symmetry planes: Orthogonal mirror planes through the center
- Elliptical cross-sections: Every section through the center is an ellipse
- Complex curvature: Curvature varies in all spatial directions
- Maximum adaptation: Optimal adaptation to arbitrary shapes
- Universal application: From molecules to galaxies
Mathematical complexity and elegance
Volume simplicity
Despite the geometric complexity, the volume formula is elegantly simple - the product of all three semi-axes with the π factor.
Surface challenge
The surface calculation requires elliptic integrals. Knud Thomsen's approximation formula offers a brilliant practical solution.
Scientific precision
With less than 1.1% deviation, the approximation formula enables precise calculations for all practical applications.
Universal significance
As the most general ellipsoid form, the triaxial ellipsoid is fundamental for describing complex three-dimensional objects.
Summary
The triaxial ellipsoid represents the completion of ellipsoid geometry through its three different semi-axes and the resulting maximum shape flexibility. Its elegant volume formula contrasts with the complex surface calculation, which becomes practically solvable through Knud Thomsen's ingenious approximation formula. From crystallography to astronomy to molecular physics, the triaxial ellipsoid enables the precise description of the most complex three-dimensional structures. As a universal tool of geometric modeling, it combines mathematical elegance with practical applicability and shows how the combination of three simple parameters can lead to infinite geometric diversity.
|
|
|
|