Spherical Cap Calculator
Calculator and formulas for calculating a spherical cap (spherical segment, dome)
Spherical Cap Calculator
The Spherical Cap
The spherical cap is a portion of a sphere cut off by a plane with a dome-shaped form.
Spherical Cap Properties
The spherical cap: Dome-shaped portion of a sphere
Spherical Cap Visualization
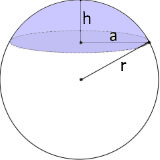
The Spherical Cap
Dome-shaped sphere section
Classic dome geometry.
Foundation for architecture and design.
|
|
What is a spherical cap?
The spherical cap is a fundamental geometric shape:
- Definition: Portion of a sphere cut off by a plane
- Shape: Dome-shaped form with flat base
- Spherical cap: The curved part of the surface
- Special case: Hemisphere is a special spherical cap
- Application: Architecture, domes, design
- Feature: Combines curved and flat surfaces
Geometric properties of the spherical cap
The spherical cap shows characteristic geometric properties:
Basic parameters
- Sphere radius r: Radius of the original complete sphere
- Cap height h: Height of the dome-shaped section
- Cap radius a: Radius of the circular base
- Cutting plane: Defines the separation position
Special properties
- Dome shape: Naturally stable and aesthetically pleasing form
- Hybrid surface: Curved cap plus flat base
- Scalability: From shallow cap to hemisphere
- Symmetry: Rotationally symmetric around central axis
Mathematical relationships of the spherical cap
The spherical cap follows elegant mathematical laws:
Volume formula
The volume grows quadratically with height. Accounts for the curvature of the original sphere.
Surface area formula
The surface area consists of curved cap and flat base area.
Applications of the spherical cap
Spherical caps find applications in various fields:
Architecture & Construction
- Dome constructions
- Churches and mosques
- Modern architecture
- Planetariums
Engineering
- Pressure vessel heads
- Tank covers
- Pipeline caps
- Mechanical engineering
Design & Art
- Product design
- Sculptural elements
- Furniture design
- Decorative objects
Science & Nature
- Geodesy
- Optics (lenses)
- Biology (cell shapes)
- Astronomy
Formulas for the spherical cap
Cap Volume (Vs)
Volume of the dome-shaped cap
Cap Height (h)
Height from sphere and cap radius
Cap Radius (a)
Radius of the circular base
Cap Surface Area (Sc)
Curved surface area of the spherical cap
Base Area (A)
Circular base area of the cap
Total Surface Area (S)
Cap plus base area
Calculation example for a spherical cap
Given
Find: All parameters of the spherical cap
1. Cap radius calculation
For r = 10 cm, h = 4 cm:
\[a = \sqrt{r^2 - (r - h)^2}\] \[a = \sqrt{100 - (10 - 4)^2}\] \[a = \sqrt{100 - 36} = \sqrt{64} = 8 \text{ cm}\]The cap radius is 8 cm
2. Volume calculation
With r = 10 cm, h = 4 cm:
\[V_s = \frac{π \cdot h^2}{3} \cdot (3r - h)\] \[V_s = \frac{π \cdot 16}{3} \cdot (30 - 4)\] \[V_s = \frac{16π \cdot 26}{3} ≈ 435.6 \text{ cm}^3\]The cap volume is approximately 435.6 cm³
3. Base area calculation
With a = 8 cm:
\[A = π \cdot a^2 = π \cdot 64\] \[A ≈ 201.06 \text{ cm}^2\]The base area is approximately 201.06 cm²
4. Cap surface calculation
With r = 10 cm, h = 4 cm:
\[S_c = 2πrh = 2π \cdot 10 \cdot 4\] \[S_c = 80π ≈ 251.33 \text{ cm}^2\]The cap surface is approximately 251.33 cm²
5. Total surface calculation
Cap plus base:
\[S = S_c + A\] \[S = 251.33 + 201.06\] \[S ≈ 452.39 \text{ cm}^2\]The total surface area is approximately 452.39 cm²
6. Summary
The spherical cap with 4 cm height
7. Comparison with hemisphere
V = 435.6 cm³
V = 2094.4 cm³
≈ 20.8%
The cap has about 1/5 the volume of a hemisphere
8. Geometric analysis
h/r = 4/10 = 0.4
a/r = 8/10 = 0.8
Shallow cap
Slightly curved
With h/r = 0.4, a relatively shallow spherical cap is formed
The Spherical Cap: Classic dome geometry
The spherical cap is one of the most fundamental and aesthetically appealing geometric shapes in mathematics. As a dome-shaped section of a sphere, it combines the natural elegance of spherical curvature with the practical functionality of a flat base. Its mathematical properties - from the quadratic height dependence of volume to the linear relationship between cap surface and height - make it an ideal example of the beauty of geometric relationships. The spherical cap is the foundation of countless architectural masterpieces and technical solutions.
The geometry of the dome
The spherical cap shows the perfection of dome-shaped geometry:
- Dome shape: Naturally stable and aesthetically pleasing form
- Flat base: Practical foundation surface for constructions
- Spherical cap: Curved surface with optimal stress distribution
- Scalable geometry: From shallow cap to hemisphere
- Rotational symmetry: Perfect symmetry around the vertical axis
- Mathematical elegance: Simple relationships between parameters
- Universal application: From architecture to engineering
Mathematical beauty
Volume elegance
The volume formula V = πh²(3r-h)/3 shows the quadratic dependence on height and elegant consideration of sphere curvature.
Surface harmony
The cap surface S = 2πrh is linearly proportional to height, leading to harmonious size relationships.
Architectural perfection
Domes from spherical caps offer optimal statics, natural acoustics and timeless aesthetic appeal.
Technical excellence
In technology, spherical caps enable optimal pressure distribution in vessels and pipelines.
Summary
The spherical cap embodies the perfect synthesis between mathematical elegance and practical functionality. As a dome-shaped section of a sphere, it shows the natural beauty of curved geometry and the constructive clarity of flat base surfaces. Its mathematical properties - from the quadratic height dependence of volume to the linear cap surface - demonstrate the harmonic relationships of spherical geometry. From the majestic domes of historic buildings to modern architectural masterpieces to technical applications in mechanical engineering and process technology, the spherical cap shows its universal significance. It connects the purity of geometric forms with the functionality of practical applications and remains a timeless symbol for the unity of beauty and utility in geometry.
|
|
|
|