Spherical Shell Calculator
Calculator and formulas for calculating a spherical shell
Spherical Shell Calculator
The Spherical Shell
The spherical shell (also called hollow sphere) is created by a spherical cavity in a larger sphere.
Spherical Shell Properties
The spherical shell: Hollow space with constant wall thickness
Spherical Shell Visualization
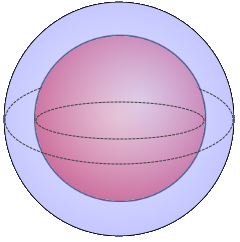
The Spherical Shell
Hollow sphere with constant wall thickness
Optimal material distribution for hollow spheres.
Light but stable.
|
|
What is a spherical shell?
The spherical shell is a special geometric shape:
- Definition: Hollow sphere with spherical cavity inside
- Structure: Large sphere minus smaller concentric sphere
- Wall thickness: Constant thickness a = R - r
- Material efficiency: Maximum stability with minimal material
- Application: Pressure vessels, ball bearings, architecture
- Feature: Double surface calculation (inside + outside)
Geometric properties of the spherical shell
The spherical shell shows unique geometric properties:
Basic parameters
- Outer radius R: Radius of the outer sphere surface
- Inner radius r: Radius of the spherical cavity
- Shell thickness a: Wall thickness a = R - r
- Concentricity: Both spheres have the same center
Special properties
- Double surface: Outer plus inner surface
- Material efficiency: Optimal stability/weight ratio
- Scalability: From thin shell to thick wall
- Symmetry: Complete spherical symmetry
Mathematical relationships of the spherical shell
The spherical shell follows elegant mathematical laws:
Volume formula
The shell volume as difference of two spheres. Elegant cubic difference formula.
Surface area formula
The total surface as sum of both sphere surfaces. Inner plus outer surface.
Applications of the spherical shell
Spherical shells find applications in various fields:
Mechanical Engineering & Technology
- Pressure vessels and tanks
- Ball bearings (hollow spheres)
- Lightweight constructions
- Precision mechanics
Aerospace & Aviation
- Satellite tanks
- Pressure cabins
- Lightweight structures
- Fuel tanks
Architecture & Construction
- Dome constructions
- Modern architecture
- Sculptural elements
- Lightweight roofs
Science & Research
- High-pressure experiments
- Materials research
- Physical models
- Biomechanics
Formulas for the spherical shell
Shell Thickness (a)
Difference between outer and inner radius
Shell Volume (V)
Difference of sphere volumes
Surface Area (S)
Sum of outer and inner surfaces
Individual Surfaces
Outer and inner surfaces separately
Geometric relationships
\(R > r > 0\)
\(a = R - r\)
Optimal with thin walls
The outer radius must be larger than the inner radius
Calculation example for a spherical shell
Given
Find: All parameters of the spherical shell
1. Shell thickness calculation
For R = 10 cm, r = 7 cm:
\[a = R - r = 10 - 7\] \[a = 3 \text{ cm}\]The shell thickness is 3 cm
2. Volume calculation
With R = 10 cm, r = 7 cm:
\[V = \frac{4π}{3} \cdot (R^3 - r^3)\] \[V = \frac{4π}{3} \cdot (1000 - 343)\] \[V = \frac{4π}{3} \cdot 657 ≈ 2753.8 \text{ cm}^3\]The shell volume is approximately 2753.8 cm³
3. Surface area calculation
With R = 10 cm, r = 7 cm:
\[S = 4π \cdot (R^2 + r^2)\] \[S = 4π \cdot (100 + 49)\] \[S = 4π \cdot 149 ≈ 1870.8 \text{ cm}^2\]The total surface area is approximately 1870.8 cm²
4. Individual surfaces
Split by inner/outer:
\[S_{outer} = 4π \cdot 10^2 = 400π ≈ 1256.6 \text{ cm}^2\] \[S_{inner} = 4π \cdot 7^2 = 196π ≈ 615.8 \text{ cm}^2\]Outer surface: 1256.6 cm², Inner surface: 615.8 cm²
5. Summary
The spherical shell with 3 cm wall thickness
6. Comparison with solid sphere
V = 2753.8 cm³
V = 4188.8 cm³
The hollow sphere saves about 1/3 material
7. Material efficiency analysis
a/R = 3/10 = 0.3
r³/R³ = 34.3%
Medium wall thickness
Very good balance
Optimal balance between stability and material savings
The Spherical Shell: Material efficiency through geometry
The spherical shell is a fascinating geometric shape that combines the elegance of sphere geometry with the principles of material efficiency. As a hollow sphere with constant wall thickness, it shows how maximum stability can be achieved with minimal material use through clever geometric design. The mathematical beauty lies in the elegant difference formulas for volume (R³-r³) and sum formulas for surfaces (R²+r²), which perfectly describe the essence of the hollow sphere.
The geometry of efficiency
The spherical shell shows the perfection of material-saving geometry:
- Double surface: Inner and outer surfaces for maximum functionality
- Constant wall thickness: Uniform material distribution and stability
- Spherical symmetry: Optimal pressure distribution in all directions
- Material efficiency: Maximum stability with minimal weight
- Scalability: From thin shells to thick walls
- Elegant mathematics: Simple difference and sum formulas
- Universal application: From microtechnology to large containers
Mathematical elegance
Difference formulas
The volume formula V = 4π/3 × (R³-r³) shows the elegant cubic difference that mathematically captures the essence of the hollow sphere.
Sum formulas
The surface formula S = 4π × (R²+r²) elegantly adds inner and outer surfaces to a total surface area.
Material optimization
The spherical shell enables material savings of 20-80% compared to solid spheres while maintaining structural integrity.
Technical perfection
In pressure vessels, spherical tanks and lightweight construction, the spherical shell shows its technical superiority through optimal stress distribution.
Summary
The spherical shell embodies the perfect harmony between geometric elegance and technical efficiency. As a hollow sphere with constant wall thickness, it unites the natural perfection of the spherical form with the principles of intelligent material utilization. Its mathematical properties - with the elegant difference formulas for volume and sum formulas for surface area - make it a fundamental building block of modern engineering. From high-pressure vessels to aerospace tanks to architectural dome constructions, the spherical shell shows its universal applicability. It impressively demonstrates how geometric perfection and practical material efficiency lead to technical solutions that are both mathematically beautiful and engineering optimal.
|
|
|
|