Spherical Ring Calculator
Calculator and formulas for calculating a spherical ring
Spherical Ring Calculator
The Spherical Ring
The spherical ring is a solid sphere with a cylindrical bore through the center.
Spherical Ring Properties
The spherical ring: Combination of spherical and cylindrical geometry
Spherical Ring Visualization
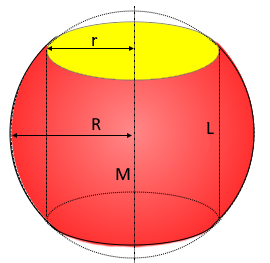
The Spherical Ring
Solid sphere with cylindrical bore
Combination of sphere and cylinder.
Curved outside, straight inside.
|
|
What is a spherical ring?
The spherical ring is a special geometric shape:
- Definition: Solid sphere with cylindrical bore through the center
- Outer surface: Symmetric spherical shell (spherical)
- Inner surface: Lateral surface of a straight circular cylinder
- Hybrid form: Combination of sphere and cylinder geometry
- Application: Technology, architecture, physics
- Feature: Complex surface area calculation
Geometric properties of the spherical ring
The spherical ring shows hybrid geometric properties:
Basic parameters
- Sphere radius R: Radius of the original solid sphere
- Cylinder radius r: Radius of the cylindrical bore
- Cylinder height L: Height of the bore (2√(R²-r²))
- Condition: r < R (bore must be smaller than sphere)
Special properties
- Hybrid surface: Spherical outside, cylindrical inside
- Complex volume: Dependent on L³ (not R³)
- Rotational symmetry: Around the axis of the bore
- Variable form: From thin ring to thick shell
Mathematical relationships of the spherical ring
The spherical ring follows complex mathematical laws:
Volume formula
The ring volume depends on L³. Surprisingly simple formula for complex geometry.
Surface area formula
The surface area considers both radii. Inner and outer surfaces combined.
Applications of the spherical ring
Spherical rings find applications in various fields:
Mechanical Engineering & Technology
- Bearings and bushings
- Hollow spheres with bores
- Fluid mechanics
- Precision mechanics
Physics & Chemistry
- Hollow sphere experiments
- Fluid mechanics
- Materials science
- Quantum mechanics
Architecture & Design
- Sculptural elements
- Modern architecture
- Product design
- Art objects
Mathematics & CAD
- Volume calculation
- CAD construction
- 3D modeling
- Finite elements
Formulas for the spherical ring
Cylinder height (L)
Height of the cylindrical bore
Ring volume (VR)
Volume of the spherical ring (without bore)
Cylinder volume (VC)
Volume of the cylindrical bore
Ring surface area (S)
Inner and outer surfaces combined
Geometric relationships
\(r < R\)
\(L_{max} = 2R\) (when r = 0)
\(L = 0\) (when r = R)
The cylinder radius must be smaller than the sphere radius
Calculation example for a spherical ring
Given
Find: All parameters of the spherical ring
1. Cylinder height calculation
For R = 8 cm, r = 6 cm:
\[L = 2 \cdot \sqrt{R^2 - r^2}\] \[L = 2 \cdot \sqrt{64 - 36} = 2 \cdot \sqrt{28}\] \[L = 2 \cdot 5.29 ≈ 10.58 \text{ cm}\]The cylinder height is approximately 10.58 cm
2. Ring volume calculation
With L ≈ 10.58 cm:
\[V_R = \frac{π \cdot L^3}{6}\] \[V_R = \frac{π \cdot (10.58)^3}{6}\] \[V_R = \frac{π \cdot 1184.5}{6} ≈ 620.03 \text{ cm}^3\]The ring volume is approximately 620.03 cm³
3. Cylinder volume calculation
With L ≈ 10.58 cm, r = 6 cm:
\[V_C = π \cdot L \cdot r^2\] \[V_C = π \cdot 10.58 \cdot 36\] \[V_C ≈ 1194.6 \text{ cm}^3\]The cylinder volume is approximately 1194.6 cm³
4. Ring surface calculation
With L ≈ 10.58 cm:
\[S = 2π \cdot L \cdot (r + R)\] \[S = 2π \cdot 10.58 \cdot (6 + 8)\] \[S = 2π \cdot 10.58 \cdot 14 ≈ 929.2 \text{ cm}^2\]The ring surface area is approximately 929.2 cm²
5. Summary
The spherical ring with R=8cm, r=6cm
6. Comparison with solid sphere
VR = 620.03 cm³
V = 2144.66 cm³
The ring has about 29% of the solid sphere volume
7. Geometric ratios
6/8 = 0.75
10.58/8 ≈ 1.32
R - r = 2 cm
Thick ring
With r/R = 0.75, a relatively thick spherical ring is formed
The Spherical Ring: Hybrid geometry of sphere and cylinder
The spherical ring is a fascinating geometric shape that combines the elegance of sphere geometry with the precision of cylindrical forms. As a solid sphere with a cylindrical bore through the center, it shows unique mathematical properties that make it interesting for both theoretical studies and practical applications. The spherical ring embodies the perfect synthesis between spherical outer shell and cylindrical inner structure, leading to surprisingly elegant formulas.
The geometry of the hybrid form
The spherical ring shows the fascination of geometric combinations:
- Spherical outer shell: Preservation of the original sphere surface
- Cylindrical bore: Straight, circular bore through
- Complex surface: Combination of curved and straight surfaces
- Surprising volume formula: V = π·L³/6 dependent on height L
- Radius dependency: Height L = 2√(R²-r²) determines all properties
- Rotational symmetry: Around the axis of the cylindrical bore
- Variable geometry: From thin ring to thick shell
Mathematical elegance
Surprising formulas
The volume formula V = π·L³/6 is surprisingly simple and depends only on height L, not directly on radii R and r.
Hybrid surface
The surface formula S = 2π·L·(r+R) elegantly considers both radii and shows the combination of inner and outer surfaces.
Practical relevance
In mechanical engineering and technology, the spherical ring offers optimal solutions for bearings, bushings, and hollow sphere constructions.
Geometric limits
The condition r < R defines the existence of the spherical ring; when r = R, the height L and thus the ring disappears.
Summary
The spherical ring embodies the perfect harmony between spherical and cylindrical geometry. As a solid sphere with cylindrical bore, it unites the natural elegance of the spherical form with the constructive clarity of cylindrical structures. Its mathematical properties - with the surprising volume formula π·L³/6 and the elegant surface calculation - make it a fascinating object of study in geometry. From technical applications in bearings and bushings to physical experiments with hollow spheres to architectural elements, the spherical ring offers versatile solutions for complex three-dimensional problems. It impressively demonstrates how the combination of different geometric basic forms leads to new, surprising mathematical relationships while combining both theoretical beauty and practical utility.
|
|
|
|