Spherical Sector Calculator
Online calculator and formulas for calculating a spherical sector
Spherical Sector Calculator
The Spherical Sector
The spherical sector is a cone-like section from the center of a sphere to its surface.
Spherical Sector Properties
The spherical sector: Combination of spherical segment and cone
Spherical Sector Visualization
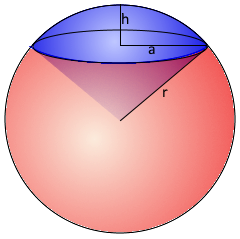
The Spherical Sector
Cone-like section from the center
Complete section from the center.
Combination of segment and cone.
|
|
What is a spherical sector?
The spherical sector is a special geometric shape:
- Definition: Cone-like section from the center of a sphere to its surface
- Structure: Combination of spherical segment and cone
- Completeness: Extends from center to sphere surface
- Feature: Unites curved and straight surfaces
- Application: Optics, geometry, architecture
- Relationship: Extends the spherical segment to the center
Geometric properties of the spherical sector
The spherical sector shows hybrid geometric properties:
Basic parameters
- Sphere radius r: Radius of the original solid sphere
- Segment height h: Height of the spherical segment portion
- Segment radius a: Radius of the circular cross-section
- Center point: Starting point of the cone-like extension
Special properties
- Hybrid form: Spherical segment plus cone surface
- Complete section: From center to surface
- Cone-like extension: Natural continuation to center
- Rotational symmetry: Around the axis through the center
Mathematical relationships of the spherical sector
The spherical sector follows extended mathematical laws:
Volume formula
The volume is proportional to r² and h. Simpler formula than the spherical segment.
Surface area formula
The surface area combines spherical cap and conical surface.
Applications of the spherical sector
Spherical sectors find applications in various fields:
Optics & Photonics
- Lens segments
- Reflectors
- Ray optics
- Lighting technology
Geodesy & Navigation
- Earth sphere sectors
- Coordinate systems
- Satellite navigation
- Surveying technology
Architecture & Design
- Special dome shapes
- Modern architecture
- Sculptural elements
- Interior design
Mathematics & Physics
- Volume calculations
- Integral calculus
- Geometric studies
- Spatial geometry
Formulas for the spherical sector
Sector Volume (Vs)
Volume of the cone-like sector
Segment Height (h)
Height from sphere and segment radius
Segment Radius (a)
Radius of the circular cross-section
Sphere Radius (r)
Reconstruction of the sphere radius
Cap Surface Area (Sc)
Curved surface area of the spherical cap
Cone Surface Area (SL)
Cone surface from center to cross-section
Sector Surface Area (S)
Spherical cap plus cone surface
Important difference from spherical segment
The spherical sector corresponds to a spherical segment that, instead of the flat base surface, has a cone-like continuation to the center of the sphere. This creates a complete, closed shape from the center to the sphere surface.
Calculation example for a spherical sector
Given
Find: All parameters of the spherical sector
1. Segment radius calculation
For r = 12 cm, h = 5 cm:
\[a = \sqrt{r^2 - (r - h)^2}\] \[a = \sqrt{144 - (12 - 5)^2}\] \[a = \sqrt{144 - 49} = \sqrt{95} ≈ 9.75 \text{ cm}\]The segment radius is approximately 9.75 cm
2. Sector volume calculation
With r = 12 cm, h = 5 cm:
\[V_s = \frac{2π \cdot r^2 \cdot h}{3}\] \[V_s = \frac{2π \cdot 144 \cdot 5}{3}\] \[V_s = \frac{1440π}{3} = 480π ≈ 1507.96 \text{ cm}^3\]The sector volume is approximately 1507.96 cm³
3. Cap surface calculation
With r = 12 cm, h = 5 cm:
\[S_c = 2π \cdot r \cdot h\] \[S_c = 2π \cdot 12 \cdot 5\] \[S_c = 120π ≈ 377.0 \text{ cm}^2\]The cap surface is approximately 377.0 cm²
4. Cone surface calculation
With a ≈ 9.75 cm, r = 12 cm:
\[S_L = π \cdot a \cdot r\] \[S_L = π \cdot 9.75 \cdot 12\] \[S_L = 117π ≈ 367.6 \text{ cm}^2\]The cone surface is approximately 367.6 cm²
5. Total surface calculation
Cap plus cone:
\[S = S_c + S_L\] \[S = 377.0 + 367.6\] \[S ≈ 744.6 \text{ cm}^2\]The total surface area is approximately 744.6 cm²
6. Summary
The spherical sector with 5 cm segment height
7. Comparison with spherical segment
V = 1507.96 cm³
V ≈ 1272.35 cm³
≈ 235.61 cm³
The sector has about 18.5% more volume than the segment due to the cone
8. Geometric analysis
h/r = 5/12 ≈ 0.42
a/r = 9.75/12 ≈ 0.81
Medium height
Wide base
With h/r ≈ 0.42, a balanced spherical sector with wide opening is formed
The Spherical Sector: Complete cone geometry
The spherical sector is a fascinating geometric shape that combines the elegance of the spherical segment with the completeness of a cone-like extension to the center. As a complete section from the center of a sphere to its surface, it shows the perfect synthesis between spherical curvature and conical geometry. Its mathematical properties - with the elegant volume formula V = 2πr²h/3 and the hybrid surface calculation - make it an ideal example for complex three-dimensional geometry. The spherical sector demonstrates how extending a known form creates new, practically relevant shapes.
The geometry of completeness
The spherical sector shows the perfection of complete sections:
- Cone-like extension: Natural continuation of the spherical segment to the center
- Hybrid surface: Combination of spherical cap and cone surface
- Complete shape: Closed form from center to surface
- Elegant mathematics: Simpler volume formula than the spherical segment
- Rotational symmetry: Perfect symmetry around the central axis
- Scalable geometry: From pointed cone to wide sectors
- Practical relevance: Important in optics, navigation and architecture
Mathematical elegance
Volume simplification
The volume formula V = 2πr²h/3 is more elegant than the spherical segment and shows direct proportionality to r² and h.
Surface hybridity
The combination of spherical cap (2πrh) and cone surface (πar) shows the dual nature of the sector.
Optical applications
In optics, spherical sectors enable precise beam guidance and light focusing through their cone-like geometry.
Geodetic significance
In geodesy, spherical sectors help calculate earth sphere sections and coordinate systems.
Summary
The spherical sector embodies the perfect completion of the spherical segment through its cone-like extension to the center. As a complete section from the center of a sphere to its surface, it unites the natural elegance of spherical curvature with the constructive clarity of conical geometry. Its mathematical properties - from the simplified volume formula to the hybrid surface calculation - demonstrate the beauty of extending geometry. From optical applications in lighting technology to geodetic calculations in surveying technology to architectural special solutions, the spherical sector shows its versatile applicability. It connects the purity of geometric forms with the functionality of complete shapes and remains an impressive example of the power of mathematical extensions in three-dimensional geometry.
|
|
|
|