Oloid Calculator
Calculator and formulas for calculating an oloid
Oloid Calculator
The Oloid
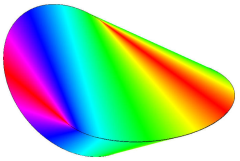
The oloid is the convex hull of two perpendicularly connected circles.
Oloid Properties
The oloid: Mathematical artwork with unique geometry
Oloid Visualization
Unique geometry with amazing properties.
Rolling body with constant width.
|
|
What is an oloid?
The oloid is an extraordinary geometric body:
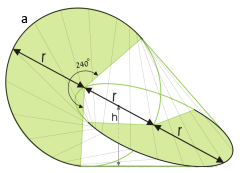
- Definition: Convex hull of two connected congruent circles in perpendicular planes
- Construction: Center of each circle lies on the edge of the other
- Distance: Circle centers are one radius apart from each other
- Peculiarity: One third of each circle's circumference lies in the convex hull
- Properties: Rolling body with constant width and unique shape
- Application: Art, design, mechanical applications
Geometric properties of the oloid
The oloid shows fascinating geometric properties:
Basic parameters
- Radius r: Radius of the two congruent circles
- Edge length a: 4π/3 × r - Circumference of the circular arcs
- Length l: 3r - Maximum extension
- Height h: 2r - Vertical extension
Special properties
- Convex hull: Smallest convex shape around both circles
- Rolling body: Rolls evenly on flat surfaces
- Constant width: Same extension in all directions
- Unique shape: Mathematically defined art form
Mathematical relationships of the oloid
The oloid follows exact mathematical laws:
Volume formula
The volume is determined by an irrational constant. Approximation value for practical calculations.
Surface area formula
The surface area equals that of a sphere with the same radius - remarkable property!
Applications of the oloid
Oloids find applications in various fields:
Art & Design
- Sculptural objects
- Modern art
- Design elements
- Architectural details
Mechanics & Engineering
- Rolling body applications
- Mixing equipment
- Transport mechanisms
- Precision mechanics
Education & Research
- Geometry teaching
- Mathematical studies
- Research objects
- Demonstrations
Toys & Games
- Educational toys
- Puzzle elements
- Physical games
- Collectibles
Formulas for calculating an oloid
Edge length (a)
Circumference of the circular arcs (4π/3 of the circle's circumference)
Length (l)
Maximum extension of the oloid
Height (h)
Vertical extension of the oloid
Surface area (S)
Equals the surface area of a sphere with radius r
Volume (V)*
*The volume is calculated using the irrational constant 3.0524184684... as an approximation. This constant is mathematically precisely defined, but cannot be represented by simple fractions or known constants.
Special mathematical property
Remarkably, the surface area of the oloid (S = 4πr²) exactly equals the surface area of a sphere with the same radius, even though the shapes are completely different. This shows the elegant mathematical structure of this extraordinary geometry.
Calculation example for an oloid
Given
Find: All parameters of the oloid
1. Edge length calculation
For r = 5 cm:
\[a = \frac{4π}{3} \cdot r\] \[a = \frac{4π}{3} \cdot 5\] \[a = \frac{20π}{3} ≈ 20.94 \text{ cm}\]The edge length is approximately 20.94 cm
2. Length calculation
With r = 5 cm:
\[l = 3 \cdot r = 3 \cdot 5\] \[l = 15 \text{ cm}\]The maximum length is 15 cm
3. Height calculation
With r = 5 cm:
\[h = 2 \cdot r = 2 \cdot 5\] \[h = 10 \text{ cm}\]The height is 10 cm
4. Surface area calculation
With r = 5 cm:
\[S = 4π \cdot r^2 = 4π \cdot 25\] \[S = 100π ≈ 314.16 \text{ cm}^2\]The surface area is approximately 314.16 cm²
5. Volume calculation
With r = 5 cm:
\[V = 3.0524184684 \cdot r^3\] \[V = 3.0524184684 \cdot 125\] \[V ≈ 381.55 \text{ cm}^3\]The volume is approximately 381.55 cm³
6. Summary
The oloid with radius 5 cm
7. Comparison with sphere
V = 381.55 cm³
S = 314.16 cm²
V = 523.60 cm³
S = 314.16 cm²
V: ≈ 72.9%
S: identical!
Remarkable: Same surface area as sphere, but 27% less volume
8. Geometric ratios
l/r = 15/5 = 3
h/r = 10/5 = 2
a/r = 4π/3 ≈ 4.19
Elongated ellipse
The oloid shows harmonic proportions with simple integer ratios
The Oloid: Mathematical artwork of geometry
The oloid is one of the most fascinating and at the same time most enigmatic geometric objects of modern mathematics. As the convex hull of two perpendicularly connected circles, it combines elegant construction logic with surprising mathematical properties. Its most remarkable property - the identical surface area with a sphere of the same radius despite completely different shape - makes it a true wonder of geometry. The oloid impressively demonstrates how complex and aesthetically appealing shapes can arise from simple basic elements, which possess both mathematical elegance and practical applicability.
The geometry of convexity
The oloid shows the beauty of convex hull geometry:
- Convex hull: Smallest convex shape that encloses both circles
- Perpendicular circles: Two congruent circles in rectangular planes
- Symmetric construction: Center of each circle on the edge of the other
- Rolling body properties: Even rolling on flat surfaces
- Constant width: Same extension in different directions
- Elegant proportions: Simple integer ratios (l=3r, h=2r)
- Unique aesthetics: Harmonic and organic design
Mathematical peculiarities
Surface area paradox
The surface area S = 4πr² is identical to a sphere - one of the most astonishing properties of geometry.
Irrational constant
The volume is determined by the irrational constant ≈3.0524 which cannot be expressed by simple formulas.
Rolling body mechanics
As a rolling body, the oloid shows unique mechanical properties for transport and mixing applications.
Construction elegance
The construction from only two circles leads to a shape of extraordinary mathematical and aesthetic complexity.
Summary
The oloid embodies the connection between mathematical precision and artistic beauty like hardly any other geometric body. As the convex hull of two perpendicularly connected circles, it shows how shapes of amazing complexity and elegance can arise from the simplest basic elements. Its paradoxical property - the identical surface area with a sphere despite completely different shape - makes it one of the most fascinating objects of modern geometry. From artistic sculptures to mechanical applications to mathematical research objects, the oloid shows its versatile significance. It connects the purity of geometric construction with the mystique of mathematical constants and remains a timeless symbol for the beauty and mystery of three-dimensional geometry.
|
|
|
|