Spherical Corner Calculator
Calculator and formulas for calculating spherical corners
Spherical Corner Calculator
The Spherical Corner
The spherical corner is a rectangular section from a hemisphere with characteristic geometric properties.
Spherical Corner Properties
The spherical corner: Rectangular section from a hemisphere
Spherical Corner Visualization
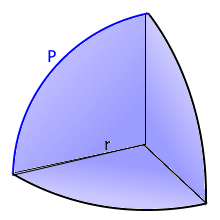
The Spherical Corner
Rectangular section from a hemisphere
Special geometry of the spherical corner.
Combination of straight and curved surfaces.
|
|
What is a spherical corner?
The spherical corner is a special geometric shape:
- Definition: Rectangular section from a hemisphere
- Shape: Combination of straight and curved surfaces
- Formation: Created by right-angled cuts in the hemisphere
- Application: Architecture, design, engineering
- Feature: Special surface area calculation
- Geometry: Unique volume/surface ratios
Geometric properties of the spherical corner
The spherical corner shows unique geometric properties:
Basic parameters
- Radius r: Fundamental determining parameter
- Arc length P: Length of the curved edges
- Rectangular base: Flat base surface
- Curved surface: Part of the original sphere
Special properties
- Hybrid shape: Straight and curved surfaces
- Special surface: Factor 5π/4 in surface calculation
- Unique volume: π/6 of the sphere radius³
- Architectural form: Common in modern design
Mathematical relationships of the spherical corner
The spherical corner follows special mathematical laws:
Volume formula
The volume is one-sixth of π × r³. Significantly smaller than a hemisphere.
Surface area formula
The surface area with factor 5π/4. Accounts for curved and flat surfaces.
Applications of the spherical corner
Spherical corners find applications in various fields:
Architecture & Design
- Modern building corners
- Interior architecture (niches)
- Sculptural elements
- Product design
Engineering
- Mechanical engineering (corner rounding)
- Tool design
- Fluid mechanics
- Container geometry
Art & Crafts
- Sculpture
- Ceramics and pottery
- Furniture design
- Jewelry making
Mathematics & Geometry
- Geometric studies
- Surface area calculation
- Volume optimization
- CAD applications
Formulas for calculating a spherical corner
Radius (r)
Radius from various parameters
Arc length (P)
Length of the curved edges
Surface area (S)
Total surface area including curved parts
Volume (V)
One-sixth of π × r³
Calculation example for a spherical corner
Given
Find: All parameters of the spherical corner
1. Arc length calculation
For r = 12 cm:
\[P = \frac{r \cdot \pi}{2} = \frac{12 \cdot \pi}{2}\] \[P = 6\pi ≈ 18.85 \text{ cm}\]The arc length is approximately 18.85 cm
2. Surface area calculation
With r = 12 cm:
\[S = \frac{5 \cdot \pi \cdot r^2}{4} = \frac{5 \cdot \pi \cdot 144}{4}\] \[S = \frac{720\pi}{4} = 180\pi\] \[S ≈ 565.49 \text{ cm}^2\]The surface area is approximately 565.49 cm²
3. Volume calculation
With r = 12 cm:
\[V = \frac{\pi \cdot r^3}{6} = \frac{\pi \cdot 1728}{6}\] \[V = \frac{1728\pi}{6} = 288\pi\] \[V ≈ 904.78 \text{ cm}^3\]The volume is approximately 904.78 cm³
4. Summary
The spherical corner with radius 12 cm
5. Comparison with other shapes
V = 904.78 cm³
V = 3619.11 cm³
V = 7238.23 cm³
The spherical corner has about 1/4 the volume of a hemisphere
The Spherical Corner: Special geometry between straight and curved
The spherical corner is a fascinating geometric shape that combines the elegance of curved surfaces with the precision of rectangular cuts. As a rectangular section from a hemisphere, it shows unique mathematical properties that make it interesting for both theoretical studies and practical applications. The spherical corner embodies the perfect harmony between the natural curvature of the sphere and the constructive clarity of rectangular geometry.
The geometry of the hybrid form
The spherical corner shows the fascination of geometric transitions:
- Rectangular base: Clear, flat base surface as starting point
- Curved surface: Preservation of the original sphere curvature
- Special edges: Transition between straight and curved areas
- Unique proportions: Volume π/6 r³, surface area 5π/4 r²
- Mathematical elegance: Simple formulas despite complex geometry
- Practical applicability: Ideal for architectural solutions
- Design potential: Versatile aesthetic possibilities
Mathematical specialties
Formula specialties
The spherical corner shows unique factors: 5π/4 for surface area and π/6 for volume - mathematical elegance in special form.
Geometric transitions
The connection of straight and curved surfaces creates interesting mathematical challenges in calculation.
Practical relevance
In architecture and design, the spherical corner offers optimal solutions for corner rounding and aesthetic transitions.
Constructive advantages
The combination of rectangular base and curved surface enables both constructive clarity and aesthetic elegance.
Summary
The spherical corner embodies the perfect synthesis between geometric clarity and natural curvature. As a rectangular section from a hemisphere, it connects the constructive precision of rectangular forms with the aesthetic elegance of curved surfaces. Its special mathematical properties - with the characteristic factors π/6 for volume and 5π/4 for surface area - make it a fascinating object of study in geometry. From modern architecture to product design to engineering applications, the spherical corner offers versatile solutions for the transition between straight and curved forms. It impressively demonstrates how mathematical precision and aesthetic beauty can be harmoniously united in a single geometric form.
|
|
|
|