Paraboloid Calculator
Calculator and formulas for calculating a paraboloid
Paraboloid Calculator
The Paraboloid
The paraboloid is a second-order surface, known from satellite dishes and reflectors.
Paraboloid Properties
The paraboloid: Perfect focusing through parabolic curvature
Paraboloid Visualization
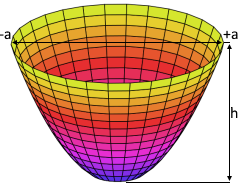
The Paraboloid
Paraboloid of revolution with perfect focusing
Perfect focusing of parallel rays.
Foundation of modern reflector technology.
|
|
What is a paraboloid?
The paraboloid is a fundamental geometric shape:
- Definition: Second-order surface created by rotating a parabola
- Properties: Focuses parallel rays at a focal point
- Shape: Bowl or dish-shaped surface
- Applications: Satellite dishes, reflectors, antennas
- Specialty: Perfect optical and acoustic properties
- Technology: Foundation of modern communication technology
Geometric properties of the paraboloid
The paraboloid shows unique geometric properties:
Basic parameters
- Shape parameter s: Determines the curvature of the parabola
- Radius a: Radius of the circular base
- Height h: h = s × a² - Dependent on shape and radius
- Rotational symmetry: Around the central axis
Special properties
- Focusing: Parallel rays meet at the focal point
- Reflection property: Perfect ray bundling
- Scalability: From flat to deep dishes
- Mathematical elegance: Defined by simple quadratic function
Mathematical relationships of the paraboloid
The paraboloid follows precise mathematical laws:
Volume formula
The volume is half of a cylinder with the same base and height.
Surface area formula
The surface area consists of lateral surface and circular base area.
Applications of the paraboloid
Paraboloids find applications in various fields:
Communication Technology
- Satellite dishes
- Radar antennas
- Radio telescopes
- Microwave antennas
Optics & Lighting
- Car headlights
- Searchlights
- Telescope mirrors
- Solar concentrators
Energy Technology
- Solar parabolic mirrors
- Solar collectors
- Thermal power plants
- Focusing systems
Architecture & Design
- Roof constructions
- Acoustic rooms
- Sculptural elements
- Modern architecture
Formulas for the paraboloid
Height (h)
Height determined by shape parameter and radius
Volume (V)
Half cylinder volume
Lateral surface (L)
Complex formula for curved surface
Surface area (S)
Lateral surface plus base circle
Parabolic equation
The basic equation of the paraboloid of revolution with shape parameter s determines the curvature of the parabolic surface. For s > 0, the parabola opens upward (concave shape).
Calculation example for a paraboloid
Given
Find: All parameters of the paraboloid
1. Height calculation
For s = 0.5, a = 4 cm:
\[h = s \cdot a^2\] \[h = 0.5 \cdot 16\] \[h = 8 \text{ cm}\]The height is 8 cm
2. Volume calculation
With a = 4 cm, h = 8 cm:
\[V = \frac{1}{2} \cdot π \cdot a^2 \cdot h\] \[V = \frac{1}{2} \cdot π \cdot 16 \cdot 8\] \[V = 64π ≈ 201.06 \text{ cm}^3\]The volume is approximately 201.06 cm³
3. Lateral surface calculation
With a = 4 cm, h = 8 cm:
\[a^2 + 4h^2 = 16 + 256 = 272\] \[\sqrt{272} ≈ 16.49\] \[L = \frac{π \cdot 4}{6 \cdot 64} \cdot (272^{3/2} - 64)\] \[L ≈ 84.85 \text{ cm}^2\]The lateral surface is approximately 84.85 cm²
4. Total surface area calculation
Base area + lateral surface:
\[A_{base} = π \cdot a^2 = π \cdot 16 ≈ 50.27 \text{ cm}^2\] \[S = L + A_{base}\] \[S = 84.85 + 50.27 ≈ 135.12 \text{ cm}^2\]The total surface area is approximately 135.12 cm²
5. Summary
The paraboloid with shape parameter 0.5
6. Comparison with cylinder
V = 201.06 cm³
V = 402.12 cm³
The paraboloid has exactly half the cylinder volume
7. Practical application: Satellite antenna
2a = 8 cm
h = 8 cm
Deep dish
Very good
With s = 0.5, a relatively deep parabolic dish with good focusing is created
8. Shape parameter analysis
Medium curvature
h/(2a) = 1.0
Universally usable
The shape parameter s = 0.5 creates a balanced parabolic shape
The Paraboloid: Perfection of focusing
The paraboloid is one of the most important and practically significant surfaces of analytical geometry. As a surface of revolution of a parabola, it combines mathematical elegance with extraordinary physical properties. Its most remarkable property - the perfect focusing of parallel rays at a single focal point - makes it the foundation of countless technical applications. From satellite dishes to car headlights to radio telescopes, modern technology uses the geometric perfection of the paraboloid. It impressively demonstrates how mathematical theory leads to practical solutions that shape our everyday life.
The geometry of focusing
The paraboloid shows the perfection of focusing geometry:
- Second-order surface: Defined by quadratic equation z = s(x²+y²)
- Rotational symmetry: Created by rotating a parabola around its axis
- Focusing property: All parallel rays meet at the focal point
- Shape parameter s: Determines curvature and thus focusing strength
- Scalability: From flat plates to deep dishes
- Mathematical elegance: Simple equation with complex properties
- Universal application: Optics, acoustics, electromagnetism
Technical significance
Communication technology
Satellite dishes and radar antennas use the focusing property for maximum signal strength and directivity.
Energy technology
Solar concentrators and parabolic mirrors bundle sunlight for efficient energy generation.
Optical systems
Telescopes and headlights use parabolic mirrors for perfect beam shaping and light collection.
Acoustic applications
Parabolic reflectors in microphones and speakers use focusing for optimal sound transmission.
Summary
The paraboloid embodies the perfect union of mathematical theory and technical practice. As a second-order surface, it shows how simple quadratic relationships can lead to extraordinary physical properties. Its focusing property - the perfect bundling of parallel rays at a focal point - makes it a fundamental building block of modern technology. From the satellite antenna on the roof to the headlight in the car to the radio telescope in research, countless applications use the geometric perfection of the paraboloid. It connects the elegance of mathematical forms with the power of physical laws and remains a timeless example of how geometry shapes and enables our technological world.
|
|
|
|