Torus Rechner
Rechner und Formeln zur Berechnung eines Torus
Torus Rechner
Der Torus
Der Torus ist eine donut-förmige Ringform mit Loch.
Torus Eigenschaften
Der Torus: Klassischer Donut mit charakteristischem Loch
Torus Visualisierung
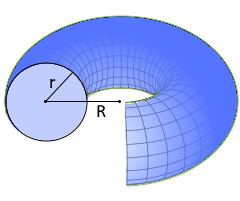
Torus Querschnitt
Zeigt die charakteristische Donut-Form
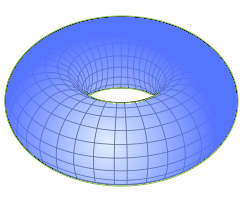
Torus 3D-Ansicht
Vollständige dreidimensionale Form
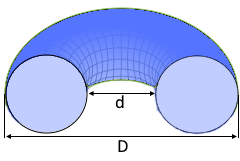
Torus Durchmesser
Große und kleine Durchmesser
Klassischer Donut mit Durchgangsloch.
Rotationskörper um zentrale Achse.
|
|
Was ist ein Torus?
Der Torus ist eine grundlegende geometrische Form:
- Definition: Rotationskörper, entstanden durch Rotation eines Kreises um eine Achse
- Form: Donut- oder Rettungsringform mit charakteristischem Durchgangsloch
- Parameter: Großer Radius R (Mittelpunkt bis Röhrenzentrum) und kleiner Radius r (Röhrenradius)
- Bedingung: R > r für klassischen Torus mit Loch
- Durchmesser: Großer Durchmesser D = 2(R+r), kleiner Durchmesser d = 2(R-r)
- Anwendung: Architektur, Maschinenbau, Mathematik, Design
Geometrische Eigenschaften des Torus
Der Torus zeigt charakteristische geometrische Eigenschaften:
Grundparameter
- Großer Radius R: Abstand vom Torus-Zentrum zum Röhrenmittelpunkt
- Kleiner Radius r: Radius der rotierenden Röhre
- Großer Durchmesser D: D = 2(R+r) - Außendurchmesser
- Kleiner Durchmesser d: d = 2(R-r) - Lochdurchmesser
Besondere Eigenschaften
- Durchgangsloch: Charakteristisches Loch in der Mitte
- Rotationssymmetrie: Symmetrisch um die zentrale Achse
- Donut-Form: Klassische wulstartige Ringgestalt
- Glatte Oberfläche: Keine Kanten oder Ecken
Mathematische Beziehungen des Torus
Der Torus folgt eleganten mathematischen Gesetzen:
Volumen-Formel
Das Volumen ist proportional zu R und r². Elegant durch π² charakterisiert.
Oberflächen-Formel
Die Oberfläche ist proportional zu R und r. Einfache lineare Beziehung zu beiden Radien.
Anwendungen des Torus
Tori finden Anwendung in verschiedenen Bereichen:
Architektur & Bau
- Moderne Gebäudearchitektur
- Kuppel- und Dachkonstruktionen
- Brückenelemente
- Skulpturale Bauwerke
Maschinenbau & Technik
- Dichtungsringe (O-Ringe)
- Reifen und Schläuche
- Rohrleitungssysteme
- Maschinenbauteile
Wissenschaft & Forschung
- Plasmaphysik (Tokamak-Reaktoren)
- Topologie und Mathematik
- Strömungsmechanik
- Materialwissenschaft
Design & Kunst
- Schmuckdesign
- Skulpturale Kunstwerke
- Produktdesign
- Möbeldesign
Formeln zum Torus
Volumen (V)
Volumen des Torus mit charakteristischem π²-Faktor
Oberfläche (S)
Gesamte Oberfläche des Torus
Großer Durchmesser (D)
Außendurchmesser des Torus
Kleiner Durchmesser (d)
Durchmesser des zentralen Lochs
Kleiner Radius (r)
Röhrenradius aus Durchmessern
Großer Radius (R)
Hauptradius aus Durchmesser und Röhrenradius
Torus Parametrisierung
Parametrische Darstellung mit u ∈ [0,2π] und v ∈ [0,2π]. Diese Gleichungen beschreiben jeden Punkt auf der Torus-Oberfläche.
Berechnungsbeispiele für einen Torus
Beispiel 1: Eingabe mit Radien
Gesucht: Alle Parameter des Torus
1. Durchmesser-Berechnung
Für R = 8 cm, r = 3 cm:
\[D = 2(R + r) = 2(8 + 3) = 22 \text{ cm}\] \[d = 2(R - r) = 2(8 - 3) = 10 \text{ cm}\]Außendurchmesser: 22 cm, Lochdurchmesser: 10 cm
2. Volumen-Berechnung
Mit R = 8 cm, r = 3 cm:
\[V = 2π^2 \cdot R \cdot r^2\] \[V = 2π^2 \cdot 8 \cdot 9\] \[V = 144π^2 ≈ 1421.3 \text{ cm}^3\]Das Volumen beträgt etwa 1421.3 cm³
3. Oberflächen-Berechnung
Mit R = 8 cm, r = 3 cm:
\[S = 4π^2 \cdot R \cdot r\] \[S = 4π^2 \cdot 8 \cdot 3\] \[S = 96π^2 ≈ 947.5 \text{ cm}^2\]Die Oberfläche beträgt etwa 947.5 cm²
4. Zusammenfassung Radien
Der klassische Torus mit Radius-Eingabe
Beispiel 2: Eingabe mit Durchmessern
5. Radius-Berechnung
Für D = 20 cm, d = 8 cm:
\[r = \frac{D - d}{4} = \frac{20 - 8}{4} = 3 \text{ cm}\] \[R = \frac{D}{2} - r = 10 - 3 = 7 \text{ cm}\]Großer Radius: 7 cm, kleiner Radius: 3 cm
6. Volumen aus Durchmessern
Mit R = 7 cm, r = 3 cm:
\[V = 2π^2 \cdot 7 \cdot 9\] \[V = 126π^2 ≈ 1243.6 \text{ cm}^3\]Das Volumen beträgt etwa 1243.6 cm³
7. Vergleich der Beispiele
R=8, r=3
V≈1421.3 cm³
R=7, r=3
V≈1243.6 cm³
ΔR=1 cm
ΔV≈177.7 cm³
Bei gleichem Röhrenradius r führt ein größerer Hauptradius R zu deutlich mehr Volumen
8. Praktische Anwendung: O-Ring
D = 22 mm
d = 10 mm
2r = 6 mm
≈ 1.42 cm³
Ein typischer O-Ring für industrielle Anwendungen mit berechneten Materialverbrauch
9. Mathematische Eigenschaften
π² ≈ 9.87
Torus-Charakteristikum
V/S = r/2
Elegante Beziehung
V ∝ R·r²
S ∝ R·r
Der Torus zeigt elegante mathematische Beziehungen mit dem charakteristischen π²-Faktor
Der Torus: Klassische Perfektion der Geometrie
Der Torus ist eine der elegantesten und praktisch bedeutsamsten Formen der dreidimensionalen Geometrie. Als Rotationskörper, entstanden durch die Rotation eines Kreises um eine Achse außerhalb des Kreises, verkörpert er mathematische Reinheit und praktische Vielseitigkeit in perfekter Harmonie. Seine charakteristische Donut-Form mit dem zentralen Durchgangsloch macht ihn nicht nur zu einem ästhetisch ansprechenden Objekt, sondern auch zu einer fundamentalen Struktur in Technik und Wissenschaft. Von einfachen O-Ringen über architektonische Meisterwerke bis hin zu hochmodernen Fusionsreaktoren zeigt der Torus seine universelle Anwendbarkeit und zeitlose geometrische Schönheit.
Die Geometrie der Rotation
Der Torus zeigt die Eleganz perfekter Rotationsgeometrie:
- Rotationsentstehung: Rotation eines Kreises um eine externe Achse
- Charakteristisches Loch: Natürliches Durchgangsloch durch Rotationsgeometrie
- Doppelte Krümmung: Sowohl in meridionaler als auch in äquatorialer Richtung
- π²-Eleganz: Charakteristischer π²-Faktor in Volumen- und Oberflächenformeln
- Parametrische Klarheit: Einfache Beziehungen zwischen allen Dimensionen
- Skalierungseigenschaften: V ∝ R·r², S ∝ R·r mit klaren Abhängigkeiten
- Topologische Bedeutung: Genus-1 Fläche in der algebraischen Topologie
Vielseitige Anwendungen
Technische Anwendungen
O-Ringe, Reifen und Schläuche nutzen die geschlossene Ringgeometrie für Dichtungs- und Transportfunktionen mit optimaler Materialverteilung.
Wissenschaftliche Bedeutung
In der Plasmaphysik ermöglichen toroidale Magnetfelder die Eindämmung von Fusionsplasmen in Tokamak-Reaktoren.
Architektonische Ästhetik
Moderne Architektur nutzt Torus-Formen für spektakuläre Gebäude, die Funktionalität mit visueller Wirkung verbinden.
Mathematische Schönheit
Als Standardbeispiel in der Differentialgeometrie und Topologie demonstriert der Torus fundamentale mathematische Konzepte.
Zusammenfassung
Der Torus verkörpert die perfekte Synthese zwischen mathematischer Eleganz und praktischer Funktionalität. Seine entstehung durch einfache Rotation eines Kreises führt zu einer Form von bemerkenswerter Vielseitigkeit und Schönheit. Die charakteristischen π²-Faktoren in seinen Formeln unterstreichen die tiefe mathematische Struktur dieser Geometrie. Von alltäglichen O-Ringen über architektonische Meisterwerke bis hin zu hochmodernen Fusionsreaktoren zeigt der Torus seine universelle Anwendbarkeit. Seine topologischen Eigenschaften als Genus-1 Fläche machen ihn zu einem fundamentalen Objekt der modernen Mathematik. Der Torus verbindet die Reinheit geometrischer Formen mit der Kraft praktischer Anwendungen und bleibt ein zeitloses Symbol für die Eleganz und Universalität mathematischer Strukturen in unserer physischen Welt.
|
|
|
|