Spindle Torus Calculator
Calculator and formulas for calculating a spindle torus
Spindle Torus Calculator
The Spindle Torus
The spindle torus is a torus type with indentation instead of hole.
Spindle Torus Properties
The spindle torus: Torus without through hole
Spindle Torus Visualization
Spindle Torus Cross Section
Shows the characteristic indentation
Spindle Torus 3D View
Complete three-dimensional form
Torus without through hole.
Characteristic spindle-shaped form.
|
|
What is a spindle torus?
The spindle torus is a special type of torus:
- Definition: Torus where the distance R is smaller than the tube radius r
- Characteristic: No through hole, only an indentation in the center
- Shape: Spindle-like, pear-shaped form
- Condition: R < r (distance smaller than tube radius)
- Formation: Rotation of a circle around an axis at small distance
- Application: Design, architecture, mechanical engineering
Geometric properties of the spindle torus
The spindle torus shows special geometric properties:
Basic parameters
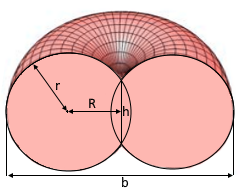
- Distance R: Distance from tube center to torus center
- Tube radius r: Radius of the rotating circle
- Condition: R < r for spindle torus formation
- Inner height h: h = 2√(r²-R²) - height of indentation
Special properties
- No hole: Closed unlike normal torus
- Indentation: Characteristic depression in the center
- Spindle shape: Pear or spindle-like overall form
- Rotational symmetry: Symmetric around the central axis
Mathematical relationships of the spindle torus
The spindle torus follows complex mathematical laws:
Inner height formula
The inner height depends on the ratio between tube radius and distance.
Volume formula
The volume requires integration over elliptic functions.
Applications of the spindle torus
Spindle tori find applications in various fields:
Design & Art
- Sculptural forms
- Modern architecture
- Product design
- Ceramics and pottery
Technology & Industry
- Pressure vessels
- Machine parts
- Fluid technology
- Process engineering
Architecture & Construction
- Dome constructions
- Bridge construction
- Tunnel construction
- Special building forms
Science & Research
- Topology studies
- Materials science
- Biomechanics
- Geometric analysis
Formulas for the spindle torus
Width (b)
Maximum width of the spindle torus
Inner Height (h)
Height of the central indentation
Volume (V)
Complex volume formula with elliptic integrals
Spindle Torus Condition
For the existence of a spindle torus must hold: R < r
If R ≥ r, a normal torus with hole or a ring torus is created.
At R = 0 results in a sphere with radius r.
Calculation example for a spindle torus
Given
Find: All parameters of the spindle torus
1. Check condition
For spindle torus: R < r
R = 3 cm, r = 5 cm
3 < 5 ✓ Condition fulfilled!
A spindle torus without hole is created
2. Width calculation
With R = 3 cm, r = 5 cm:
\[b = 2 \cdot (R + r)\] \[b = 2 \cdot (3 + 5)\] \[b = 2 \cdot 8 = 16 \text{ cm}\]The maximum width is 16 cm
3. Inner height calculation
With r = 5 cm, R = 3 cm:
\[h = 2 \cdot \sqrt{r^2 - R^2}\] \[h = 2 \cdot \sqrt{25 - 9}\] \[h = 2 \cdot \sqrt{16} = 2 \cdot 4 = 8 \text{ cm}\]The inner height of the indentation is 8 cm
4. Volume calculation (Part 1)
First term:
\[V_1 = \frac{2π}{3} \cdot (2r^2 + R^2) \cdot \sqrt{r^2 - R^2}\] \[V_1 = \frac{2π}{3} \cdot (50 + 9) \cdot 4\] \[V_1 = \frac{2π \cdot 59 \cdot 4}{3} ≈ 494.8 \text{ cm}^3\]First volume part calculated
5. Volume calculation (Part 2)
Second term with arctan:
\[\arctan\left(\frac{3}{4}\right) ≈ 0.6435 \text{ rad}\] \[V_2 = π \cdot 25 \cdot 3 \cdot (π + 2 \cdot 0.6435)\] \[V_2 ≈ 75π \cdot 4.4305 ≈ 1043.9 \text{ cm}^3\]Second volume part with elliptic integral
6. Total volume
Sum of both terms:
\[V = V_1 + V_2\] \[V ≈ 494.8 + 1043.9\] \[V ≈ 1538.7 \text{ cm}^3\]The total volume is approximately 1538.7 cm³
7. Summary
The spindle torus with characteristic indentation
8. Comparison with other shapes
V = 1538.7 cm³
No hole
V = 523.6 cm³
Compact
≈ 2.94× larger
Spindle shape
The spindle torus has almost three times the volume of a sphere with the same tube radius
9. Geometric analysis
3/5 = 0.6
h/b = 8/16 = 0.5
Medium indentation
Pronounced spindle
At R/r = 0.6 a clearly pronounced spindle shape without through hole is created
The Spindle Torus: Geometry without hole
The spindle torus is a fascinating geometric shape that occupies a special position in the family of torus shapes. As the only torus type without a through hole, it demonstrates how small parameter changes can lead to completely different geometric properties. The decisive condition R < r causes the rotating tube to overlap itself and form a characteristic indentation instead of a hole. This elegant shape finds attention not only in pure mathematics, but also in practical applications from architecture to mechanical engineering, where the combination of structural integrity and aesthetic appeal is valued.
The geometry of indentation
The spindle torus shows the elegance of closed torus geometry:
- Characteristic condition: R < r leads to self-overlap of the tube
- No through hole: Closed unlike the classical torus
- Central indentation: Characteristic depression with height h = 2√(r²-R²)
- Spindle shape: Pear or spindle-like overall form
- Maximum width: b = 2(R+r) - simple linear relationship
- Rotational symmetry: Perfect symmetry around the central axis
- Parameter continuity: Smooth transition to other torus forms
Mathematical complexity
Volume integration
The volume formula requires elliptic integrals and arctangent functions, which underlines the mathematical elegance of this form.
Geometric transitions
At R → 0 the spindle torus becomes a sphere, at R → r the transition to the classical torus occurs - continuous transformation.
Structural properties
The closed form without hole offers excellent structural integrity for technical applications.
Aesthetic effect
The organic, spindle-shaped form makes the spindle torus a preferred shape in design and architecture.
Summary
The spindle torus embodies the fascinating diversity of geometric forms that can arise from simple rotation principles. As the only torus without through hole, it shows how the variation of a parameter - the ratio R/r - leads to completely new geometric properties. Its characteristic indentation instead of a hole makes it not only mathematically interesting, but also practically valuable for applications that require structural closure. From sculptural artworks to architectural elements to technical components, the spindle torus shows its versatility. It connects the purity of mathematical definitions with the beauty of organic forms and remains an impressive example of how geometry can be both intellectually fascinating and aesthetically appealing.
|
|
|
|