Allgemeines Viereck berechnen

Rechner für beliebige Vierecke ohne spezielle Eigenschaften

Allgemeines Viereck Rechner

Allgemeines Viereck

Ein allgemeines Viereck ist die vielseitigste Viereck-Form mit beliebigen Seitenlängen und Winkeln.

Drei Seiten und zwei verbindende Winkel eingeben
Eingabe benötigt: 3 Seitenlängen (a, b, c) + 2 Winkel (β, γ) zur eindeutigen Bestimmung
Erste Seite
Zweite Seite
Dritte Seite
Winkel zwischen Seiten a und b
Winkel zwischen Seiten b und c
Allgemeines Viereck Ergebnisse
Seitenlänge d:
Diagonale e:
Diagonale f:
Flächeninhalt A:
Umfang U:
Winkel α:
Winkel δ:
Winkelsumme:
α + β + γ + δ = 360°

Allgemeines Viereck

Allgemeines Viereck Eigenschaften

Vielseitig: Keine speziellen Symmetrien, beliebige Seiten und Winkel

4 beliebige Seiten 4 beliebige Winkel Bretschneider-Formel

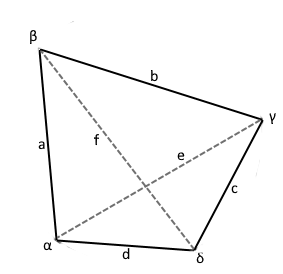
Allgemeines Viereck ohne spezielle Symmetrie.
Beliebige Seitenlängen und Winkel möglich.

Allgemeines Viereck

Das allgemeine Viereck: Vielseitigkeit ohne Einschränkungen

Das allgemeine Viereck ist die umfassendste Form der Viereck-Geometrie:

  • Beliebige Form: Keine speziellen Symmetrien oder Eigenschaften
  • Variable Seiten: Alle vier Seitenlängen können unterschiedlich sein
  • Flexible Winkel: Alle vier Winkel können variieren
  • Komplexe Berechnung: Erfordert Bretschneider-Formel
  • Eindeutige Bestimmung: 5 Parameter (3 Seiten + 2 Winkel)
  • Universelle Anwendung: Basis für alle Viereck-Arten

Geometrische Eigenschaften allgemeiner Vierecke

Die mathematischen Eigenschaften sind durch die Allgemeinheit geprägt:

Winkel-Eigenschaften
  • Winkelsumme: α + β + γ + δ = 360°
  • Keine speziellen Winkel-Beziehungen
  • Alle Winkel zwischen 0° und 180° möglich
  • Bestimmung über Kosinussatz und Geometrie
Seiten und Diagonalen
  • Alle vier Seiten können unterschiedlich sein
  • Diagonalen mit Kosinussatz berechenbar
  • Keine speziellen Diagonalen-Eigenschaften
  • Komplexe Beziehungen zwischen allen Parametern

Mathematik der allgemeinen Viereck-Berechnung

Die mathematische Behandlung verwendet fortgeschrittene Methoden:

Bretschneider-Formel
  • Verallgemeinerung der Brahmagupta-Formel
  • Berücksichtigt beliebige Winkel
  • Komplexer Ausdruck mit Winkelfunktionen
  • Fundamentale Flächenberechnung
Schrittweise Berechnung
  • Diagonalen über Kosinussatz
  • Vierte Seite über Hilfsdreiecke
  • Restliche Winkel über Kosinussatz
  • Fläche über Bretschneider-Formel

Anwendungen allgemeiner Vierecke

Allgemeine Vierecke sind omnipräsent in der realen Welt:

Vermessung & Geografie
  • Grundstücks-Vermessung und Kataster
  • Kartografie und Landvermessung
  • GPS-basierte Flächenbestimmung
  • Satelliten-Bildauswertung
Architektur & Bauwesen
  • Unregelmäßige Gebäude-Grundrisse
  • Dachkonstruktionen und Giebel
  • Landschaftsarchitektur
  • Stadtplanung und Parzellierung
Computergrafik & CAD
  • 3D-Modellierung und Mesh-Generierung
  • CAD-Software für technisches Zeichnen
  • Game Development und Level-Design
  • Finite-Elemente-Methoden
Ingenieurwesen
  • Maschinenbau-Komponenten
  • Strukturanalyse und Statik
  • Materialzuschnitt-Optimierung
  • Robotik und Bewegungsplanung

Formeln für das allgemeine Viereck

Diagonale e
\[e = \sqrt{a^2 + b^2 - 2ab \cos(\beta)}\]

Kosinussatz für Diagonale e aus Seiten a, b

Diagonale f
\[f = \sqrt{b^2 + c^2 - 2bc \cos(\gamma)}\]

Kosinussatz für Diagonale f aus Seiten b, c

Seitenlänge d
\[d = \sqrt{c^2 + e^2 - 2ce \cos(\gamma_2)}\]

Mit Hilfswinkel γ₂ = γ - γ₁

Umfang U
\[U = a + b + c + d\]

Summe aller vier Seitenlängen

Winkel α
\[\alpha = \arccos\left(\frac{a^2 + d^2 - f^2}{2ad}\right)\]

Kosinussatz rückwärts angewandt

Winkel δ
\[\delta = 360° - \alpha - \beta - \gamma\]

Winkelsumme im Viereck

Bretschneider-Flächenformel
\[A = \sqrt{(s-a)(s-b)(s-c)(s-d) - abcd \cos^2\left(\frac{\alpha + \gamma}{2}\right)}\] \[s = \frac{a + b + c + d}{2}\]

Verallgemeinerung der Brahmagupta-Formel für beliebige Vierecke

Rechenbeispiel für ein allgemeines Viereck

Gegeben
Seite a = 7 Seite b = 5 Seite c = 6 Winkel β = 80° Winkel γ = 70°

Gesucht: Alle fehlenden Parameter des allgemeinen Vierecks

1. Diagonalen berechnen
\[e = \sqrt{7^2 + 5^2 - 2 \times 7 \times 5 \times \cos(80°)} = 6.87\] \[f = \sqrt{5^2 + 6^2 - 2 \times 5 \times 6 \times \cos(70°)} = 6.04\]

Kosinussatz für beide Diagonalen

2. Vierte Seite d
\[\gamma_1 = \arccos\left(\frac{5^2 + 6.87^2 - 7^2}{2 \times 5 \times 6.87}\right) = 52.3°\] \[d = \sqrt{6^2 + 6.87^2 - 2 \times 6 \times 6.87 \times \cos(17.7°)} = 2.87\]

Mit Hilfswinkel γ₂ = 70° - 52.3° = 17.7°

3. Fehlende Winkel
α = arccos((49 + 8.24 - 36.48)/40.18) = 58.7°
δ = 360° - 58.7° - 80° - 70° = 151.3°

Kosinussatz und Winkelsumme

4. Vollständiges allgemeines Viereck
Seiten: a=7, b=5, c=6, d=2.87 Umfang U = 20.87 Diagonalen: e=6.87, f=6.04
Winkel: α=58.7°, β=80°, γ=70°, δ=151.3° Fläche A ≈ 26.8 (Bretschneider)

Vollständig bestimmtes allgemeines Viereck mit allen Parametern!

Das allgemeine Viereck: Universelle Geometrie ohne Grenzen

Das allgemeine Viereck steht als die umfassendste Form der Vierecks-Geometrie im Zentrum der modernen mathematischen Anwendungen. Ohne spezielle Symmetrien oder Einschränkungen verkörpert es die pure Vielseitigkeit geometrischer Formen und findet Anwendung überall dort, wo die reale Welt ihre unregelmäßigen, aber dennoch mathematisch beschreibbaren Strukturen zeigt. Von der Landvermessung über die Computergrafik bis zur Strukturanalyse bildet es die Grundlage für das Verständnis komplexer geometrischer Zusammenhänge.

Die mathematische Universalität

Das allgemeine Viereck demonstriert fundamentale geometrische Prinzipien:

  • Bretschneider-Formel: Verallgemeinerung der Brahmagupta-Formel für beliebige Vierecke
  • Kosinussatz-Anwendung: Systematische Berechnung von Diagonalen und fehlenden Seiten
  • Winkelsumme 360°: Fundamentale Eigenschaft aller ebenen Vierecke
  • Eindeutige Bestimmung: Fünf Parameter (3 Seiten + 2 Winkel) definieren alles
  • Trigonometrische Vollständigkeit: Alle Beziehungen über Sinus- und Kosinussatz
  • Geometrische Flexibilität: Basis für alle speziellen Viereck-Arten

Praktische Bedeutung in der realen Welt

Allgemeine Vierecke sind omnipräsent in praktischen Anwendungen:

Vermessung und Kartografie

Grundstücks-Grenzen folgen selten geometrischen Idealformen. Das allgemeine Viereck ermöglicht präzise Flächenberechnungen für Kataster und Landregister.

Architektur und Bauwesen

Moderne Architektur nutzt bewusst unregelmäßige Formen. Allgemeine Vierecke ermöglichen die mathematische Beschreibung innovativer Gebäude-Geometrien.

Computergrafik und CAD

3D-Modellierung basiert auf Polygonnetzen aus allgemeinen Vierecken. Jede komplexe Oberfläche lässt sich durch Viereck-Tessellierung approximieren.

Ingenieurwesen

Finite-Elemente-Methoden verwenden allgemeine Vierecke als Basis-Elemente für Strukturanalysen, Strömungssimulationen und Materialberechnungen.

Mathematische Herausforderungen und Lösungen

Die Behandlung allgemeiner Vierecke erfordert fortgeschrittene mathematische Methoden:

  • Bretschneider-Formel (1842): Historische Erweiterung der Brahmagupta-Formel
  • Komplexe Trigonometrie: Systematische Anwendung von Kosinussatz und Hilfswinkeln
  • Numerische Stabilität: Präzise Berechnung auch bei extremen Seitenverhältnissen
  • Algorithmische Effizienz: Optimierte Berechnungsreihenfolge für CAD-Systeme
  • Fehleranalyse: Behandlung von Rundungsfehlern und numerischen Instabilitäten
  • Geometrische Validierung: Prüfung auf Konstruierbarkeit und physikalische Sinnhaftigkeit

Zukunftsperspektiven und moderne Entwicklungen

Das allgemeine Viereck bleibt relevant für zukünftige Technologien:

Künstliche Intelligenz

Machine Learning Algorithmen für Geometrie-Erkennung und -Klassifikation basieren auf allgemeinen Viereck-Eigenschaften. Computer Vision nutzt diese für Objekterkennung.

Digitale Zwillinge

Präzise 3D-Modelle realer Objekte erfordern exakte Geometrie-Berechnungen. Allgemeine Vierecke sind fundamental für digitale Repräsentationen.

Robotik und Automation

Roboter-Navigation in unstrukturierten Umgebungen erfordert das Verständnis beliebiger geometrischer Formen und deren mathematische Beschreibung.

Nachhaltiges Design

Optimierte Materialnutzung erfordert präzise Flächenberechnungen unregelmäßiger Formen. Allgemeine Vierecke minimieren Verschnitt und Abfall.

Zusammenfassung

Das allgemeine Viereck steht als mathematisches Fundament für die Beschreibung beliebiger vierseitiger Formen ohne spezielle Einschränkungen. Seine universelle Anwendbarkeit - von der Bretschneider-Formel über trigonometrische Beziehungen bis hin zu modernen CAD-Systemen - macht es zu einem unverzichtbaren Werkzeug der angewandten Mathematik. In einer Welt zunehmend komplexer Geometrien, von Architektur über Computergrafik bis zu KI-gestützten Systemen, bleibt das Verständnis allgemeiner Vierecke fundamental für Ingenieure, Architekten, Programmierer und Wissenschaftler. Es erinnert uns daran, dass mathematische Eleganz nicht nur in perfekten Symmetrien liegt, sondern auch in der Fähigkeit, das Unregelmäßige präzise zu beschreiben und zu verstehen.

Weitere Viereck Funktionen

Quadrat • Rechteck • Goldenes Rechteck • Rechteck und Quadrat • Parallelogramm • Parallelogramm Flächeninhalt • Raute • Raute Flächeninhalt • Allgemeines Viereck • Sehnenviereck • Konkaves Viereck • Pfeilviereck • Überschlagenes Viereck • Rahmen • Drachenviereck • Drachenviereck Flächeninhalt • Drachenviereck, Halbquadrat • Drachenviereck, rechtwinklig