Goldenes Rechteck berechnen
Rechner und Formeln für das göttliche Verhältnis φ ≈ 1.618
Goldenes Rechteck Rechner
Das Goldene Rechteck
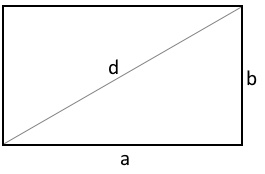
Ein Goldenes Rechteck hat ein Seitenverhältnis des Goldenen Schnitts: φ = (a + b) / a = a / b ≈ 1.618.
Goldenes Rechteck
Der Goldene Schnitt φ
Besonderheit: Das göttliche Verhältnis in Natur, Kunst und Architektur
Das Goldene Rechteck mit dem perfekten Verhältnis φ ≈ 1.618.
Harmonische Proportionen in reinster Form.
|
|
Das Goldene Rechteck und der Goldene Schnitt
Das Goldene Rechteck verkörpert das harmonischste aller Seitenverhältnisse:
- Göttliches Verhältnis: φ = (1 + √5) / 2 ≈ 1.618033988
- Goldener Schnitt: (a + b) / a = a / b = φ
- Perfekte Harmonie: Natürlich ansprechende Proportionen
- Universelle Konstante: In Natur, Kunst und Architektur
- Fibonacci-Beziehung: Limes der Fibonacci-Quotienten
- Optimale Ästhetik: Wissenschaftlich belegte Schönheit
Die Mathematik des Goldenen Schnitts φ
Der Goldene Schnitt besitzt einzigartige mathematische Eigenschaften:
Fundamentale Gleichung
- φ² = φ + 1 (einzigartige Eigenschaft)
- φ = (1 + √5) / 2 ≈ 1.618033988
- 1/φ = φ - 1 ≈ 0.618033988
- φ + 1/φ = √5 ≈ 2.236067977
Fibonacci-Verbindung
- lim(F(n+1)/F(n)) = φ (n→∞)
- F(n) = (φⁿ - (-φ)⁻ⁿ) / √5
- Fortsetzende Bruchentwicklung: [1; 1, 1, 1, ...]
- Langsamste Konvergenz aller irrationalen Zahlen
Goldenes Rechteck in Kunst und Architektur
Das Goldene Rechteck inspiriert Künstler und Architekten seit Jahrtausenden:
Architektur-Meisterwerke
- Parthenon: Fassade im Goldenen Rechteck
- Pyramiden von Gizeh: φ-Proportionen
- Notre-Dame de Paris: Hauptportal-Geometrie
- Taj Mahal: Gesamtproportionen und Details
Kunst-Meisterwerke
- Leonardo da Vinci: Mona Lisa, Vitruvianischer Mensch
- Sandro Botticelli: Geburt der Venus
- Salvador Dalí: Das Abendmahl (bewusste φ-Nutzung)
- Georges Seurat: Bathers at Asnières
Moderne Anwendungen des Goldenen Rechtecks
Das Goldene Rechteck findet heute vielfältige praktische Anwendungen:
Design & Medien
- Website-Layouts und Benutzeroberflächen
- Logos und Corporate Design
- Buchformate und Seitenlayouts
- Fotografie-Komposition
Produktdesign
- Smartphone- und Tablet-Proportionen
- Automobildesign (Karosserie-Verhältnisse)
- Möbeldesign und Innenarchitektur
- Verpackungsdesign und Marketing
Natur & Biologie
- Blütenblatt-Anordnungen (Fibonacci-Spiralen)
- Nautilus-Schneckenhaus (logarithmische Spirale)
- Menschliche Körperproportionen
- DNA-Doppelhelix-Geometrie
Finanzwelt & Technik
- Fibonacci-Retracements im Trading
- Optimierungsalgorithmen
- Architektur-Software und CAD
- KI und maschinelles Lernen
Formeln für das Goldene Rechteck
Goldener Schnitt φ
Die fundamentale Konstante der Harmonie
Seitenlänge b
Kürzere Seite aus längerer berechnet
Seitenlänge a (aus verschiedenen Parametern)
Längere Seite aus verschiedenen Parametern
Diagonale d
Pythagoras mit φ-Beziehung
Umfang U
Mit φ-Verhältnis optimiert
Flächeninhalt A
Elegant mit φ-Division
Besondere φ-Eigenschaften
Einzigartige mathematische Beziehungen
Rechenbeispiel für ein Goldenes Rechteck
Gegeben
Gesucht: Alle Parameter des Goldenen Rechtecks
1. φ-Konstante anwenden
Kürzere Seite mit Goldenem Schnitt
2. Umfang und Fläche
Grundlegende Rechteck-Formeln
3. Diagonale berechnen
Klassischer Pythagoras mit φ-Proportionen
4. Vollständiges Goldenes Rechteck
Das perfekte Goldene Rechteck - göttliche Proportionen in reinster Form!
Das Goldene Rechteck: Harmonie zwischen Mathematik und Ästhetik
Das Goldene Rechteck verkörpert die perfekte Verschmelzung von mathematischer Präzision und ästhetischer Harmonie. Mit dem Seitenverhältnis des Goldenen Schnitts φ ≈ 1.618 repräsentiert es eine der fundamentalsten Proportionen in Natur, Kunst und Architektur und demonstriert, wie mathematische Konstanten zu zeitloser Schönheit führen können.
Der Goldene Schnitt: Eine mathematische Konstante mit ästhetischer Wirkung
Die Besonderheit des Goldenen Schnitts liegt in seinen einzigartigen mathematischen Eigenschaften:
- Selbstreferenz: φ² = φ + 1 (die einzige Zahl mit dieser Eigenschaft)
- Kontinuierlicher Bruch: φ = [1; 1, 1, 1, 1, ...] (einfachste Form)
- Fibonacci-Grenzwert: lim(F(n+1)/F(n)) = φ für n→∞
- Algebraische Wurzel: φ = (1 + √5)/2 aus der Gleichung x² - x - 1 = 0
- Reziprok-Beziehung: 1/φ = φ - 1 ≈ 0.618 (einzigartige Eigenschaft)
- Pentagram-Geometrie: Grundlage der Pentagon- und Pentagramm-Konstruktion
Das Goldene Rechteck in der Natur
Die Natur nutzt das φ-Verhältnis zur Optimierung von Wachstum und Struktur:
Botanische Spiralen
Sonnenblumen, Tannenzapfen und Ananas zeigen Fibonacci-Spiralen, deren Verhältnis gegen φ konvergiert. Diese Anordnung maximiert die Platzeffizienz.
Anatomische Proportionen
Der menschliche Körper zeigt φ-Verhältnisse: Gesamthöhe zu Nabelhöhe, Fingergliedlängen und Gesichtsproportionen folgen oft dem Goldenen Schnitt.
Nautilus und Spiralen
Das Nautilus-Schneckenhaus wächst nach einer logarithmischen Spirale, deren Wachstumsfaktor mit φ verwandt ist - optimale Raum- und Materialnutzung.
DNA-Struktur
Die Doppelhelix-Geometrie der DNA zeigt φ-Beziehungen: Ein kompletter Windungszyklus entspricht annähernd φ-Proportionen.
Meisterwerke der Kunst und Architektur
Das Goldene Rechteck inspiriert Künstler und Architekten seit der Antike:
- Parthenon-Tempel: Die Gesamtproportionen der Fassade bilden ein nahezu perfektes Goldenes Rechteck
- Leonardo da Vinci: Der Vitruvianische Mensch und die Mona Lisa nutzen φ-Proportionen für harmonische Komposition
- Salvador Dalí: "Das Abendmahl" wurde bewusst im Goldenen Rechteck komponiert
- Notre-Dame de Paris: Hauptportal und Westfassade zeigen φ-Verhältnisse
- Moderne Architektur: Le Corbusiers "Modulor" basiert auf φ-Proportionen
- Designgeschichte: Von Apple-Produkten bis zu VW-Käfer - φ prägt erfolgreiches Design
Moderne Anwendungen und Technologie
Das φ-Verhältnis findet heute vielfältige technische Anwendungen:
User Interface Design
Webseiten, Apps und Software nutzen φ-Proportionen für intuitive und ästhetisch ansprechende Layouts. Das "goldene Layout" ist ein UI/UX-Standard.
Finanzmarkt-Analyse
Fibonacci-Retracements mit φ-Verhältnissen sind wichtige Werkzeuge der technischen Analyse für Trader und Investoren.
Produktdesign
Smartphones, Tablets, Kreditkarten und unzählige Konsumprodukte verwenden φ-Proportionen für optimale Ergonomie und Ästhetik.
Algorithmen und KI
Der Golden Section Search ist ein effizienter Optimierungsalgorithmus. Machine Learning nutzt φ-basierte Strukturen für neuronale Netzwerke.
Psychologie der Schönheit: Warum φ funktioniert
Wissenschaftliche Studien zeigen, warum das φ-Verhältnis als besonders schön empfunden wird:
- Neurologische Resonanz: Das Gehirn verarbeitet φ-Proportionen besonders effizient
- Evolutionäre Prägung: Präferenz für natürliche Proportionen ist angeboren
- Visuelle Balance: φ schafft optimale Spannung zwischen Symmetrie und Asymmetrie
- Kulturelle Universalität: φ-Präferenz ist kulturübergreifend nachweisbar
- Aufmerksamkeits-Optimum: φ-Layouts lenken den Blick optimal durch Inhalte
- Erinnerungs-Enhancement: φ-strukturierte Inhalte werden besser behalten
Zusammenfassung
Das Goldene Rechteck steht als zeitloses Symbol für die Einheit von Mathematik, Natur und Ästhetik. Der Goldene Schnitt φ ist mehr als nur eine mathematische Konstante - er ist ein universelles Prinzip der Harmonie, das von der molekularen Ebene bis zu architektonischen Meisterwerken wirkt. In unserer digitalen Zeit gewinnt φ neue Relevanz: von User Interface Design über Algorithmus-Optimierung bis zu KI-Strukturen. Das Goldene Rechteck erinnert uns daran, dass wahre Schönheit nicht willkürlich ist, sondern mathematischen Gesetzmäßigkeiten folgt. Es zeigt, dass die perfekte Balance zwischen Ordnung und Dynamik, zwischen Vorhersagbarkeit und Überraschung, in einer einfachen Zahl ausgedrückt werden kann: φ ≈ 1.618 - das göttliche Verhältnis, das Natur und Kultur gleichermaßen inspiriert und leitet.
|
|
|
|