Raute berechnen
Rechner und Formeln für das gleichseitige Rhombus
Raute Rechner
Die Raute (Rhombus)
Eine Raute ist ein gleichseitiges Viereck mit vier gleichen Seiten und parallelen Gegenseiten.
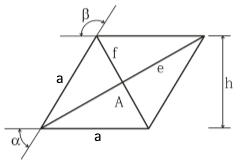
Raute Struktur
Raute Eigenschaften
Spezialfall: Alle Seiten gleich, gegenüberliegende Winkel gleich
Raute mit vier gleichen Seiten a.
Diagonalen stehen senkrecht aufeinander.
|
|
Die Raute: Diamantförmige Perfektion der Gleichseitigkeit
Die Raute (Rhombus) vereint die Eigenschaften eines Parallelogramms mit vier gleichen Seiten:
- Vier gleiche Seiten: |a| = |b| = |c| = |d|
- Parallelität: Gegenüberliegende Seiten parallel
- Supplementwinkel: α + β = 180° (benachbarte Winkel)
- Gleiche Gegenwinkel: α = γ und β = δ
- Senkrechte Diagonalen: e ⟂ f im Mittelpunkt
- Doppelte Flächenformel: A = a×h = (e×f)/2
Besondere Geometrie der Raute
Die geometrischen Eigenschaften der Raute sind einzigartig unter den Vierecken:
Diagonalen-System
- Diagonalen stehen senkrecht aufeinander (e ⟂ f)
- Diagonalen halbieren sich im Mittelpunkt
- Diagonalen halbieren die Innenwinkel
- Flächenformel: A = (e × f) / 2
Winkel-Eigenschaften
- Gegenüberliegende Winkel sind gleich (α = γ)
- Benachbarte Winkel ergänzen sich (α + β = 180°)
- Höhe h = a × sin(α) = a × sin(β)
- Zwei Symmetrieachsen (die Diagonalen)
Mathematik der Rauten-Berechnung
Die mathematischen Beziehungen der Raute nutzen Trigonometrie und Geometrie:
Trigonometrische Beziehungen
- Höhe: h = a × sin(α) = a × sin(β)
- Fläche: A = a² × sin(α)
- Diagonalen mit Cosinus-Formeln
- Winkel aus Höhe: α = arcsin(h/a)
Diagonalen-Berechnung
- Seitenlänge: a = √((e/2)² + (f/2)²)
- e = 2a × cos(α/2), f = 2a × cos(β/2)
- Höhen-Beziehung: e = h/sin(α/2)
- Pythagorischer Satz für Diagonalen
Anwendungen der Raute
Rauten finden vielfältige Anwendungen in Natur, Kunst und Technik:
Kristalle & Mineralien
- Diamant-Kristallstruktur
- Rhombische Kristallsysteme
- Kalkspat und andere Mineralien
- Molekulare Gitterstrukturen
Design & Kunst
- Diamant-Logo-Design
- Rhombische Muster und Ornamente
- Textile Designs (Argyle-Muster)
- Architektonische Fliesengestaltung
Technik & Konstruktion
- Parallelogramm-Lenker in Fahrzeugen
- Streckmetall und Gitterstrukturen
- Fachwerk-Konstruktionen
- Mechanische Getriebe-Systeme
Spiele & Symbole
- Spielkarten-Karo (Diamant)
- Verkehrszeichen-Geometrie
- Baseball-Diamant (Spielfeld)
- Warnzeichen und Piktogramme
Formeln für die Raute
Flächeninhalt A
Drei Berechnungsweisen für die Fläche
Seitenlänge a
Aus Fläche/Höhe oder Diagonalen
Höhe h
Höhe aus Fläche oder trigonometrisch
Umfang P
Vier gleiche Seiten
Diagonale e
Längere Diagonale
Diagonale f
Kürzere Diagonale
Winkel-Beziehungen
Supplementäre Winkel und trigonometrische Berechnung
Rechenbeispiel für eine Raute
Gegeben
Gesucht: Alle Parameter der Raute
1. Grundparameter berechnen
Fläche und Umfang direkt berechenbar
2. Winkel bestimmen
Trigonometrische Winkel-Berechnung
3. Diagonalen berechnen
Cosinus-Formeln für beide Diagonalen
4. Vollständige Raute
Vollständige Raute mit diamantförmiger Eleganz!
Die Raute: Diamantförmige Perfektion zwischen Quadrat und Parallelogramm
Die Raute (Rhombus) vereint als gleichseitiges Parallelogramm die Eigenschaften von Parallelität und gleichlangen Seiten zu einer einzigartigen geometrischen Form. Als Diamant in Spielkarten, als Kristallstruktur in der Natur oder als elegantes Gestaltungselement in der Architektur - die Raute fasziniert durch ihre perfekte Balance zwischen Symmetrie und Dynamik, zwischen Stabilität und visueller Bewegung.
Die mathematische Eleganz der Raute
Die Raute illustriert faszinierende geometrische Prinzipien:
- Doppelte Identität: Parallelogramm mit vier gleichen Seiten
- Senkrechte Diagonalen: e ⊥ f - einzigartig unter Parallelogrammen
- Doppelte Flächenformel: A = a×h = (e×f)/2 - zwei Berechnungswege
- Trigonometrische Vollständigkeit: Alle Parameter aus zwei Werten berechenbar
- Winkel-Symmetrie: α + β = 180°, α = γ, β = δ
- Diagonalen-Halbierung: Mittelpunkt teilt beide Diagonalen
Die Raute in Natur und Kristallographie
In der Natur manifestiert sich die Raute in beeindruckender Vielfalt:
Kristallsysteme
Das rhombische Kristallsystem zeigt Rauten-Strukturen in drei Dimensionen. Kalkspat, Gips und viele andere Mineralien kristallisieren in rhombischen Formen.
Molekulare Geometrie
Benzol-Ringe und andere organische Verbindungen zeigen rhombische Symmetrien. Die Diamant-Kristallstruktur basiert auf rhombischen Bausteinen.
Biologische Strukturen
Waben-Strukturen, Schuppen-Anordnungen und pflanzliche Muster nutzen rhombische Geometrien für optimale Raumausnutzung.
Geologie
Basalt-Säulen, Sediment-Schichtungen und tektonische Strukturen zeigen oft rhombische Bruchmuster und Symmetrien.
Kulturelle und symbolische Bedeutung
Die Raute trägt tiefe kulturelle und symbolische Bedeutungen:
- Spielkarten-Symbolik: Karo (Diamant) als Symbol für Reichtum und Materialität
- Heraldische Tradition: Rauten in Wappen symbolisieren Adel und Würde
- Textil-Design: Argyle-Muster und rhombische Ornamente in schottischen Traditionen
- Verkehrs-Symbolik: Rhombische Warnschilder für erhöhte Aufmerksamkeit
- Religiöse Symbolik: Rauten als Symbole der Erdverbundenheit und Stabilität
- Moderne Ästhetik: Diamant-Logos als Zeichen für Qualität und Exklusivität
Technische Anwendungen der Rhombus-Geometrie
Ingenieurswesen und Technik nutzen Rauten-Strukturen für optimale Funktionalität:
Mechanische Systeme
Parallelogramm-Lenker in Fahrzeugen nutzen Rauten-Geometrie für gleichmäßige Kraftübertragung. Scherenhubtische verwenden rhombische Mechaniken.
Strukturelle Anwendungen
Streckmetall und expandierte Gitter nutzen Rauten-Muster für optimale Festigkeit bei minimalem Materialverbrauch.
Optische Systeme
Prisma-Arrays und optische Gitter verwenden rhombische Anordnungen für Lichtbrechung und -dispersion.
Elektronik
Antenne-Arrays und Sensornetzwerke nutzen rhombische Geometrien für optimale Feldabdeckung und Signalverteilung.
Zukunftsperspektiven der Rauten-Geometrie
Moderne Technologien erschließen neue Anwendungsfelder für Rauten-Strukturen:
- Metamaterialien: Rhombische Unit Cells für exotische optische Eigenschaften
- Nanotechnologie: Molekulare Rauten als Bausteine für Nanomaschinen
- Smart Materials: Adaptive Strukturen mit variabler Rhombus-Geometrie
- Robotik: Rhombische Roboter-Konfigurationen für optimale Beweglichkeit
- Architektur 4.0: Responsive Fassaden mit dynamischen Rauten-Mustern
- Quantencomputing: Rhombische Qubit-Anordnungen für Fehlerkorrektur
Zusammenfassung
Die Raute steht als diamantförmiges Symbol für geometrische Eleganz und mathematische Vollständigkeit. Als gleichseitiges Parallelogramm vereint sie Symmetrie mit Dynamik, Stabilität mit visueller Bewegung. Ihre einzigartigen Eigenschaften - senkrechte Diagonalen, doppelte Flächenformeln und trigonometrische Vollständigkeit - machen sie zu einem faszinierenden Studienobjekt der Geometrie. Von der Kristallstruktur des Diamanten über kulturelle Symbole bis hin zu modernen technischen Anwendungen bleibt die Raute ein zeitloses Beispiel dafür, wie mathematische Perfektion und praktische Funktionalität in harmonischer Einheit verschmelzen. Sie erinnert uns daran, dass wahre Schönheit oft in der perfekten Balance liegt - vier gleiche Seiten, die unendliche Möglichkeiten eröffnen.
|
|
|
|